矩陣條件數學習[轉載]
阿新 • • 發佈:2018-11-28
轉自:https://baike.baidu.com/item/%E7%9F%A9%E9%98%B5%E6%9D%A1%E4%BB%B6%E6%95%B0/10150161?fr=aladdin
https://wenku.baidu.com/view/27cc784a02768e9951e738ff.html
1.定義
矩陣A的條件數等於A的範數與A的逆的範數的乘積,即cond(A)=‖A‖·‖A^(-1)‖,對應矩陣的3種範數,相應地可以定義3種條件數。 函式 cond(A,1)、cond(A)或cond(A inf) 是判斷矩陣病態與否的一種度量,條件數越大矩陣越病態。
作用:表示了矩陣計算對於誤差的敏感性
2.例子
條件數事實上表示了矩陣計算對於誤差的敏感性。對於線性方程組Ax=b,如果A的條件數大,b的微小改變就能引起解x較大的改變,數值穩定性差。如果A的條件數小,b有微小的改變,x的改變也很微小,數值穩定性好。它也可以表示b不變,而A有微小改變時,x的變化情況。 比如線性方程組 的解是(x,y)=(0.0,0.1),
而
的解是(x,y)=(0.0,0.1),
而

的解是(x,y)=(-0.17,0.22)
可見b很小的擾動就引起了x很大的變化,這就是A矩陣條件數大的表現。
一個極端的例子,當A奇異時,條件數為無窮,這時即使不改變b,x也可以改變。奇異的本質原因在於矩陣有0特徵值,x在對應特徵向量的方向上運動不改變Ax的值。如果一個特徵值比其它特徵值在數量級上小很多,x在對應特徵向量方向上很大的移動才能產生b微小的變化,這就解釋了為什麼這個矩陣為什麼會有大的條件數。
事實上,正規陣在二範數下的條件數就可以表示成 abs(最大特徵值/最小特徵值)。
3.例子2


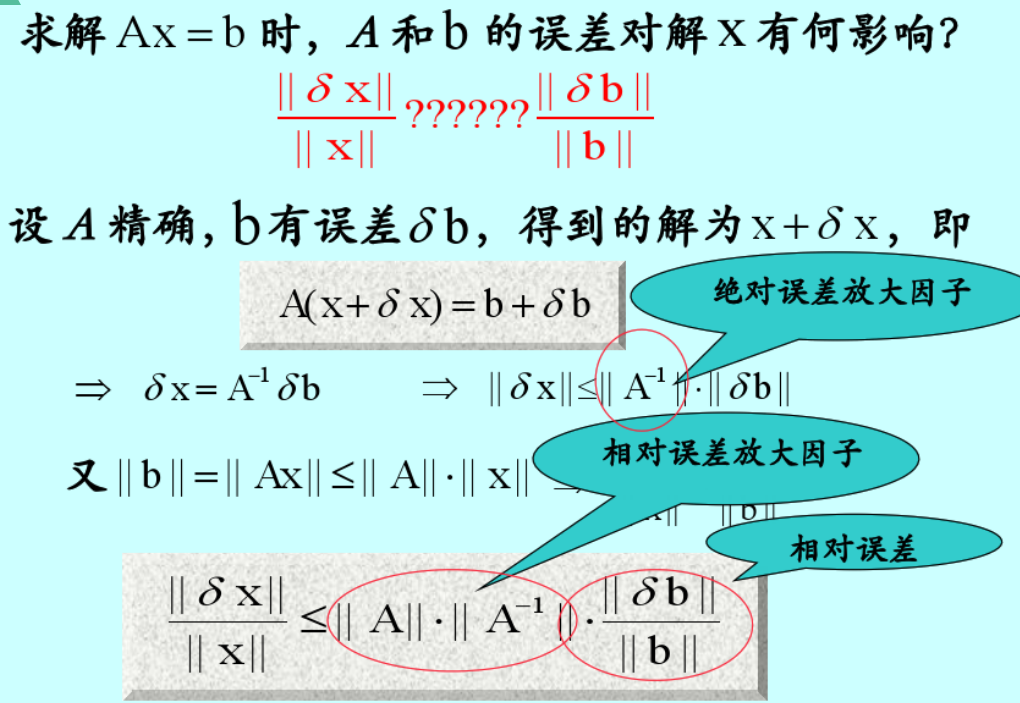
上圖中的推導過程還是比較容易理解的,能夠推匯出這個條件數的公式——圖中的相對誤差放大因子。
4.常用條件數

其中無窮(最大)範數是指取矩陣中的max值:
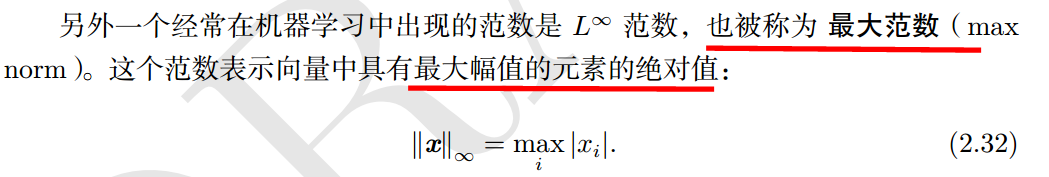
5.病態方程的數值例子

之後有給出了一個證明,對於條件數≈1的,基本上A和b的擾動對於解x沒有很大的影響,可以忽略,即對於非奇異矩陣。
對於奇異矩陣來說,擾動是非常大的,是病態矩陣。
