深入理解浮點數有效位
https://blog.csdn.net/dreamer2020/article/details/24158303/
平時接觸C及Java較多,這種層次的語言對資料的表示有一定侷限。基本的資料型別無外呼整數和浮點數。整數好說,一般僅需考慮越界問題。但對於浮點數,除了範圍外,通常很容易忽略精度問題。
浮點數為什麼會有精度問題?計算機中的浮點數對應於數學當中的小數。簡單計算下,32位浮點數最多可以表示2^32個數,但從數學上說區間[0,1]中的小數就有無窮多個。所以計算機是不可能描述得盡的,必然會有一些近似,也就帶來了精度損失。
所以在使用計算機中的浮點數之前,我們先要搞清楚計算機表示小數有多準。
浮點數標準
考慮這個問題,首先要知道浮點數在計算機中是怎麼表示的。當前,計算機中浮點數採用的是IEEE 754標準。浮點數分為單精度浮點數(32位)和雙精度浮點數(64位)。浮點數的基本格式如下:
各部分含義如下:
sign:符號位,0表示正,1表示負
exponent:階碼,浮點數的冪次。一般採用移碼錶示。
fraction:浮點數的小數部分 (理解:不管十進位制的整數or小數,都要表示成2進位制,是1.開頭的小數,通過指數的大小,控制小數點的位移)
上述格式描述的浮點數的十進位制值為V=(-1)^SX(1.fraction)X2^E。其中(-1)^S表示符號,1.fraction是二進位制的小數,2^E表示冪次,類似於二進位制的科學計數法。由於除0外的所有小數都可以寫成1.fractionX2^E的形式,因而,在表示浮點數時,省略掉了前面的整數部分1.
對於單精度浮點數,S是1位,E是8位,小數部分是23位。對於雙精度浮點數,S是1位,E是11位,小數部分是52位。指數部分E有正負性,使用移碼錶示。8位E要表示正負,一般減去127,23位則是減去1023。例如,實際的小數指數部分是0的話,在單精度浮點數表示中,E部分是127.
上面描述的是規格化的浮點數,如果浮點數的階碼部分全0或者全1,則表示非規格化的浮點數。
(1)階碼不是全0或全1,規格化浮點數。
(2)階碼全0:表示0.fractionX2^-126次。注意,此時指數部分是1-127.這一類表示了接近0的小數部分。
(3)階碼全1:如果小數部分全0,表示正負無窮大。如果出現1,表示不是一個數(NaN)。
浮點數精度
通過上面的介紹可以發現,浮點數的精度取決於二進位制小數部分的精度。對於單精度浮點數,小數部分有23位,對應十進位制小數見下表:
| 二進位制小數 | 十進位制小數 |
| 2^-23 | 0.00000011920928955078125 |
| 2^-22 | 0.0000002384185791015625 |
| 2^-21 | 0.000000476837158203125 |
| 2^-20 | 0.00000095367431640625 |
| 2^-19 | 0.0000019073486328125 |
| 2^-18 | 0.000003814697265625 |
由於是規格化的浮點數,所以小數部分都要加上1,可以知道,單精度浮點數的小數部分最小是1.00000011920928955078125,其次是1.0000002384185791015625,注意到這兩個小數之間是有間隔的,如果要表示1.0000001和1.0000002之間的小數,則單精度浮點數無能為力,1.0000001已經是23位小數部分描述的最小值了。通過這樣的分析可以發現,23位只能描述到小數點後第7位,即1.0000001,1.0000002,1.0000004,1.0000009對應了二進位制的小數值,其他要通過上面幾個的組合來表示。
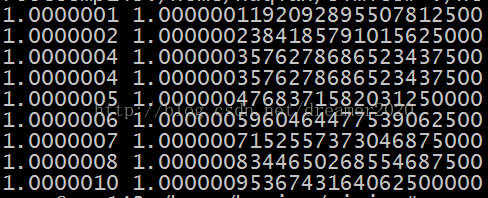
事實上,如果考慮第八位的舍入,1.0000004,1.0000009本身的表示也是不準確的。為了驗證這一點,通過程式將1.0000001到1.0000009的結果均打印出來,得如下:
程式中直接將1.0000001到1.0000009分別賦給float型變數,左邊一列是輸出時小數點後保留7位的結果,右邊是保留了25位的結果。
通過上面的結果可以發現,小數點後第7位是部分準確的。例如,1.0000004就是1.00000035通過得到的,其實際儲存和1.0000003相同。1.0000006也是通過舍入得到的。再往前第6位及以後均可以通過小數準確表示出來。通常說float資料的有效位是6~7位,也是這個原因。
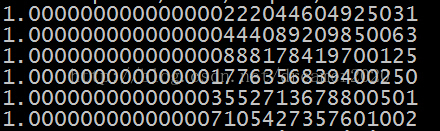
類似的分析,雙精度浮點數小數部分有52位,和上面類似,最低6位(2^-52,2^-51,......)表示的規格化小數如下所示。從圖中可以看出,雙精度浮點數能準確表示到小數點後第15位,第16位部分準確。
整數轉化為浮點數
那麼如果一個整數用float來儲存,儲存的精度有多少呢?首先,我們需要將整數轉化為二進位制科學計數法形式,然後再對應到規格化浮點數中。在處理小數部分時,多餘的數位即為損失的精度。
可以測試二進位制整數1000 0000 0000 0000 0000 0001,即小數點後面剛好23位。下圖展示了小數點後23位、24位及0位的輸出結果。只有小數點後24位這一種情況資料表示是不準確的,雖然損失的小數點後第24位,但在科學計數法的前提下,真實值相差為1.
由此可以確定,從1到0xFFFFFF(24位全1,16777215)的整數均可以表示為不超過24位的二進位制整數,小數部分不超過23位,因而可以準確的用浮點數表示。還有一部分整數,在表示為二進位制的科學計數法時,小數部分不超過23位,也可以準確表示,除此外,其他整數,轉化為float後均會損失精度。
一般來說,無論是整數或者小數,用float表示時,從左邊第一個非0的數字算起,從高到低的7位是準確的。此後的數位是不能保證精確的。
相應的,從1到0x1FFFFFFFFFFFFF(53位全1,18014398509481983)均可以準確用double來表示。其他整數,只有在轉化為double時小數部分不超過52位才可以精確表示。否則,會有一定的精度損失。無論整數或者小數,用double表示時,從左邊第一個非0的數字起,從高到低的16位是準確的,此後的數位不一定精確。
浮點數分佈
通過上面的分析可以發現,儘管浮點數表示的範圍很廣,但由於精度損失的存在,加上冪次的放大作用,一個浮點數實際上是表示了周圍的一個有理數區間。如果將浮點數繪製到一個數軸上,直觀上看,靠近0的部分,浮點數出現較密集。越靠近無窮大,浮點數分佈越稀疏,一個浮點值代表了周圍一片資料。如下圖所示。從這個意義上來說,浮點數不宜直接比較相等,它們是代表了一個數據範圍。實際應用中,如果要使用浮點數計算,一定要考慮精度問題。在滿足精度要求的前提下,計算結果才是有效的。
在計算精度要求情形下,例如商業計算等,應該避免使用浮點數,嚴格採取高精度計算。
本文分析到此結束。主要想告訴讀者浮點數在什麼時候使用是可靠的,在什麼時候使用會出現精度問題。歡迎大家討論。