機器學習之--最大似然估計
1.最大似然估計概念:
最大似然估計,只是一種概率論在統計學的應用,它是引數估計的方法之一。說的是已知某個隨機樣本滿足某種概率分佈,但是其中具體的引數不清楚,引數估計就是通過若干次試驗,觀察其結果,利用結果推出引數的大概值。最大似然估計是建立在這樣的思想上:已知某個引數能使這個樣本出現的概率最大,我們當然不會再去選擇其他小概率的樣本,所以乾脆就把這個引數作為估計的真實值。
4. 關於概率密度(PDF)
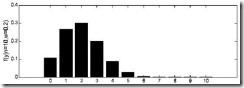
我們來考慮個簡單的情況(m=k=1),即是引數和樣本都為1的情況。假設進行一個實驗,實驗次數定為10次,每次實驗成功率為0.2,那麼不成功的概率為0.8,用y來表示成功的次數。由於前後的實驗是相互獨立的,所以可以計算得到成功的次數的概率密度為:
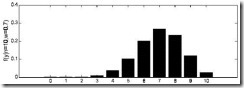
由於y的取值範圍已定,而且![]() 也為已知,所以圖1顯示了y取不同值時的概率分佈情況,而圖2顯示了當
也為已知,所以圖1顯示了y取不同值時的概率分佈情況,而圖2顯示了當![]() 時的y值概率情況。
時的y值概率情況。
那麼![]() 在[0,1]之間變化而形成的概率密度函式的集合就形成了一個模型。
在[0,1]之間變化而形成的概率密度函式的集合就形成了一個模型。
5. 最大似然估計的求法
由上面的介紹可以知道,對於圖1這種情況y=2是最有可能發生的事件。但是在現實中我們還會面臨另外一種情況:我們已經知道了一系列的觀察值和一個感興趣的模型,現在需要找出是哪個PDF(具體來說引數![]() 為多少時)產生出來的這些觀察值。要解決這個問題,就需要用到引數估計的方法,在最大似然估計法中,我們對調PDF中資料向量和引數向量的角色,於是可以得到似然函式的定義為:
為多少時)產生出來的這些觀察值。要解決這個問題,就需要用到引數估計的方法,在最大似然估計法中,我們對調PDF中資料向量和引數向量的角色,於是可以得到似然函式的定義為:
該函式可以理解為,在給定了樣本值的情況下,關於引數向量![]() 取值情況的函式。還是以上面的簡單實驗情況為例,若此時給定y為7,那麼可以得到關於
取值情況的函式。還是以上面的簡單實驗情況為例,若此時給定y為7,那麼可以得到關於![]() 的似然函式為:
的似然函式為:
繼續回顧前面所講,圖1,2是在給定![]() 的情況下,樣本向量y取值概率的分佈情況;而圖3是圖1,2橫縱座標軸相交換而成,它所描述的似然函式圖則指出在給定樣本向量y的情況下,符合該取值樣本分佈的各種引數向量
的情況下,樣本向量y取值概率的分佈情況;而圖3是圖1,2橫縱座標軸相交換而成,它所描述的似然函式圖則指出在給定樣本向量y的情況下,符合該取值樣本分佈的各種引數向量![]() 的可能性。若
的可能性。若![]() 相比於
相比於![]() ,使得y=7出現的可能性要高,那麼理所當然的
,使得y=7出現的可能性要高,那麼理所當然的![]() 要比
要比![]() 更加接近於真正的估計引數。所以求
更加接近於真正的估計引數。所以求![]() 的極大似然估計就歸結為求似然函式
的極大似然估計就歸結為求似然函式![]() 的最大值點。那麼
的最大值點。那麼![]() 取何值時似然函式
取何值時似然函式![]() 最大,這就需要用到高等數學中求導的概念,如果是多維引數向量那麼就是求偏導。
最大,這就需要用到高等數學中求導的概念,如果是多維引數向量那麼就是求偏導。
主要注意的是多數情況下,直接對變數進行求導反而會使得計算式子更加的複雜,此時可以借用對數函式。由於對數函式是單調增函式,所以![]() 與
與![]() 具有相同的最大值點,而在許多情況下,求
具有相同的最大值點,而在許多情況下,求![]() 的最大值點比較簡單。於是,我們將求
的最大值點比較簡單。於是,我們將求![]() 的最大值點改為求
的最大值點改為求![]() 的最大值點。
的最大值點。
若該似然函式的導數存在,那麼對![]() 關於引數向量的各個引數求導數(當前情況向量維數為1),並命其等於零,得到方程組:
關於引數向量的各個引數求導數(當前情況向量維數為1),並命其等於零,得到方程組:
可以求得![]() 時似然函式有極值,為了進一步判斷該點位最大值而不是最小值,可以繼續求二階導來判斷函式的凹凸性,如果
時似然函式有極值,為了進一步判斷該點位最大值而不是最小值,可以繼續求二階導來判斷函式的凹凸性,如果![]() 的二階導為負數那麼即是最大值,這裡再不細說。
的二階導為負數那麼即是最大值,這裡再不細說。
還要指出,若函式![]() 關於
關於![]() 的導數不存在,我們就無法得到似然方程組,這時就必須用其它的方法來求最大似然估計值,例如用有界函式的增減性去求
的導數不存在,我們就無法得到似然方程組,這時就必須用其它的方法來求最大似然估計值,例如用有界函式的增減性去求![]() 的最大值點
的最大值點
6. 總結
最大似然估計,只是一種概率論在統計學的應用,它是引數估計的方法之一。說的是已知某個隨機樣本滿足某種概率分佈,但是其中具體的引數不清楚,引數估計就是通過若干次試驗,觀察其結果,利用結果推出引數的大概值。最大似然估計是建立在這樣的思想上:已知某個引數能使這個樣本出現的概率最大,我們當然不會再去選擇其他小概率的樣本,所以乾脆就把這個引數作為估計的真實值。
求最大似然函式估計值的一般步驟:
(1) 寫出似然函式
(2) 對似然函式取對數,並整理
(3) 求導數
(4) 解似然方程
對於最大似然估計方法的應用,需要結合特定的環境,因為它需要你提供樣本的已知模型進而來估算引數,例如在模式識別中,我們可以規定目標符合高斯模型。而且對於該演算法,我理解為,“知道”和“能用”就行,沒必要在程式設計時將該部分實現,因為在大多數程式中只會用到我最後推匯出來的結果。個人建議,如有問題望有經驗者指出。在文獻[1]中講解了本文的相關理論內容,在文獻[2]附有3個推導例子。