拓撲排序(佇列實現)
阿新 • • 發佈:2018-11-29
什麼是拓撲排序呢?就是將一個有向無環圖中所有頂點在不違反先決條件關係的前提下排成線性序列的過程稱為拓撲排序。
學拓撲排序有什麼用呢?當然有用啦~。比如說學校排課的時候,會考慮到有的課程需要先修。我們學完C程式設計這門課,有了程式設計基礎,然後才能學習資料結構。大學要修很多門課程的,人為的去排課很頭痛的,這時候就可以用拓撲排序解決這個問題。
拓撲排序只針對有向無環圖(DAG),有兩種方法可以實現,一種是佇列實現,另外一種是深搜(DFS)實現。
這裡先介紹佇列實現的方法。
(1)從圖中選擇任意一個入度為0的頂點且輸出
(2)從圖中刪掉此頂點及所有的出邊,將其入度減少1
(3)回到第(1)步繼續執行
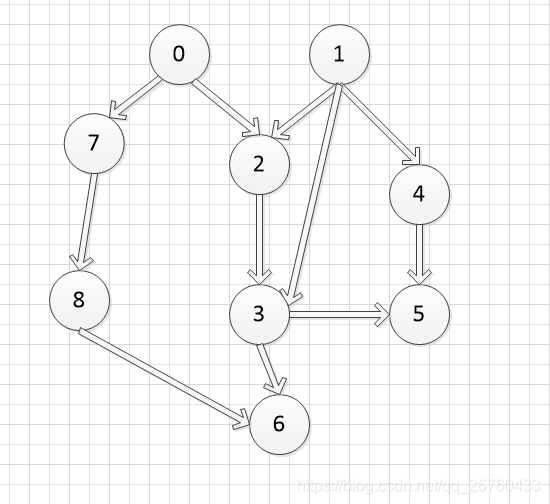
我們對上面圖進行拓撲排序,我這裡採用的是鄰接表儲存圖,貼程式碼。
#include<vector>
#include<iostream>
#include<queue>
using namespace std;
class Graph
{
int v; //頂點個數
vector<int> *adj; //鄰接表
int *indegree; //每個頂點的入度
public:
Graph(int n); //建構函式 執行結果

圖的每條邊處理一次,圖的每個頂點訪問一次,採用鄰接表表示時時間複雜度為 O(n+e)。採用相鄰矩陣表示時,為O(n*n)。
對DFS實現拓撲排序有興趣的,點選:拓撲排序DFS版
PS:本人小白,第一次寫部落格,有點緊張,嘻嘻~。
