拓撲排序是針對有向無圈圖的頂點的一種排序，使得如果存在一條從A到B的路徑，那麼在排序中A必定在B的前面。

拓撲排序的應用場景很好理解，比如在記憶體中執行著很多工，某個任務A的執行依賴於另外一個任務B，那麼在A執行完之前，B一定不能被清理。而另外一些任務是沒有關聯的，如何來安排這些任務被清理的順序就需要依賴拓撲排序。

一個簡單的拓撲排序的方案(Kahn演算法)是：先找出任意一個沒有入邊的頂點，然後列印該頂點，並將它及其邊一起從圖中剔除，然後對其餘的部分繼續這個操作。

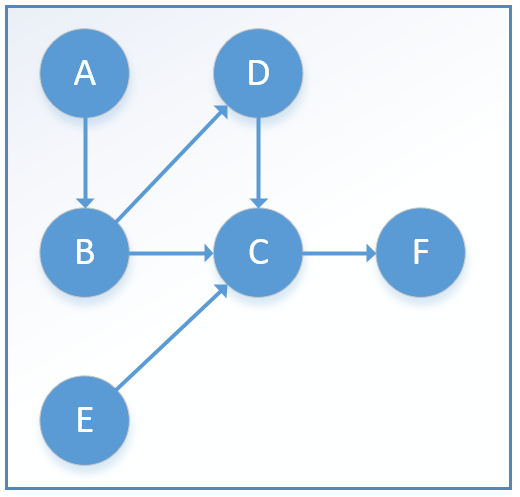
這個思路很簡單，下面來做具體的實現。針對一個圖，如下，來做拓撲排序，使用Java來實現。

需要新建三個類：節點、圖、Kahn演算法

具體的程式碼和註釋如下：

package com.algorithm;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Queue;
import java.util.Set;

/**
 * 拓撲排序，當前方案並沒有在節點類中加入過多的內容
 * 但是在圖類中加入了邊的集合adjaNode
 */
public class TopoSortB {

	/**
	 * 拓撲排序節點類
	 */
	private static class Node {
		public Object val;
		public int pathIn = 0; // 入鏈路數量
		public Node(Object val) {
			this.val = val;
		}
	}

	/**
	 * 拓撲圖類
	 */
	private static class Graph {
		// 圖中節點的集合
		public Set<Node> vertexSet = new HashSet<Node>();
		// 相鄰的節點，紀錄邊
		public Map<Node, Set<Node>> adjaNode = new HashMap<Node, Set<Node>>();

		// 將節點加入圖中
		public boolean addNode(Node start, Node end) {
			if (!vertexSet.contains(start)) {
				vertexSet.add(start);
			}
			if (!vertexSet.contains(end)) {
				vertexSet.add(end);
			}
			if (adjaNode.containsKey(start)
					&& adjaNode.get(start).contains(end)) {
				return false;
			}
			if (adjaNode.containsKey(start)) {
				adjaNode.get(start).add(end);
			} else {
				Set<Node> temp = new HashSet<Node>();
				temp.add(end);
				adjaNode.put(start, temp);
			}
			end.pathIn++;
			return true;
		}
	}

	//Kahn演算法
	private static class KahnTopo {
		private List<Node> result; // 用來儲存結果集
		private Queue<Node> setOfZeroIndegree; // 用來儲存入度為0的頂點
		private Graph graph;

		//建構函式，初始化
		public KahnTopo(Graph di) {
			this.graph = di;
			this.result = new ArrayList<Node>();
			this.setOfZeroIndegree = new LinkedList<Node>();
			// 對入度為0的集合進行初始化
			for(Node iterator : this.graph.vertexSet){
				if(iterator.pathIn == 0){
					this.setOfZeroIndegree.add(iterator);
				}
			}
		}

		//拓撲排序處理過程
		private void process() {
			while (!setOfZeroIndegree.isEmpty()) {
				Node v = setOfZeroIndegree.poll();
				
				// 將當前頂點新增到結果集中
				result.add(v);
				
				if(this.graph.adjaNode.keySet().isEmpty()){
					return;
				}
				
				// 遍歷由v引出的所有邊
				for (Node w : this.graph.adjaNode.get(v) ) {
					// 將該邊從圖中移除，通過減少邊的數量來表示
					w.pathIn--;
					if (0 == w.pathIn) // 如果入度為0，那麼加入入度為0的集合
					{
						setOfZeroIndegree.add(w);
					}
				}
				this.graph.vertexSet.remove(v);
				this.graph.adjaNode.remove(v);
			}
			
			// 如果此時圖中還存在邊，那麼說明圖中含有環路
			if (!this.graph.vertexSet.isEmpty()) {
				throw new IllegalArgumentException("Has Cycle !");
			}
		}

		//結果集
		public Iterable<Node> getResult() {
			return result;
		}
	}
	
	//測試
	public static void main(String[] args) {
		Node A = new Node("A");
		Node B = new Node("B");
		Node C = new Node("C");
		Node D = new Node("D");
		Node E = new Node("E");
		Node F = new Node("F");
		
		Graph graph = new Graph();
		graph.addNode(A, B);
		graph.addNode(B, C);
		graph.addNode(B, D);
		graph.addNode(D, C);
		graph.addNode(E, C);
		graph.addNode(C, F);
		
		KahnTopo topo = new KahnTopo(graph);
		topo.process();
		for(Node temp : topo.getResult()){
			System.out.print(temp.val.toString() + "-->");
		}
	}
	
}