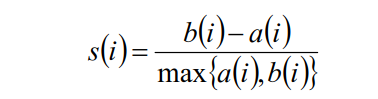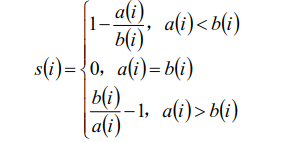K-means演算法延伸
對於之前的一篇文章中說過K-means雖然效果可以，但是對給定的K值敏感，簇中心位置敏感以及計算量大。所以針對以上兩點有了一些優化的方法。
對於給定的K值偏大或者偏小都將影響聚類效果。而由於對於需要聚類的資料本身沒有一個y值即分類值，這正是需要演算法最後得出的。所以一般對於不給定K值的話，可以通過canopy 演算法來確定K值。
Canopy演算法
Canopy演算法屬於一種“粗”聚類演算法，執行速度較快，但精度較低，演算法
執行步驟如下：
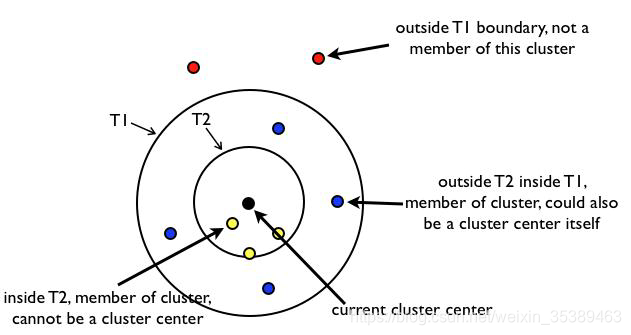
• 給定樣本列表L=x1,x,2…,xm以及先驗值r1和r2(r1>r2)
• 從列表L中獲取一個節點P，計算P到所有聚簇中心點的距離(如果不存在聚簇中心，
那麼此時點P形成一個新的聚簇)，並選擇出最小距離D(P,aj)
• 如果距離D小於r1，表示該節點屬於該聚簇，新增到該聚簇列表中
• 如果距離D小於r2，表示該節點不僅僅屬於該聚簇，還表示和當前聚簇中心點非常近，
所以將該聚簇的中心點設定為該簇中所有樣本的中心點，並將P從列表L中刪除
• 如果距離D大於r1，那麼節點P形成一個新的聚簇，並將P從列表L中刪除
• 直到列表L中的元素資料不再有變化或者元素數量為0的時候，結束迴圈操作
Canopy演算法得到的最終結果的值，聚簇之間是可能存在重疊的，但是不會
存在某個物件不屬於任何聚簇的情

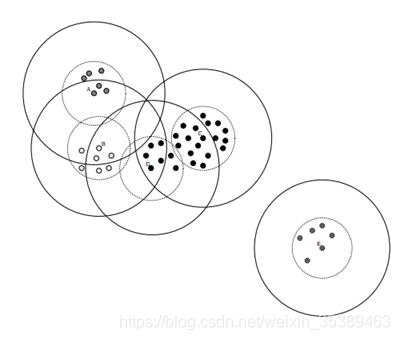
Canopy演算法常用應用場景
由於K-Means演算法存在初始聚簇中心點敏感的問題，常用使用Canopy+K-
Means演算法混合形式進行模型構建
• 先使用canopy演算法進行“粗”聚類得到K個聚類中心點
• K-Means演算法使用Canopy演算法得到的K個聚類中心點作為初始中心點，進行“細”
聚類
• 優點：
• 執行速度快(先進行了一次聚簇中心點選擇的預處理)
• 不需要給定K值，應用場景多
• 能夠緩解K-Means演算法對於初始聚類中心點敏感的問題
K值的問題解決了，該解決簇中心的問題了。對於簇中心的解決演算法有K-Means++演算法和K-Means||演算法，後者是前者的更進一步改進。
K-Means++演算法
•解決K-Means演算法對初始簇心比較敏感的問題，K-Means++演算法和K-
Means演算法的區別主要在於初始的K箇中心點的選擇方面，K-Means演算法使
用隨機給定的方式，K-Means++演算法採用下列步驟給定K個初始質點：
• 從資料集中任選一個節點作為第一個聚類中心
• 對資料集中的每個點x，計算x到所有已有聚類中心點的距離和D(X)，基於D(X)採用
線性概率選擇出下一個聚類中心點(距離較遠的一個點成為新增的一個聚類中心點)
• 重複步驟2直到找到k個聚類中心點
• 缺點：由於聚類中心點選擇過程中的內在有序性，在擴充套件方面存在著效能方
面的問題(第k個聚類中心點的選擇依賴前k-1個聚類中心點的值)
K-Means||演算法
解決K-Means++演算法缺點而產生的一種演算法；主要思路是改變每次遍歷時
候的取樣規則，並非按照K-Means++演算法每次遍歷只獲取一個樣本，而是
每次獲取K個樣本，重複該取樣操作O(logn)次，然後再將這些抽樣出來的
樣本聚類出K個點，最後使用這K個點作為K-Means演算法的初始聚簇中心點。
實踐證明：一般5次重複採用就可以保證一個比較好的聚簇中心點。
看似K-means的問題幾乎解決了，但是有一點不容忽視，就是計算量大。對於計算量的話，可以參照以前的梯度下降法中的小批量梯度下降法。這裡也可以進行小批量的K-means演算法叫做Mini Batch K-Means演算法
Mini Batch K-Means演算法
• Mini Batch K-Means演算法是K-Means演算法的一種優化變種，採用小規模的資料子集(每次
訓練使用的資料集是在訓練演算法的時候隨機抽取的資料子集)減少計算時間，同時試圖優化
目標函式；Mini Batch K-Means演算法可以減少K-Means演算法的收斂時間，而且產生的結
果效果只是略差於標準K-Means演算法
• 演算法步驟如下：
• 首先抽取部分資料集，使用K-Means演算法構建出K個聚簇點的模型
• 繼續抽取訓練資料集中的部分資料集樣本資料，並將其新增到模型中，分配給距離最近的聚簇中心點
• 更新聚簇的中心點值(每次更新都只用抽取出來的部分資料集)
• 迴圈迭代第二步和第三步操作，直到中心點穩定或者達到迭代次數，停止計算操作
一般的話Mini Batch K-Means是 K-means演算法的3倍執行速度。
說了這麼多，到目前位置還沒有提到衡量聚類演算法好壞的指標。像監督學習還要損失函式，而聚類的話則沒有損失函式之說，但是聚類演算法也有幾個衡量指標，比如：
• 混淆矩陣
• 均一性
• 完整性
• V-measure
• 調整蘭德係數(ARI)
• 調整互資訊(AMI)
• 輪廓係數(Silhouette)
但是常用的指標是輪廓係數。
聚類演算法的衡量指標-輪廓係數
• 簇內不相似度：計算樣本i到同簇其它樣本的平均距離為ai;ai越小，表示樣本i越
應該被聚類到該簇，簇C中的所有樣本的ai的均值被稱為簇C的簇不相似度。
• 簇間不相似度：計算樣本i到其它簇Cj的所有樣本的平均距離bij，
bi=min{bi1,bi2,…,bik}；bi越大，表示樣本i越不屬於其它簇。
• 輪廓係數：si值越接近1表示樣本i聚類越合理，越接近-1，表示樣本i應該分類
到另外的簇中，近似為0，表示樣本i應該在邊界上；所有樣本的si的均值被成為
聚類結果的輪廓係數