一、導數

• 導數 就是曲線的斜率，是曲線變化快慢的一個反應。
• 二階導數 是斜率變化的反應，表現曲線的 凹凸性

$y=f\left(x\right)$

y = f(x)
$y^{\mathrm{\prime }}=f^{\mathrm{\prime }}($

x ) = d y d x

= lim ⁡ Δ x → 0 Δ y Δ x = lim ⁡ Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x y' = f'(x) = \frac{dy}{dx}=\lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x \rightarrow 0}\frac{f(x_0+\Delta x) - f(x_0)}{\Delta x}

關於導數相關的知識，可參考高等數學

二、偏導數

導數是針對單一變數的，當函式是多變數的，偏導數 就是關於其中一個變數的導數而保持其他變數恆定不變（固定一個變數求導數）。

假定一個二元函式 $z = f(x,y)$，點 $(x_0, y_0)$ 是其定義域內的一個點，將 $y$ 固定在 $y_0$ 上，而 $x$ 在 $x_0$ 上增量 $\Delta x$，相應的函式 $z$ 有增量 $\Delta z = f(x_0+\Delta x, y_0) - f(x_0, y_0)$； $\Delta z$和 $\Delta x$的比值當 $\Delta x$ 的值趨向於0的時候，如果極限存在，那麼此極限稱為函式 $z = f(x,y)$ 在點 $(x_0, y_0)$ 處對 $x$的偏導數，記作： $f'_x(x_0,y_0)$

對 $x$ 的偏導數：
$\frac{\partial f}{\partial x} \big| (x=x_0,y=y_0)$
對 $y$ 的偏導數：
$\frac{\partial f}{\partial y} \big| (x=x_0,y=y_0)$

三、梯度

梯度是一個向量，表示某一函式在該點處的 方向導數 ，沿著該方向取最大值，即函式在該點處沿著該方向變化最快，變化率最大（即該梯度向量的模）；當函式為一維函式的時候，梯度就是導數。

$\Delta f(x_1,x_2) = \bigg(\frac{\partial f(x_1,x_2)}{\partial x_1},\frac{\partial f(x_1,x_2)}{\partial x_2}\bigg)$

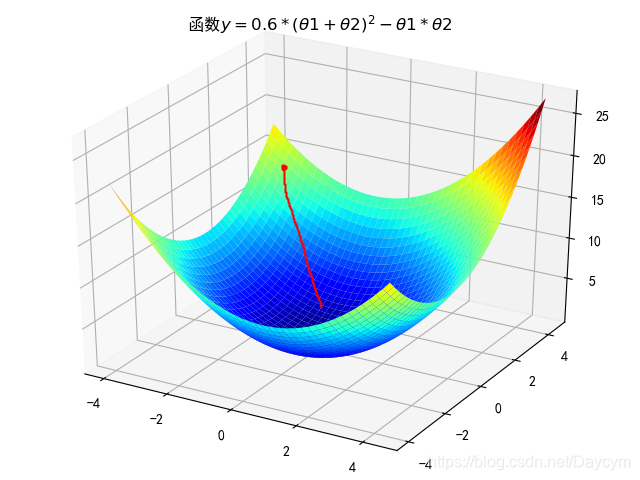
四、梯度下降法

梯度下降法 常用於求解無約束情況下凸函式的極小值，是一種迭代型別的演算法，因為凸函式只有一個極值點，故求解出來的極小值就是函式的最小值點。

$J(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_{\theta}(x^{(i)}) - y^{(i)} ) ^2$

相關推薦