有一個n*m的表格，格子(i,j)中的數w是σ(gcd(i,j))。

Q組詢問，每次給出n,m,a。求表中所有不超過a的w之和。

題解：

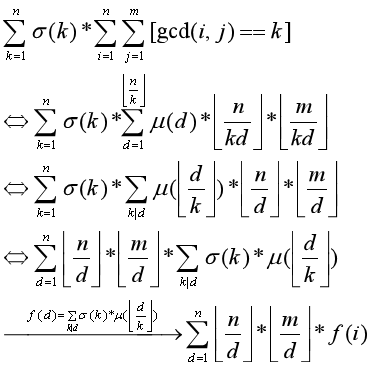
然後後面的用樹狀陣列動態更新即可。

程式碼：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 100050
#define ll long long
#define MOD 2147483647
int pri[N],cnt,mu[N],d[N];
ll sig[N];
bool vis[N];
 
int K[N];
bool cmpk(int a,int b)
{
    return sig[a]<sig[b];
}
void get_mu()
{
    mu[1]=1;
    sig[1]=1;
    for(int i=2;i<=100000;i++)
    {
        if(!vis[i])
        {
            pri[++cnt]=i;
            d[i]=1+i;
            sig[i]=1+i;
            mu[i]=-1;
        }
        for(int j=1;j<=cnt&&i*pri[j]<=100000
 
;j++)
        {
            vis[i*pri[j]]=1;
            if(i%pri[j])
            {
                mu[i*pri[j]]=-mu[i];
                d[i*pri[j]]=d[pri[j]];
                sig[i*pri[j]]=sig[pri[j]]*sig[i];
            }else
            {
                sig[i*pri[j]]=sig[i]/d[i];
                d[i
 
*pri[j]]=d[i]*pri[j]+1;
                sig[i*pri[j]]*=d[i*pri[j]];
                break;
            }
        }
    }
}
struct Ques
{
    int n,m,a,id;
}q[20050];
int ans[20050];
bool cmp(Ques x,Ques y)
{
    return x.a<y.a;
}
int f[N];
void up(int x,int d)
{
    if(!x)return ;
    while(x<=100000)
    {
        f[x]+=d;
        x+=(x&(-x));
    }
}
int down(int x)
{
    if(!x)return 0;
    int ret = 0;
    while(x)
    {
        ret+=f[x];
        x-=(x&(-x));
    }
    return ret;
}
int Q;
int main()
{
    scanf("%d",&Q);
    get_mu();
    for(int i=1;i<=100000;i++)K[i]=i;
    sort(K+1,K+100001,cmpk);
    for(int i=1;i<=Q;i++)
    {
        scanf("%d%d%d",&q[i].n,&q[i].m,&q[i].a);
        if(q[i].n>q[i].m)swap(q[i].n,q[i].m);
        q[i].id=i;
    }
    sort(q+1,q+1+Q,cmp);
    for(int i=1,tl=1;i<=Q;i++)
    {
        while(sig[K[tl]]<=q[i].a&&tl<=100000)
        {
            for(int j=1;K[tl]*j<=100000;j++)
            {
                up(K[tl]*j,mu[j]*sig[K[tl]]);
            }
            tl++;
        }
        int ret = 0;
        for(int j=1,nxt;j<=q[i].n;j=nxt+1)
        {
            nxt = min(q[i].n/(q[i].n/j),q[i].m/(q[i].m/j));
            ret+=(down(nxt)-down(j-1))*(q[i].n/j)*(q[i].m/j);
        }
        ret&=MOD;
        ans[q[i].id]=ret;
    }
    for(int i=1;i<=Q;i++)
        printf("%d\n",ans[i]);
    return 0;
}