CNN 反捲積原理解析
阿新 • • 發佈:2018-12-01

反捲積(Deconvolution)的概念第一次出現是Zeiler在2010年發表的論文 Deconvolutional networks 中,但是並沒有指定反捲積這個名字,反捲積這個術語正式的使用是在其之後的工作中( Adaptive deconvolutional networks for mid and high level feature learning )。隨著反捲積在神經網路視覺化上的成功應用,其被越來越多的工作所採納比如:場景分割、生成模型等。其中反捲積(Deconvolution)也有很多其他的叫法,比如:Transposed Convolution,Fractional Strided Convolution等等。
這篇文章的目的主要有兩方面:
1. 解釋卷積層和反捲積層之間的關係;
2. 弄清楚反捲積層輸入特徵大小和輸出特徵大小之間的關係。
## 卷積層
卷積層大家應該都很熟悉了,為了方便說明,定義如下:






我們再把4×4的輸入特徵展成[16,1]的矩陣X ,那麼Y = CX則是一個[4,1]的輸出特徵矩陣,把它重新排列2×2的輸出特徵就得到最終的結果,從上述分析可以看出卷積層的計算其實是可以轉化成矩陣相乘的。值得注意的是,在一些深度學習網路的開源框架中並不是通過這種這個轉換方法來計算卷積的,因為這個轉換會存在很多無用的0乘操作,Caffe中具體實現卷積計算的方法可參考Implementing convolution as a matrix multiplication。
反捲積和卷積的關係

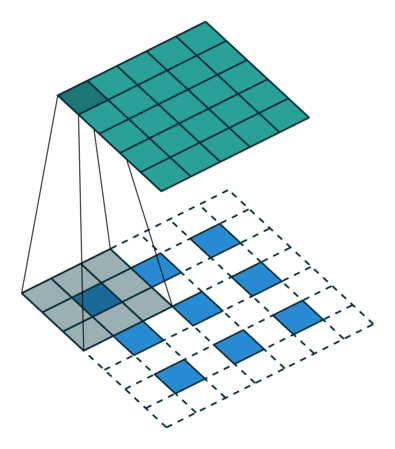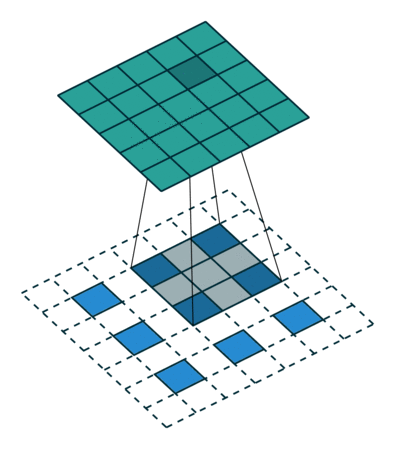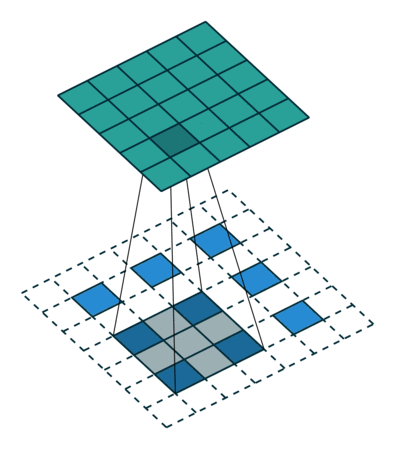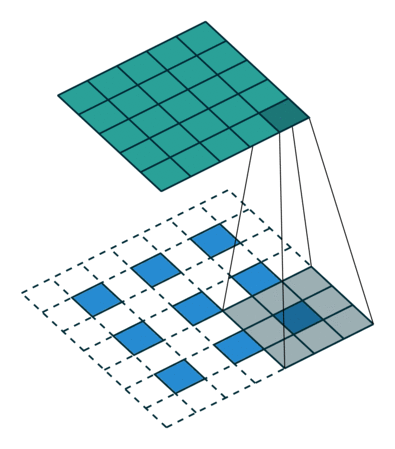
參考
Is the deconvolution layer the same as a convolutional layer?

反捲積(Deconvolution)的概念第一次出現是Zeiler在2010年發表的論文 Deconvolutional networks 中,但是並沒有指定反捲積這個名字,反捲積這個術語正式的使用是在其之後的工作中( Adaptive deconvolutional networks for mid and high level feature learning )。隨著反捲積在神經網路視覺化上的成功應用,其被越來越多的工作所採納比如:場景分割、生成模型等。其中反捲積(Deconvolution)也有很多其他的叫法,比如:Transposed Convolution,Fractional Strided Convolution等等。
這篇文章的目的主要有兩方面:
1. 解釋卷積層和反捲積層之間的關係;
2. 弄清楚反捲積層輸入特徵大小和輸出特徵大小之間的關係。
## 卷積層
卷積層大家應該都很熟悉了,為了方便說明,定義如下:






我們再把4×4的輸入特徵展成[16,1]的矩陣X ,那麼Y = CX則是一個[4,1]的輸出特徵矩陣,把它重新排列2×2的輸出特徵就得到最終的結果,從上述分析可以看出卷積層的計算其實是可以轉化成矩陣相乘的。值得注意的是,在一些深度學習網路的開源框架中並不是通過這種這個轉換方法來計算卷積的,因為這個轉換會存在很多無用的0乘操作,Caffe中具體實現卷積計算的方法可參考Implementing convolution as a matrix multiplication。
通過上述的分析,我們已經知道卷積層的前向操作可以表示為和矩陣 C 相乘,那麼 我們很容易得到卷積層的反向傳播就是和 C 的轉置相乘 。反捲積和卷積的關係


參考
Is the deconvolution layer the same as a convolutional layer?
轉載過程中有些元素可能有缺失 具體請參考原文:https://buptldy. github.io/2016/10/29/2016-10-29-deconv/

