離散優化模型的進階-什麼是效率低的模型如何改進他們 week1-2
離散優化模型的進階 week1-2
對基本模型的提升
問題描述
一個優化問題描述如下,張飛要通過使用稻草人佈置疑陣的方式來虛張聲勢有這樣的約束:
- 疑陣有n行和n列
- 所有的稻草人高度相同
- 所有的稻草人必須臨近一個真實的士兵
- 所有的稻草人前邊一定要有一個比他高的真實的士兵
- 目標是將疑陣填充的最大
資料定義:

nsoldier 是真實士兵的人數
soldier代表一個士兵
soldier0代表這個位置是一個士兵或者是一個稻草人。
strawheight 是稻草人的身高
height 是所有的真實士兵的身高
還定義了最大的行數和最大的列數
決策變數

其中定義了士兵和稻草人的位置,
還有排列的行數和列數。
約束條件:

約束描述了一個士兵出現最多一次,具體來說對任意不同行且不同列的兩個位置,要麼其中一個是稻草人,要麼兩個士兵不是同一個人。
這是一個非常直觀的描述,但是同時這個描述非常的沒有效率。
因為我們要在我們的約束表中加入x[r1,r2]=0這個約束非常多次。以及對任何的約束,迴圈都會讓他們加入兩次。
對於一個高效的模型,一般有一下的幾個特點:
- 確保不加入一個約束多次
- 確保不在迴圈中重複約束
- 確保儘早的在迴圈中加入約束
然後修改上述的模型描述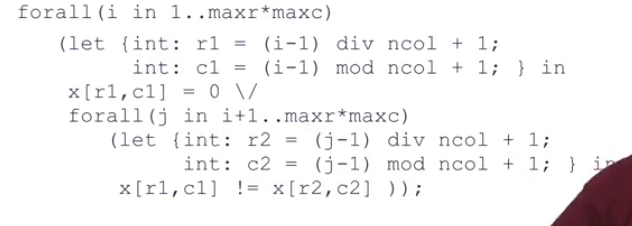
這樣的修改使用了let語句定義了臨時的變數,將多餘的約束刪除掉了。
不過我們還有更好的方法。
如果你熟悉minizinc的全域性約束
可以使用
下面需要約束的是士兵出現最少一次
這樣的模型同樣是非常的沒有效率的,這種模型的約束非常的分離。
我們使用下面的方法來修正這種模型。
下面的約束是,每一個稻草人周圍都有一個真實的士兵。
這種描述使用if語句進行,但是通常優秀的模型都沒有使用if語句
然後是關於身高的約束:
不過這種模型同樣效率不高,我們使用一個新的變數變數來更好的描述這個問題。
在建模中應該儘量避免如下的幾個問題的使用:
- not函式,如果想要使用 not a=b 請修改成 a != b
- 析取模型,如果 如 a/b如果必須使用,請確保這個模型儘量簡單。
- 推斷, 如果必須使用,請確保這個模型儘量簡單。
- 不要在迴圈中使用 exist
上面的做法都會讓模型變得十分的複雜。
最後建立的模型就是這個樣子的:
% Parading the soldiers
int: nsoldier;
set of int: SOLDIER = 1..nsoldier;
set of int: SOLDIER0 = 0..nsoldier;
array[SOLDIER] of int: height;
int: strawheight;
int: maxr;
set of int: ROW = 1..maxr;
int: maxc;
set of int: COL = 1..maxc;
var ROW: nrow; % size of rectangle of soldiers
var COL: ncol;
array[ROW,COL] of var SOLDIER0: x;
% all real soldiers appear in the first nrow rows and ncol cols
%constraint forall(r in nrow+1..maxr, c in ncol+1..maxc)
% (x[r,c] = 0);
constraint forall(r in ROW, c in COL)
( (r > nrow -> x[r,c] = 0)
/\ (c > ncol -> x[r,c] = 0));
% soldiers are different positions
%constraint forall(r1, r2 in ROW, c1, c2 in COL where r1 != r2 \/ c1 != c2)
% (x[r1,c1] = 0 \/ x[r1,c1] != x[r2,c2]);
%constraint forall(i in 1..maxr*maxc)
% (let {int: r1 = (i-1) div maxc + 1;
% int: c1 = (i-1) mod maxc + 1; } in
% x[r1,c1] = 0 \/
% forall(j in i+1..maxr*maxc)
% (let {int: r2 = (j-1) div maxc + 1;
% int: c2 = (j-1) mod maxc + 1; } in
% trace("x[\(r1),\(c1)] != x[\(r2),\(c2)]\n",
% x[r1,c1] != x[r2,c2]
% )
% ));
include "alldifferent_except_0.mzn";
constraint alldifferent_except_0([x[r,c] | r in ROW, c in COL]);
% all soldiers get a position
%constraint forall(s in SOLDIER)(exists(r in ROW, c in COL)(r <= nrow /\ c <= ncol /\ x[r,c] = s));
%include "global_cardinality_low_up.mzn";
%constraint global_cardinality_low_up([x[r,c] | r in ROW, c in COL],
% [s | s in SOLDIER], [1 | s in SOLDIER], [1| s in SOLDIER]);
constraint sum(r in ROW, c in COL)(x[r,c] != 0) = nsoldier;
% no straw soldier has only soldiers of less or equal height in front of them
%constraint not exists(r1 in ROW, c in COL)
% (r1 in 1..nrow /\ c in 1..ncol /\ x[r1,c] = 0 /\
% forall(r2 in ROW)(r2 < r1 -> (x[r2,c] = 0 \/
% height[x[r2,c]] <= strawheight)));
array[SOLDIER0] of int: heightx = array1d(SOLDIER0,[strawheight] ++ height);
%constraint not exists(r1 in ROW, c in COL)
% (r1 in 1..nrow /\ c in 1..ncol /\ x[r1,c] = 0 /\
% forall(r2 in ROW)(r2 < r1 -> heightx[x[r2,c]] <= strawheight));
constraint forall(r1 in ROW, c in COL)
(r1 in 1..nrow /\ c in 1..ncol /\ x[r1,c] = 0 ->
exists(r2 in ROW)(r2 < r1 /\ heightx[x[r2,c]] > strawheight));
% Each straw soldier has a real soldier adjacent
constraint forall(r in ROW, c in COL)
((r <= nrow /\ c <= ncol /\ x[r,c] = 0) ->
( if c < maxc then x[r,c+1] != 0 else false endif
\/ if c > 1 then x[r,c-1] != 0 else false endif
\/ if r < maxr then x[r+1,c] != 0 else false endif
\/ if r > 1 then x[r-1,c] != 0 else false endif));
% Each soldier has enough strength to support the straw soldiers
%constraint forall(r in ROW, c in COL)
% (x[r,c] > 0 -> sum(r1 in max(1,r-1)..min(maxr,r+1), c1 in max(1,c-1)..min(maxc,c+1))
% (r <= nrow /\ c <= ncol /\ x[r,c] = 0) < strength[x[r,c]]);
% minimize the sum of height differences in each row
%set of int: DIFF = 0..max(height);
%
%array[ROW,COL] of var DIFF: hd;
%constraint forall(r in ROW)
% (forall(c in 1..ncol-1)
% (if r > nrow \/ c > ncol then
% hd[r,c] = 0
% else if x[r,c] = 0 then
% if x[r,c+1] = 0 then
% hd[r,c] = 0
% else hd[r,c] = abs(strawheight - height[x[r,c+1]])
% endif
% else if x[r,c+1] = 0 then
% hd[r,c] = abs(height[x[r,c]] - strawheight)
% else hd[r,c] = abs(height[x[r,c]] - height[x[r,c+1]])
% endif
% endif
% endif));
%constraint forall(c in COL)(hd[nrow,c] = 0);
%array[ROW,1..maxc-1] of var DIFF: hd;
%constraint forall(r in ROW)
% (forall(c in 1..ncol-1)
% (if x[r,c] != 0 /\ x[r,c+1] != 0
% then hd[r,c] = abs(height[x[r,c]] - height[x[r,c+1]])
% else hd[r,c] = 0
% endif));
%constraint forall(r in ROW)
% (forall(c in 1..ncol-1)
% (hd[r,c] = if x[r,c] != 0 /\ x[r,c+1] != 0
% then abs(height[x[r,c]] - height[x[r,c+1]])
% else 0
% endif));
%constraint forall(r in ROW)
% (forall(c in 1..ncol-1)
% (hd[r,c] = (x[r,c] != 0 /\ x[r,c+1] != 0)*abs(heightx[x[r,c]] - heightx[x[r,c+1]])));
%var int: obj = sum(r in ROW,c in 1..maxc-1)(hd[r,c]);
solve maximize nrow*ncol;
output [ if fix(x[r,c]) = 0 then " ." else show_int(2,height[x[r,c]]) endif ++
if c = maxc then "\n" else " " endif | r in ROW, c in COL]
++ ["x = array2d(ROW,COL,\(x));\n"]
++ ["nrow = \(nrow);\nncol = \(ncol);\n"]
% ++ ["hd = \(hd);\n"]
% ++ ["obj = \(obj);\n"]
;
寫在最後,一個問題有很多種建模的方法,但是如何建立一個高效率的模型非常的重要。在minizinc 中我們有很多中工具幫助我們建立模型,但是這種工具都不能處理規模較大的問題。比如exist 函式,推斷函式,等等,這些工具在那些商用的求解器Gurobi中是沒有的。
