文章轉自： https://www.cnblogs.com/fionacai/p/5894142.html

   首先，在瞭解樹模型之前，自然想到樹模型和線性模型有什麼區別呢？其中最重要的是，樹形模型是一個一個特徵進行處理，之前線性模型是所有特徵給予權重相加得到一個新的值。決策樹與邏輯迴歸的分類區別也在於此，邏輯迴歸是將所有特徵變換為概率後，通過大於某一概率閾值的劃分為一類，小於某一概率閾值的為另一類；而決策樹是對每一個特徵做一個劃分。另外邏輯迴歸只能找到線性分割（輸入特徵x與logit之間是線性的，除非對x進行多維對映），而決策樹可以找到非線性分割。

而樹形模型更加接近人的思維方式，可以產生視覺化的分類規則，產生的模型具有可解釋性（可以抽取規則）。

樹模型擬合出來的函式其實是分割槽間的階梯函式。

決策樹學習：採用自頂向下的遞迴的方法，基本思想是以資訊熵為度量構造一棵熵值下降最快的樹，到葉子節點處熵值為0（葉節點中的例項都屬於一類）。

  其次，需要了解幾個重要的基本概念：根節點（最重要的特徵）；父節點與子節點是一對，先有父節點，才會有子節點；葉節點（最終標籤）。

一、決策樹

決策樹生成的數學表示式：

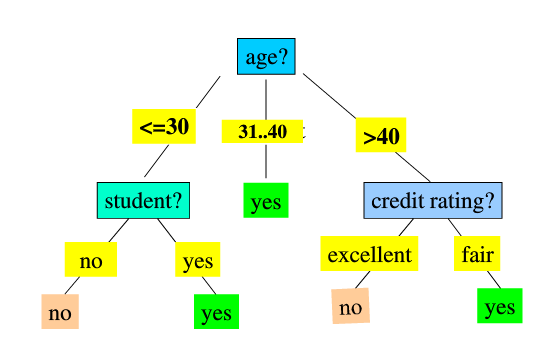
決策樹的生成：

決策樹思想，實際上就是尋找最純淨的劃分方法，這個最純淨在數學上叫純度，純度通俗點理解就是目標變數要分得足夠開（y=1的和y=0的混到一起就會不純）。另一種理解是分類誤差率的一種衡量。實際決策樹演算法往往用到的是，純度的另一面也即不純度，下面是不純度的公式。不純度的選取有多種方法，每種方法也就形成了不同的決策樹方法，比如ID3

演算法使用資訊增益作為不純度；C4.5演算法使用資訊增益率作為不純度；CART演算法使用基尼係數作為不純度。

決策樹要達到尋找最純淨劃分的目標要幹兩件事，建樹和剪枝

建樹：

（1）如何按次序選擇屬性

也就是首先樹根上以及樹節點是哪個變數呢？這些變數是從最重要到次重要依次排序的，那怎麼衡量這些變數的重要性呢？　ID3演算法用的是資訊增益，C4.5演算法用資訊增益率；CART演算法使用基尼係數。決策樹方法是會把每個特徵都試一遍，然後選取那個，能夠使分類分的最好的特徵，也就是說將A屬性作為父節點，產生的純度增益（GainA）要大於B屬性作為父節點，則A作為優先選取的屬性。

 

（根據log(x)的函式可知，p值越小，熵越大，所以當分組完全是會出現p=0此時熵最大）

（2） 如何分裂訓練資料（對每個屬性選擇最優的分割點）

如何分裂資料也即分裂準則是什麼？依然是通過不純度來分裂資料的，通過比較劃分前後的不純度值，來確定如何分裂。

下面做具體的介紹：

——CART演算法：既可以做分類，也可以做迴歸。只能形成二叉樹。

分支條件：二分類問題

分支方法：對於連續特徵的情況：比較閾值，高於某個閾值就屬於某一類，低於某個閾值屬於另一類。對於離散特徵：抽取子特徵，比如顏值這個特徵，有帥、醜、中等三個水平，可以先分為帥和不帥的，不帥的裡面再分成醜和中等的。

得分函式（y）：就是上面提到的gt(x)，對於分類樹取得是分類最多的那個結果（也即眾數），對於迴歸樹取得是均值。

損失函式：其實這裡的損失函式，就是分類的準則，也就是求最優化的準則

對於分類樹（目標變數為離散變數）：同一層所有分支假設函式的基尼係數的平均。

對於迴歸樹（目標變數為連續變數）：同一層所有分支假設函式的平方差損失

對於分類樹（目標變數為離散變數）：使用基尼係數作為分裂規則。比較分裂前的gini和分裂後的gini減少多少，減少的越多，則選取該分裂規則，這裡的求解方法只能是離散窮舉。關於基尼係數，可以參考周志華的西瓜書決策樹那章，講得比較簡潔，也比較易懂。“直觀來說，（資料集D的基尼係數）Gini(D)反映了從資料集D中隨機抽取兩個樣本，其類別標記不一致的概率，因此Gini(D)越小，則資料集D的純度越高。”

具體這個的計算，我覺得有例子才好理解，下面這個紅綠球的例子很好的說明了，如何根據損失函式最小（也就是基尼係數最小）來選取分裂規則。最後GIINs2更小，因此選擇它作為分類規則。

對於迴歸樹（目標變數為連續變數）：使用最小方差作為分裂規則。只能生成二叉樹。

CART與邏輯迴歸的比較：

主要優缺點如下圖。缺點補充幾點，不是很穩點，資料變化一點，你的樹就會發生變化；沒有考慮變數之間相關性，每次篩選都只考慮一個變數（因此不需要歸一化）；只能線性分割資料；貪婪演算法（可能找不到最好的樹）。優點也補充三點，同時可以處理分類變數和數值變數（但是可能決策樹對連續變數的劃分並不合理，所以可以提前先離散化）；可以處理多輸出問題；另外決策樹不需要做變數篩選，它會自動篩選；適合處理高維度資料。

ID3演算法：使用資訊增益作為分裂的規則，資訊增益越大，則選取該分裂規則。多分叉樹。資訊增益可以理解為，有了x以後對於標籤p的不確定性的減少，減少的越多越好，即資訊增益越大越好。

C4.5演算法：使用資訊增益率作為分裂規則（需要用資訊增益除以，該屬性本身的熵），此方法避免了ID3演算法中的歸納偏置問題，因為ID3演算法會偏向於選擇類別較多的屬性（形成分支較多會導致資訊增益大）。多分叉樹。連續屬性的分裂只能二分裂，離散屬性的分裂可以多分裂，比較分裂前後資訊增益率，選取資訊增益率最大的。

三種方法對比：

ID3的缺點，傾向於選擇水平數量較多的變數，可能導致訓練得到一個龐大且深度淺的樹；另外輸入變數必須是分類變數（連續變數必須離散化）；最後無法處理空值。

C4.5選擇了資訊增益率替代資訊增益。

CART以基尼係數替代熵；最小化不純度而不是最大化資訊增益。

剪樹：

（2） 如何停止分裂

   下面這六種情況都會停止分裂。其中第一種其實屬於樹的完全長成，但這會出現過擬合問題，所有之前很流行一種抑制這種情況的方法，叫樹的剪枝。樹的剪枝分為預剪枝和後剪枝，預剪枝，及早的停止樹增長控制樹的規模，方法可以參考如下6點停止分類的條件。後剪枝在已生成過擬合決策樹上進行剪枝，刪除沒有意義的組，可以得到簡化版的剪枝決策樹，包括REP（設定一定的誤分類率，減掉對誤分類率上升不超過閾值的多餘樹）、PEP，還有一種CCP，即給分裂準則—基尼係數加上懲罰項，此時樹的層數越深，基尼係數的懲罰項會越大。

 

二、隨機森林

 儘管有剪枝等等方法，一棵樹的生成肯定還是不如多棵樹，因此就有了隨機森林，解決決策樹泛化能力弱的缺點。（可以理解成三個臭皮匠頂過諸葛亮）

而同一批資料，用同樣的演算法只能產生一棵樹，這時Bagging策略可以幫助我們產生不同的資料集。Bagging策略來源於bootstrap aggregation：從樣本集（假設樣本集N個數據點）中重取樣選出Nb個樣本（有放回的取樣，樣本資料點個數仍然不變為N），在所有樣本上，對這n個樣本建立分類器（ID3\C4.5\CART\SVM\LOGISTIC），重複以上兩步m次，獲得m個分類器，最後根據這m個分類器的投票結果，決定資料屬於哪一類。

隨機森林在bagging的基礎上更進一步：

1.  樣本的隨機：從樣本集中用Bootstrap隨機選取n個樣本

2.  特徵的隨機：從所有屬性中隨機選取K個屬性，選擇最佳分割屬性作為節點建立CART決策樹（泛化的理解，這裡面也可以是其他型別的分類器，比如SVM、Logistics）

3.  重複以上兩步m次，即建立了m棵CART決策樹

4.  這m個CART形成隨機森林，通過投票表決結果，決定資料屬於哪一類（投票機制有一票否決制、少數服從多數、加權多數）

 

關於調參：1.如何選取K，可以考慮有N個屬性，取K=根號N

               2.最大深度（不超過8層）

               3.棵數

               4.最小分裂樣本樹

               5.類別比例

 

三、python實現程式碼

 

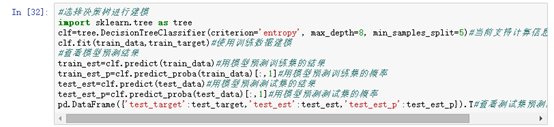
決策樹的重要引數都是防止過擬合的. 有2個引數是關鍵，min_samples_leaf 這個sklearn的預設值是1，經驗上必須大於100，如果一個節點都沒有100個樣本支援他的決策，一般都被認為是過擬合；max_depth 這個引數控制樹的規模。決策樹是一個非常直觀的機器學習方法。一般我們都會把它的決策樹結構打印出來觀察，如果深度太深對於我們的理解是有難度的。

 

分類: 資料探勘及演算法 好文要頂 關注我 收藏該文 fionaplanet
關注 - 9
粉絲 - 56 +加關注 7 0 « 上一篇： 聚類演算法
» 下一篇： 神經網路（1）

   首先，在瞭解樹模型之前，自然想到樹模型和線性模型有什麼區別呢？其中最重要的是，樹形模型是一個一個特徵進行處理，之前線性模型是所有特徵給予權重相加得到一個新的值。決策樹與邏輯迴歸的分類區別也在於此，邏輯迴歸是將所有特徵變換為概率後，通過大於某一概率閾值的劃分為一類，小於某一概率閾值的為另一類；而決策樹是對每一個特徵做一個劃分。另外邏輯迴歸只能找到線性分割（輸入特徵x與logit之間是線性的，除非對x進行多維對映），而決策樹可以找到非線性分割。

而樹形模型更加接近人的思維方式，可以產生視覺化的分類規則，產生的模型具有可解釋性（可以抽取規則）。樹模型擬合出來的函式其實是分割槽間的階梯函式。

決策樹學習：採用自頂向下的遞迴的方法，基本思想是以資訊熵為度量構造一棵熵值下降最快的樹，到葉子節點處熵值為0（葉節點中的例項都屬於一類）。

  其次，需要了解幾個重要的基本概念：根節點（最重要的特徵）；父節點與子節點是一對，先有父節點，才會有子節點；葉節點（最終標籤）。

一、決策樹

決策樹生成的數學表示式：

決策樹的生成：

決策樹思想，實際上就是尋找最純淨的劃分方法，這個最純淨在數學上叫純度，純度通俗點理解就是目標變數要分得足夠開（y=1的和y=0的混到一起就會不純）。另一種理解是分類誤差率的一種衡量。實際決策樹演算法往往用到的是，純度的另一面也即不純度，下面是不純度的公式。不純度的選取有多種方法，每種方法也就形成了不同的決策樹方法，比如ID3演算法使用資訊增益作為不純度；C4.5演算法使用資訊增益率作為不純度；CART演算法使用基尼係數作為不純度。

決策樹要達到尋找最純淨劃分的目標要幹兩件事，建樹和剪枝

建樹：

（1）如何按次序選擇屬性

也就是首先樹根上以及樹節點是哪個變數呢？這些變數是從最重要到次重要依次排序的，那怎麼衡量這些變數的重要性呢？　ID3演算法用的是資訊增益，C4.5演算法用資訊增益率；CART演算法使用基尼係數。決策樹方法是會把每個特徵都試一遍，然後選取那個，能夠使分類分的最好的特徵，也就是說將A屬性作為父節點，產生的純度增益（GainA）要大於B屬性作為父節點，則A作為優先選取的屬性。

 

（根據log(x)的函式可知，p值越小，熵越大，所以當分組完全是會出現p=0此時熵最大）

（2） 如何分裂訓練資料（對每個屬性選擇最優的分割點）

如何分裂資料也即分裂準則是什麼？依然是通過不純度來分裂資料的，通過比較劃分前後的不純度值，來確定如何分裂。

下面做具體的介紹：

——CART演算法：既可以做分類，也可以做迴歸。只能形成二叉樹。

分支條件：二分類問題

分支方法：對於連續特徵的情況：比較閾值，高於某個閾值就屬於某一類，低於某個閾值屬於另一類。對於離散特徵：抽取子特徵，比如顏值這個特徵，有帥、醜、中等三個水平，可以先分為帥和不帥的，不帥的裡面再分成醜和中等的。

得分函式（y）：就是上面提到的gt(x)，對於分類樹取得是分類最多的那個結果（也即眾數），對於迴歸樹取得是均值。

損失函式：其實這裡的損失函式，就是分類的準則，也就是求最優化的準則

對於分類樹（目標變數為離散變數）：同一層所有分支假設函式的基尼係數的平均。

對於迴歸樹（目標變數為連續變數）：同一層所有分支假設函式的平方差損失

對於分類樹（目標變數為離散變數）：使用基尼係數作為分裂規則。比較分裂前的gini和分裂後的gini減少多少，減少的越多，則選取該分裂規則，這裡的求解方法只能是離散窮舉。關於基尼係數，可以參考周志華的西瓜書決策樹那章，講得比較簡潔，也比較易懂。“直觀來說，（資料集D的基尼係數）Gini(D)反映了從資料集D中隨機抽取兩個樣本，其類別標記不一致的概率，因此Gini(D)越小，則資料集D的純度越高。”

具體這個的計算，我覺得有例子才好理解，下面這個紅綠球的例子很好的說明了，如何根據損失函式最小（也就是基尼係數最小）來選取分裂規則。最後GIINs2更小，因此選擇它作為分類規則。

對於迴歸樹（目標變數為連續變數）：使用最小方差作為分裂規則。只能生成二叉樹。

CART與邏輯迴歸的比較：

主要優缺點如下圖。缺點補充幾點，不是很穩點，資料變化一點，你的樹就會發生變化；沒有考慮變數之間相關性，每次篩選都只考慮一個變數（因此不需要歸一化）；只能線性分割資料；貪婪演算法（可能找不到最好的樹）。優點也補充三點，同時可以處理分類變數和數值變數（但是可能決策樹對連續變數的劃分並不合理，所以可以提前先離散化）；可以處理多輸出問題；另外決策樹不需要做變數篩選，它會自動篩選；適合處理高維度資料。

ID3演算法：使用資訊增益作為分裂的規則，資訊增益越大，則選取該分裂規則。多分叉樹。資訊增益可以理解為，有了x以後對於標籤p的不確定性的減少，減少的越多越好，即資訊增益越大越好。

C4.5演算法：使用資訊增益率作為分裂規則（需要用資訊增益除以，該屬性本身的熵），此方法避免了ID3演算法中的歸納偏置問題，因為ID3演算法會偏向於選擇類別較多的屬性（形成分支較多會導致資訊增益大）。多分叉樹。連續屬性的分裂只能二分裂，離散屬性的分裂可以多分裂，比較分裂前後資訊增益率，選取資訊增益率最大的。

三種方法對比：

ID3的缺點，傾向於選擇水平數量較多的變數，可能導致訓練得到一個龐大且深度淺的樹；另外輸入變數必須是分類變數（連續變數必須離散化）；最後無法處理空值。

C4.5選擇了資訊增益率替代資訊增益。

CART以基尼係數替代熵；最小化不純度而不是最大化資訊增益。

剪樹：

（2） 如何停止分裂

   下面這六種情況都會停止分裂。其中第一種其實屬於樹的完全長成，但這會出現過擬合問題，所有之前很流行一種抑制這種情況的方法，叫樹的剪枝。樹的剪枝分為預剪枝和後剪枝，預剪枝，及早的停止樹增長控制樹的規模，方法可以參考如下6點停止分類的條件。後剪枝在已生成過擬合決策樹上進行剪枝，刪除沒有意義的組，可以得到簡化版的剪枝決策樹，包括REP（設定一定的誤分類率，減掉對誤分類率上升不超過閾值的多餘樹）、PEP，還有一種CCP，即給分裂準則—基尼係數加上懲罰項，此時樹的層數越深，基尼係數的懲罰項會越大。

 

二、隨機森林

 儘管有剪枝等等方法，一棵樹的生成肯定還是不如多棵樹，因此就有了隨機森林，解決決策樹泛化能力弱的缺點。（可以理解成三個臭皮匠頂過諸葛亮）

而同一批資料，用同樣的演算法只能產生一棵樹，這時Bagging策略可以幫助我們產生不同的資料集。Bagging策略來源於bootstrap aggregation：從樣本集（假設樣本集N個數據點）中重取樣選出Nb個樣本（有放回的取樣，樣本資料點個數仍然不變為N），在所有樣本上，對這n個樣本建立分類器（ID3\C4.5\CART\SVM\LOGISTIC），重複以上兩步m次，獲得m個分類器，最後根據這m個分類器的投票結果，決定資料屬於哪一類。

隨機森林在bagging的基礎上更進一步：

1.  樣本的隨機：從樣本集中用Bootstrap隨機選取n個樣本

2.  特徵的隨機：從所有屬性中隨機選取K個屬性，選擇最佳分割屬性作為節點建立CART決策樹（泛化的理解，這裡面也可以是其他型別的分類器，比如SVM、Logistics）

3.  重複以上兩步m次，即建立了m棵CART決策樹

4.  這m個CART形成隨機森林，通過投票表決結果，決定資料屬於哪一類（投票機制有一票否決制、少數服從多數、加權多數）

 

關於調參：1.如何選取K，可以考慮有N個屬性，取K=根號N

               2.最大深度（不超過8層）

               3.棵數

               4.最小分裂樣本樹

               5.類別比例

 

三、python實現程式碼

 

決策樹的重要引數都是防止過擬合的. 有2個引數是關鍵，min_samples_leaf 這個sklearn的預設值是1，經驗上必須大於100，如果一個節點都沒有100個樣本支援他的決策，一般都被認為是過擬合；max_depth 這個引數控制樹的規模。決策樹是一個非常直觀的機器學習方法。一般我們都會把它的決策樹結構打印出來觀察，如果深度太深對於我們的理解是有難度的。