這一篇首先會說說前面剩餘的一點知識2-3樹，然後簡單說說B樹，不寫程式碼，只是簡單看看原理吧！

　　為什麼要說一下2-3樹呢？瞭解2-3樹之後能更快的瞭解B樹；

1.簡單看看2-3樹

　　其實我們學過了前面的2-3-4樹之後，再看2-3樹就太容易了，2-3樹中任意一個節點最多隻有三個子節點，而且節點中只有兩個空位置可以存資料；除了分裂，其他的都和2-3-4樹一樣的，就不多說了，下面我們就隨意看看節點分裂吧！

　　首先要區分2-3-4樹和2-3樹分裂的的不同，對於2-3-4樹來說是插入資料之前首先會把滿的葉節點分裂，把三個資料分配完了之後再插入資料到節點中；而對於2-3樹來說，是在插入期間，什麼是插入期間呢？看看下圖：

　　上圖中的操作的目的就是向2-3樹中插入85，插入的時候會判斷該葉節點是不是滿的，假如是滿的 ，首先就80、90、85進行從小到大排列 為80、85、90，然後80不動，中間的資料放進父節點中，最後將90放入新建立的節點當中，就ok了；這裡假如85在進入父節點的時候發現父節點滿了，那麼父節點就會分裂，這裡跟2-3-4樹差不多，重複上述步驟，左邊資料不動，將中間值放入父節點，右邊資料放入新建節點；說起來很繞，請看下圖：

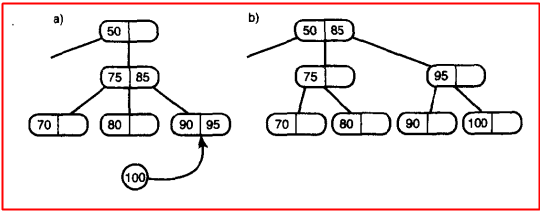
　　其實沒什麼新的東西，弄懂了2-3-4樹，再看2-3樹幾分鐘就差不多了，這裡也就是隨意看看，有興趣的可以用程式碼實現一下，這裡就是注意一下2-3樹和2-3-4樹分裂過程的不同就可以了；

2.硬碟儲存資料

　　我們前面說的所有資料結構都是存在於記憶體中的，當電腦一關機記憶體就會全部釋放，所有的資料結構都會消失；但是有沒有想過硬碟中是怎麼存資料的啊？

　　於是就有了B樹，屬於一種多叉樹，在外部儲存器存資料的時候起很大的作用，外部儲存暫時就理解為硬碟即可！話說資料為什麼要存到硬碟中呢？最大的有點就是硬碟便宜，而且硬碟空間比記憶體大得多，可以存很多很多的資料，而且硬碟最大的優點就是可以持久化，就是電腦即使關機了，資料還是存在硬碟中不會消失；

　　但是存在硬碟中有個很大的問題，就是從硬碟中讀取資料的時候太慢太慢了，而從記憶體中讀取資料的速度大概比硬碟讀取快幾萬倍，相差一個數量級；其實對於cpu的運算速度來說從記憶體中讀資料還是太慢了，於是就有了快取，後面有機會再說......

　　雖然每年硬碟技術都在提高，但是記憶體技術提高的更快，可以想象記憶體和硬碟的速度只會越來越大！

　　2.1找到硬碟中資料的正確位置

　　假設我們要存一個城市的電話記錄，大概50萬條資料，每條資料512個位元組，那麼總共應該是50萬x512=2億5千6百萬  位元組，差不多就是256M，這個肯定不能存在記憶體中，要想辦法把這256M的資料存到硬碟中還要保證我們從硬碟中查詢，插入和刪除指定記錄的速度要足夠快才行，不然使用者體驗太差了。。。

　　我們知道計算機想要讀取硬碟中的資料是通過驅動（其實就是磁碟驅動器）去對硬碟進行操作，硬碟內部如下圖所示，其實最終就是通過磁頭對碟片進行操作，但是怎麼操作呢？我們可以把碟片看作打靶的那個靶子一樣有很多個圈，磁頭首先要找到目標資料所在的圈（也叫做磁軌）需要幾毫秒，然後碟片需要旋轉一下磁頭才能在當前磁軌中找到正確的位置（平均下來是要旋轉半圈）需要幾毫秒，找到正確的位置後，最後就是實際的讀寫操作了，差不多也需要幾毫秒；假設硬碟這裡的所有操作共需要10毫秒（10^-3），而假如從記憶體中訪問正確的資料則只需要幾微秒（10^-9），可以看到速度相差了好多好多倍；

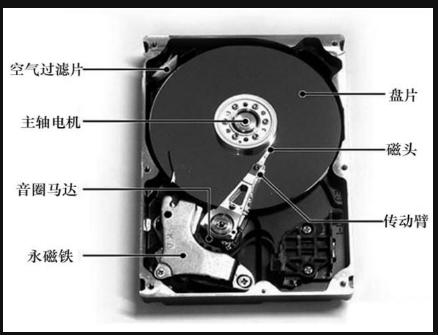
　　那肯定有人要問了，既然記憶體這麼快那幹嘛不直接用記憶體條當硬碟來用呢？emmm....最主要的原因就是記憶體條很貴啊，你可以去淘寶或者京東查查幾個G的記憶體條多少RMB，至少好幾百，我們電腦儲存量至少也要五六百個G吧，於是你買記憶體條就可以破產了；但是硬碟的話1T也就一兩百塊，價格才是最主要的。

　　2.2.讀取資料塊

　　磁頭在硬碟的碟片中找到資料的正確位置了之後，難道要一條一條資料慢慢讀麼？當然不會用這麼愚蠢的方法，我們可以把碟片中的資料分成一塊一塊的，需要的時候直接讀取一塊資料到記憶體中的快取區，通常塊的大小和作業系統和磁碟驅動器的容量相關，而且必須是2的倍數，假設這裡我們把塊的大小設定為8192位元組（2¹³），那麼上面那兩億多個位元組的資料就變成31250塊；

　　塊分完之後，假設我們要讀取100位元組的資料，那麼磁碟驅動器首先直接讀取一塊資料，然後將這塊資料前100位元組留下其他的都扔了；假如是讀取8292位元組，那麼就會讀取兩塊資料，然後將第二塊資料留下100位元組就將第二塊資料其他的都扔了；

　　順便一說，上面說了一條資料512位元組，一塊資料是8192位元組，可以知道一塊資料其實就儲存有16條記錄，所以我們一次讀取16條資料效率是最高的，不需要對資料進行丟棄操作；

　　2.3.硬碟中資料有序

　　我們存到硬碟中的資料，可以是有序和無序的；

　　假如硬碟中的資料是無序的，那麼插入肯定是很快的，但是查詢就比較坑了，因為硬碟中這麼多資料要慢慢的進行遍歷，那就只能慢慢等等了。。。

　　假如硬碟中的資料是有序排列的，那麼我們去查詢一條記錄的時候就會很快，可以用二分法查詢，到底有多快呢？假如你要從50萬條資料中查詢某條資料，最多需要查詢19次，如果一次10微秒，那總共190微秒，比我們眨一下眼睛的時間還短；

　　二分法其實很容易的一個東西，舉個例子一個數組中有順序的資料0、1、2、3、4、5、6、7、8、9、10，我們要查詢9所在的位置！假如我們用遍歷那就需要10次；如果用二分法，首先9和中間的5比較，比5大，那就再和右半部分中間的8比較，比8大，繼續在右邊查詢，可以找到9，只需要三次操作，資料量越大二分法的效果越明顯；但是二分法也有缺陷就是必須要讓資料有序，這就導致插入（或刪除）的時候比較坑爹，就類似有序陣列的插入，插入一個數據之後就要將這個資料後面的所有都往後移動一個位置，而且資料越多插入的效率越糟糕；

　　回到硬碟中資料的儲存，假如我們將硬碟中的資料弄成有序的，分塊完了之後（後面操作是以塊為單位），查詢可以用二分查詢先找到某塊資料，讀取到磁碟驅動器的快取中，然後裡面就16條資料很快就可以找到；但是插入資料的話平均要移動一半的塊，每移動一個塊都需要一次硬碟的讀寫操作（就是都要經過2.1到2.2這個步驟然後把資料寫入硬碟，賊坑！），下面就隨意說說一次讀寫到底是怎麼做的；

　　假如我們現在要插入一條記錄A，第一步：首先會經過2.1和2.2讀取一塊資料並存在快取中，將這塊資料最後一條記錄儲存下來，然後判斷記錄A可以放在這塊資料的哪裡，適當移動這塊資料中記錄的位置並插入資料A，然後就把快取區中的這塊資料寫入磁碟中；第二步：讀取下一塊資料，也是儲存這塊資料的最後一條記錄，將這塊資料中的記錄都往後移動一個空位置，讓上一塊資料中儲存的最後的一條記錄插入到這塊的最開始的位置，然後將本塊資料寫入磁碟；這個第二步會一直重複，直到將所有記錄都重新寫入。。。

　　我們上面資料分塊是31250塊，假如每次讀寫都要10毫秒，那麼我們插入一條記錄差不多需要5分鐘，真是足夠坑爹！

3.簡單看看B樹

　　根據上面我們可以知道資料存到硬碟中是分為兩種情況的，但是兩種情況各有優缺點，那有沒有汲二者優點的儲存方式呢？聰明的大佬們早就想出來了，這就像陣列和連結串列的關係，最終我們引入了樹的概念完美解決了陣列和連結串列的缺陷，類似的現在我們在硬碟中也要引入一種樹來解決，這種樹就是B樹；

　　B樹是一種多叉樹，也有人稱為B-樹，其實就是一種樹！有點類似2-3-4樹，只是B樹每個節點都有很多個節點，那到底可以是多少個呢？我們慢慢看，補充一點，前面我們學習過的2-3樹和2-3-4樹都只是B樹的兩種特殊情況，如果對這兩種樹不熟悉的一定要先去看看；

　　根據前面的2-3-4樹可以知道一個非葉節點的子節點數目 = 節點資料項+1，在B樹中也是這樣；還有，既然都說了2-3樹和2-3-4樹都只是B樹的特殊情況，那就可以猜到B樹的節點中的資料估計有很多個，我們該怎麼選取節點才是最高效的呢？還記得前面說的分塊嗎，我們這裡就是將一塊資料作為一個節點；

　　我們再回顧一下上面說的城市的電話記錄的例子，總共有2億5千6百萬位元組，一條記錄512位元組，根據每一塊資料8192位元組（16條記錄）進行分塊，可以分為31250塊，換句話說每塊資料中存有16條資料，這就有點意思了，我們把每16條記錄看作B樹的一個節點的資料項，那麼就應該有17個子節點才對；我們還知道每一個節點要儲存子節點的引用，怎麼做比較好呢？比較奢侈的做法是：讓每個節點只儲存15條記錄，還有一條記錄大小的空間用於存放子節點和父節點的引用吧！此時只有16個子節點；但是比較高效的做法是：一個節點中最好存偶數個數據，然後適當縮小每條記錄的大小為507個位元組，那麼每一塊中16條資料會佔用8112位元組，還剩下80位元組，我們有17個子節點，每個子節點引用時int型別(一個int資料佔4個位元組)的資料，17x4=68 < 80，說明節點空間中即使儲存子節點引用還是夠用，下圖所示：

　　下面我們簡單說說B樹的一些基本操作，不用程式碼來表示的，瞭解原理即可；

　　3.1 查詢

　　這個查詢的操作和2-3-4樹差不多，就是子節點多了很多而已，很容易！首先將根節點資料讀到記憶體中，然後根據搜尋演算法對這個節點進行搜尋，從0開始，其實就是比較在哪個範圍下，然後繼續到對應的子節點那裡去找。。。重複這個步驟就能找到目的資料；

　　3.2 插入

　　插入這個操作就跟2-3樹差不多了，為什麼不用2-3-4樹那樣的插入方式呢？因為我們可以知道2-3-4樹中的節點很多都是沒有放滿的，有很多節點只存了一個數據，有太多空位置，假如B樹用這樣的方式硬碟中會很浪費空間，而用類似2-3樹這種方式利用率就比較高，我們可以看看B樹中是怎麼分裂的；

·　　在插入資料的時候，假設該節點已經滿了，我們還要向其中插入一個數據下圖所示；

　　我們將70和節點中的資料進行從小到大排列，然後以中間資料60為界限，左邊的資料不動，中間資料60放入父節點（根節點比較特殊，要新建一個父節點），右邊的資料放入新建的節點：

　　繼續插入18、30、15，過程如下，比較類似2-3樹的分裂，沒什麼特別不好理解的，只是子節點比較多而已

　　最後看一個比較複雜的節點分裂，其實跟前面差不多。。。

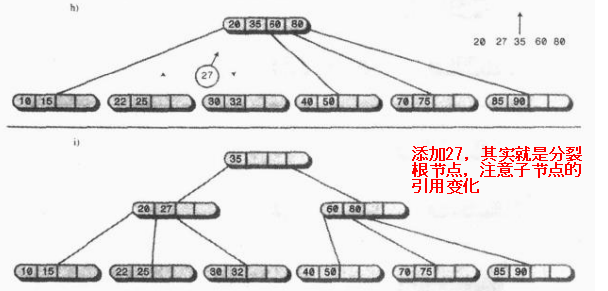
　　可以簡單看到B樹中，除了根節點之外，其他的節點最低也會用一半的空間，利用率最低也是50%，這就已經很可以了；

4.B樹效率

　　B樹的效率如何呢？空間利用率還行，我們還是以最開始的那個城市電話記錄為例子簡單說說，總共有50萬條記錄以B樹的形式存在硬碟中，每個節點至少也是半滿，我們就以每個節點裝滿一半資料計算，可以算出樹的高度大概為6，每個節點有8條記錄（對應9個子節點）；

　　至於到底怎麼計算的，感覺沒什麼好說的，B樹節點存資料的大小（或者說的塊資料）是一定的，跟作業系統等因素有關，我們這裡為16，每個節點存一半就是存8條資料，擁有9個子節點，是在不行用計算器算一下樹的高度最低要為6才能存滿50萬資料，雖然我是對於這種計算的東西沒多大興趣。。。

　　由於樹只有6層，那麼我們查詢任意一條資料也就需要6次比較而已，假設每次為10毫秒，那麼最多就花費60毫秒，6/100秒；你想想從50萬條資料中任意查詢一條記錄最多是6/100秒，這個效率已經很ok了，雖然查詢效率已經很不錯了，但是插入和刪除操作才能顯示出B樹的最大優越性；

 　　就比如說插入，假如插入資料到葉節點中，該葉節點沒有滿，那就不需要進行分裂，也就需要對硬碟7次操作，前六次是比較使得找到正確節點，第7次就是讀取葉節點資料到快取，插入資料然後寫入硬碟；假如插入資料之後葉節點要進行分裂的話，找到葉節點、移動節點中的資料和建立新的節點等操作合在一起也就需要對硬碟的12步操作，這效率很厲害了，不能再多說了，這篇已經足夠長了。。。

5.總結

　　B樹其實也就這樣吧，可能是沒有仔細實現B樹程式碼，但是感覺還行，最複雜的還是分裂這裡，不過也就和2-3-4樹差不了多少！

　　其實B樹有很多種，我們常說的B樹和B-樹是一樣的，還有B+樹、B*樹；其中B+樹是對B-樹的一個改進（多應用於作業系統索引和資料庫索引），B*樹又是對B+樹的一個改進，瞭解了B-樹之後再看後面這兩種樹很容易的，無非是增加幾個指標，提高了節點利用率什麼的，後面有時間再說吧！話說還有個R樹，emmm....需要的時候再去看