An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.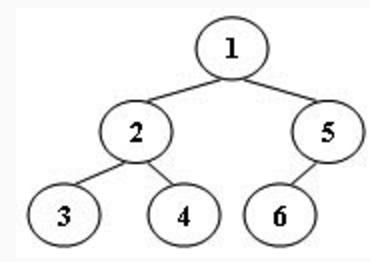

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (<=30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: “Push X” where X is the index of the node being pushed onto the stack; or “Pop” meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:
6
Push 1
Push 2

題目大意：用棧的形式給出一棵二叉樹的建立的順序，求這棵二叉樹的後序遍歷

需要一個堆結構s，一個child變數（表示該節點是其父親節點的左孩子還是右孩子），父親節點fa
對於push v操作：
1).第一個push肯定是根節點root。
2).根據child變數，建立fa與v的父子關係。
3).由於是中序遍歷，所以接下來的節點必定是v的left（如果有的話），child=left,fa=v;
4).然後進行push操作

對於pop操作：
1).根據中序遍歷性質，可知接下來的節點必定是pop節點的右孩子（如果有的話）,child=right,fa=s.top()
2).進行pop操作。

#include<iostream>
#include<algorithm>
#include<string.h>
#include<stack>
#define LEFT 0
#define RIGHT 1
#define maxn 100
using namespace std;
stack<int> s;
//著重注意這題考查的是"建樹"的技巧 
struct  NODE
{
   int left=-1;	
   int right=-1;	 
}node[maxn];

bool first=true;
void postOrder(int u){//雖然建樹時是按中序建的樹
    if(u==-1)         //但是按後序掃的
        return;
    postOrder(node[u].left);
    postOrder(node[u].right);
    if(first){
        first=false;
        printf("%d",u);
    }
    else{
        printf(" %d",u);
    }
}

int main()
{
	int n,v;
	int root=-1,fa;
	//fa是為了記錄當前結點
	//以便把各個node結點相連 
	int child=LEFT;
	//child變數記錄的是,
	//當前父節點往左走，還是往右走 
	char str[10];
	scanf("%d",&n);
	while(scanf("%s",str)!=EOF)
	{
		if(strcmp(str,"Push")==0)
		{
			scanf("%d",&v);
			if(root==-1)//為這棵樹找根節點，入口 
			root=v;
			else 
			{
				if(child==LEFT)
                node[fa].left=v;
				else node[fa].right=v;				
			}
			fa=v;//更新父節點 
			child=LEFT;
			s.push(v); 
		}//對於入棧的操作,
		 //由於是中序，新節點優先進左子樹 
		else//出棧後在改變方向,
		    //再次push時向右子樹push 
		{
			child=RIGHT;
			fa=s.top(); 
			s.pop();
		}
	}
	postOrder(root);
    return 0;	
}