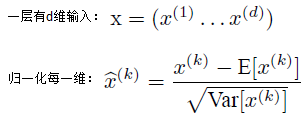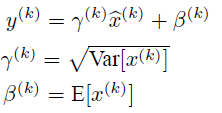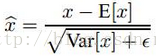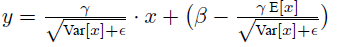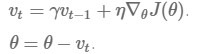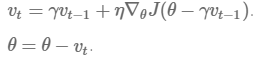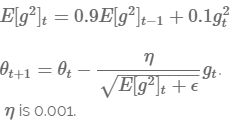深度學習技巧(啟用函式-BN-引數優化等等)
轉自https://blog.csdn.net/myarrow/article/details/51848285
1. 深度學習技巧簡介
1)一次性設定(One time setup)
- 啟用函式(Activation functions)
- 資料預處理(Data Preprocessing)
- 權重初始化(Weight Initialization)
- 正則化(Regularization:避免過擬合的一種技術)
- 梯度檢查(Gradient checking)
2)動態訓練(Training dynamics)
- 跟蹤學習過程 (Babysitting the learning process)
- 引數更新 (Parameter updates)
- 超級引數優化(Hyperparameter optimization)
- 批量歸一化(BN:Batch Normalization:解決在訓練過程中,中間層資料分佈發生改變的問題,以防止梯度消失或爆炸、加快訓練速度)
3)評估(Evaluation)
- 模型組合(Model ensembles)
(訓練多個獨立的模型,測試時,取這些模型結果的平均值)
神經網路學習過程本質就是為了:學習資料分佈,一旦訓練資料與測試資料的分佈不同,那麼網路的泛化能力也大大降低,所以需要使用輸入資料歸一化方法,使訓練資料與測試資料的分佈相同。
2. 啟用函式(Activation Functions)
詳細內容參見:啟用函式
總結:
1)使用ReLU時,使Learning Rates儘量小
2)嘗試使用Leaky ReLU/Maxout/ELU
3)可以使用tanh,但期望不要太高
4)不要使用sigmoid
3. 資料預算處理(Data Preprocessing)
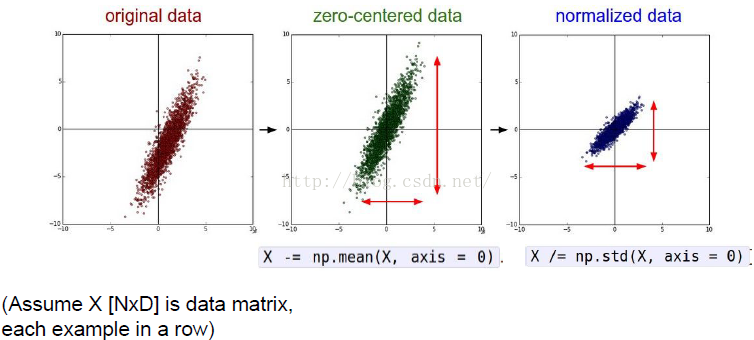
1)為什麼輸入資料需要歸一化(Normalized Data)?
歸一化後有什麼好處呢?原因在於神經網路學習過程本質就是為了學習資料分佈,一旦訓練資料與測試資料的分佈不同,那麼網路的泛化能力也大大降低;另外一方面,一旦每批訓練資料的分佈各不相同(batch 梯度下降),那麼網路就要在每次迭代都去學習適應不同的分佈,這樣將會大大降低網路的訓練速度,這也正是為什麼我們需要對資料都要做一個歸一化預處理的原因。
對於深度網路的訓練是一個複雜的過程,只要網路的前面幾層發生微小的改變,那麼後面幾層就會被累積放大下去。一旦網路某一層的輸入資料的分佈發生改變,那麼這一層網路就需要去適應學習這個新的資料分佈,所以如果訓練過程中,訓練資料的分佈一直在發生變化,那麼將會影響網路的訓練速度。
4. 權重初始化(Weight Initialization)
1)小的隨機數
w= 0.01 * np.random.randn(fan_in,fan_out)
2)神經元將飽和,梯度為0
w = 1.0 * np.random.randn(fan_in,fan_out)
3)合理的初始化(Xavier init)
w = np.random.randn((fan_in,fan_out)/np.sqrt(fan_in)
權重初始化是一個重要的研究領域。
5. 批量歸一化(BN: Batch Normalization)
5.1 BN訓練
1)隨機梯度下降法(SGD)對於訓練深度網路簡單高效,但是它有個毛病,就是需要我們人為的去選擇引數,比如學習率、引數初始化、權重衰減係數、Drop out比例等。這些引數的選擇對訓練結果至關重要,以至於我們很多時間都浪費在這些的調參上。那麼使用BN(詳見論文《Batch Normalization_ Accelerating Deep Network Training by Reducing Internal Covariate Shift》)之後,你可以不需要那麼刻意的慢慢調整引數。
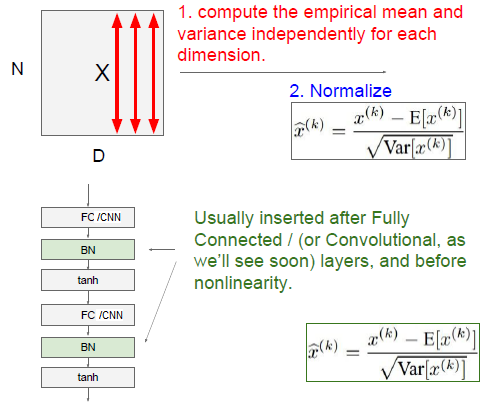
2)神經網路一旦訓練起來,那麼引數就要發生更新,除了輸入層的資料外(因為輸入層資料,我們已經人為的為每個樣本歸一化),後面網路每一層的輸入資料分佈是一直在發生變化的,因為在訓練的時候,前面層訓練引數的更新將導致後面層輸入資料分佈的變化。以網路第二層為例:網路的第二層輸入,是由第一層的引數和input計算得到的,而第一層的引數在整個訓練過程中一直在變化,因此必然會引起後面每一層輸入資料分佈的改變。我們把網路中間層在訓練過程中,資料分佈的改變稱之為:“Internal Covariate Shift”。Paper所提出的演算法,就是要解決在訓練過程中,中間層資料分佈發生改變的情況,於是就有了Batch Normalization,這個牛逼演算法的誕生。
3)BN的地位:與啟用函式層、卷積層、全連線層、池化層一樣,BN(Batch Normalization)也屬於網路的一層。
4)BN的本質原理:在網路的每一層輸入的時候,又插入了一個歸一化層,也就是先做一個歸一化處理(歸一化至:均值0、方差為1),然後再進入網路的下一層。不過文獻歸一化層,可不像我們想象的那麼簡單,它是一個可學習、有引數(γ、β)的網路層。
5)歸一化公式:
6)如果是僅僅使用上面的歸一化公式,對網路某一層A的輸出資料做歸一化,然後送入網路下一層B,這樣是會影響到本層網路A所學習到的特徵的。比如我網路中間某一層學習到特徵資料本身就分佈在S型啟用函式的兩側,你強制把它給我歸一化處理、標準差也限制在了1,把資料變換成分佈於s函式的中間部分,這樣就相當於我這一層網路所學習到的特徵分佈被你搞壞了,這可怎麼辦?於是文獻使出了一招驚天地泣鬼神的招式:變換重構,引入了可學習引數γ、β,這就是演算法關鍵之處:
上面的公式表明,通過學習到的重構引數γ、β,是可以恢復出原始的某一層所學到的特徵的。
7)引入了這個可學習重構引數γ、β,讓我們的網路可以學習恢復出原始網路所要學習的特徵分佈。最後Batch Normalization網路層的前向傳導過程公式就是:
8)BN層是對於每個神經元做歸一化處理,甚至只需要對某一個神經元進行歸一化,而不是對一整層網路的神經元進行歸一化。既然BN是對單個神經元的運算,那麼在CNN中卷積層上要怎麼搞?假如某一層卷積層有6個特徵圖,每個特徵圖的大小是100*100,這樣就相當於這一層網路有6*100*100個神經元,如果採用BN,就會有6*100*100個引數γ、β,這樣豈不是太恐怖了。因此卷積層上的BN使用,其實也是使用了類似權值共享的策略,把一整張特徵圖當做一個神經元進行處理。
9)卷積神經網路經過卷積後得到的是一系列的特徵圖,如果min-batch sizes為m,那麼網路某一層輸入資料可以表示為四維矩陣(m,f,w,h),m為min-batch sizes,f為特徵圖個數,w、h分別為特徵圖的寬高。在CNN中我們可以把每個特徵圖看成是一個特徵處理(一個神經元),因此在使用Batch Normalization,mini-batch size 的大小就是:m*w*h,於是對於每個特徵圖都只有一對可學習引數:γ、β。說白了吧,這就是相當於求取所有樣本所對應的一個特徵圖的所有神經元的平均值、方差,然後對這個特徵圖神經元做歸一化。
10) 在使用BN前,減小學習率、小心的權重初始化的目的是:使其輸出的資料分佈不要發生太大的變化。
11) BN的作用:
1)改善流經網路的梯度
2)允許更大的學習率,大幅提高訓練速度:
你可以選擇比較大的初始學習率,讓你的訓練速度飆漲。以前還需要慢慢調整學習率,甚至在網路訓練到一半的時候,還需要想著學習率進一步調小的比例選擇多少比較合適,現在我們可以採用初始很大的學習率,然後學習率的衰減速度也很大,因為這個演算法收斂很快。當然這個演算法即使你選擇了較小的學習率,也比以前的收斂速度快,因為它具有快速訓練收斂的特性;
3)減少對初始化的強烈依賴
4)改善正則化策略:作為正則化的一種形式,輕微減少了對dropout的需求
你再也不用去理會過擬閤中drop out、L2正則項引數的選擇問題,採用BN演算法後,你可以移除這兩項了引數,或者可以選擇更小的L2正則約束引數了,因為BN具有提高網路泛化能力的特性;
5)再也不需要使用使用區域性響應歸一化層了(區域性響應歸一化是Alexnet網路用到的方法,搞視覺的估計比較熟悉),因為BN本身就是一個歸一化網路層;
6)可以把訓練資料徹底打亂(防止每批訓練的時候,某一個樣本都經常被挑選到,文獻說這個可以提高1%的精度)。
注:以上為學習過程,在測試時,均值和方差(mean/std)不基於小批量進行計算, 可取訓練過程中的啟用值的均值。
5.2 BN測試
1)實際測試時,我們依然使用下面的公式:
這裡的均值和方差已經不是針對某一個Batch了,而是針對整個資料集而言。因此,在訓練過程中除了正常的前向傳播和反向求導之外,我們還要記錄每一個Batch的均值和方差,以便訓練完成之後按照下式計算整體的均值和方差:
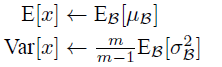
上面簡單理解就是:對於均值來說直接計算所有batch u值的平均值;然後對於標準偏差採用每個batch σB的無偏估計。最後測試階段,BN的使用公式就是:
2)BN可以應用於一個神經網路的任何神經元上。文獻主要是把BN變換,置於網路啟用函式層的前面。在沒有采用BN的時候,啟用函式層是這樣的:
z=g(Wu+b)
也就是我們希望一個啟用函式,比如s型函式s(x)的自變數x是經過BN處理後的結果。因此前向傳導的計算公式就應該是:
z=g(BN(Wu+b))
其實因為偏置引數b經過BN層後其實是沒有用的,最後也會被均值歸一化,當然BN層後面還有個β引數作為偏置項,所以b這個引數就可以不用了。因此最後把BN層+啟用函式層就變成了:
z=g(BN(Wu))
5.2 BN使用
為什麼BN層一般用線上性層和卷積層後面,而不是放在非線性單元后
原文中是這樣解釋的,因為非線性單元的輸出分佈形狀會在訓練過程中變化,歸一化無法消除他的方差偏移,相反的,全連線和卷積層的輸出一般是一個對稱,非稀疏的一個分佈,更加類似高斯分佈,對他們進行歸一化會產生更加穩定的分佈。其實想想也是的,像relu這樣的啟用函式,如果你輸入的資料是一個高斯分佈,經過他變換出來的資料能是一個什麼形狀?小於0的被抑制了,也就是分佈小於0的部分直接變成0了,這樣不是很高斯了。
6. 跟蹤訓練過程
1)Learning Rate
- Learning Rate太小(如1e-6),cost下降很慢
- Learning Rate太大(如1e-6),cost增長爆炸 (cur cost > 3* original cost)
- 在[1e-3,1e-5]範圍內比較合適
2)Mini-batch SGD
Loop:
1. Sample a batch of data
2. Forward prop it through the graph, get loss
3. Backprop to calculate the gradients
4. Update the parameters using gradient
7. 引數優化
引數優化的目的是:減少損失(loss), 直至損失收斂(convergence)
7.1 Gradient Descent Variants
7.1.1 Batch gradient descent
每次基於整個資料集計算梯度。
for i in range(nb_epochs):
params_grad = evaluate_gradient(loss_function, data, params)
params = params - learning_rate * params_grad7.1.2 SGD(Stochastic Gradient Descent: 隨機梯度下降)
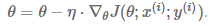
每次基於一個數據樣本計算梯度。
for i in range(nb_epochs):
np.random.shuffle(data)
for example in data:
params_grad = evaluate_gradient(loss_function, example, params)
params = params - learning_rate * params_grad7.1.3 Mini-batch Gradient Descent
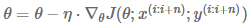
每次基於n個數據樣本計算梯度。
for i in range(nb_epochs):
np.random.shuffle(data)
for batch in get_batches(data, batch_size=50):
params_grad = evaluate_gradient(loss_function, batch, params)
params = params - learning_rate * params_grad優點:
1)減少引數更新的變化, 從而得到更加穩定的收斂
2)使用先進的Deep Learning庫,可以高效地計算mini-batch的梯度
注:n一般取[50,256]範圍內的數,視具體應用而定。
7.1.4 梯度下降演算法面臨的挑戰
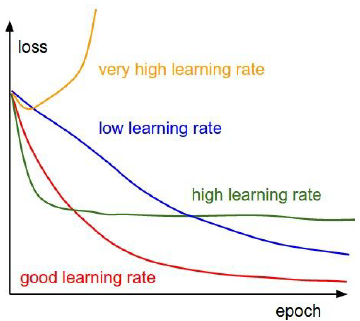
1)選擇合適的Learning Rate是困難的,太小導致收斂慢,太大阻礙收斂或且導致損失函式在最小值附近波動或發散;
2)預先定義的Learning Rate變動規則不能適應資料集的特性;
3)同樣的Learning Rate運用到所有的引數更新(後面的AdaGrad, AdaDelta, RMSProp, Adam為解決此問題而生);
4)最小化高度非凸損失函式的羝問題是:避免陷入眾多的區域性最優值。
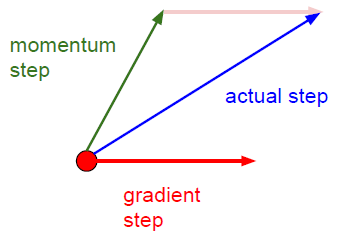
7.2 Momentum(動量)
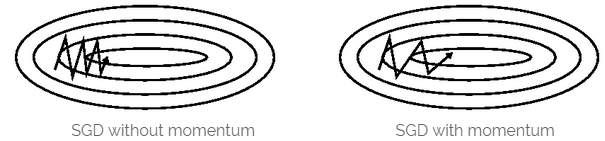
關鍵優點: 利用物體運動時的慣性,加快到達全域性最優點的速度,且減少振盪。
關鍵缺點:球盲目地沿著斜坡向山下滾。
當Loss function的表面曲線的一維比其它維有更多的溝壑時,SGD要跨越此溝壑是困難的,如上圖左邊所示,SGD沿著溝壑的斜坡振盪,然後猶猶豫豫地向區域性最優點前進。
Momentum即動量,它模擬的是物體運動時的慣性,即更新的時候在一定程度上保留之前更新的方向,同時利用當前batch的梯度微調最終的更新方向。這樣一來,可以在一定程度上增加穩定性,從而學習地更快,並且還有一定擺脫區域性最優的能力:
# Momentum update
V = gama * V + learning_rate * dw # integrate velocity
w -= V # integrate position 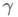
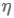
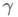
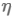
Momentum的物理解釋是:當我們把球推下山時,球不斷地累積其動量,速度越來越快(直到其最大速度,如果有空氣阻力,如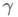
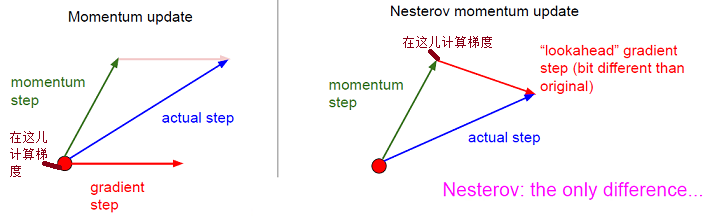
7.3 Nesterov Accelerated Gradient (NAG)
關鍵優點:一個聰明的球,知道它將到哪兒去,且知道在斜坡向上之前減速。
沿著當前方向,先走一步,然後再看向哪個方向走最快,這樣對前方的情況就有了更多地瞭解,可以做出明智的決策。
w_ahead = w - gama * v
# evaluate dw_ahead (the gradient at w_ahead instead of at w)
v = gama * v + learning_rate * dw_ahead
w -= vMomentum:
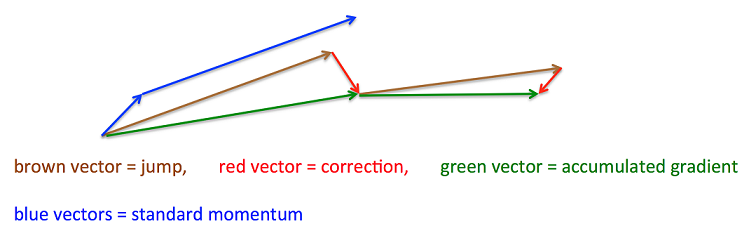
1)計算當前的梯度(上圖中:比較小的藍色向量)
2)沿著更新的累積的梯度方向進行一大跳(上圖中:比較大的藍色向量)
NAG:
1)沿著以前累積的梯度方向進行一大跳 (上圖中:棕色向量)
2)在新的位置測量梯度,然後進行校正(上圖中:綠色向量)
3)這個有預料的更新可以防止走的太快並導致增加的響應
關鍵區別:
1)計算梯度的位置不一樣
7.4 每個引數有自適應的學習率(Per-parameter Adaptive Learning Rate)
本章描述的方法(AdaGrad、AdaDelta、RMSprop、Adam)專為解決Learning Rate自適應的問題。
前面討論的基於梯度的優化方法(SGD、Momentum、NAG)的Learning Rate是全域性的,且對所有引數是相同的。
引數的有些維度變化快,有些維度變化慢;有些維度是負的斜坡,有些維度是正的斜坡(如鞍點);採用相同的Learning Rate是不科學的,比如有的引數可能已經到了僅需要微調的階段,但又有些引數由於對應樣本少等原因,還需要較大幅度的調動。理想的方案是根據引數每個維度的變化率,採用對應的Learning Rate。
下面討論如何自適應Learing Rate的方案:AdaGrad、AdaDelta、RMSProp、Adam。
7.4.1 AdaGrad(Adaptive Gradient )
關鍵優點:不需要手動調整Learning Rate,預設值為0.01即可。
關鍵缺點:在分母中累積了梯度的平方,且此累積值單調遞增,從而導致Learning Rate單調遞減,直至無限小,從而不能再學到相關知識(AdaDelta、RMSprop、Adam專為解決此問題而生)。
AdaGrad方法給引數的每個維度給出適應的Learning Rate。給不經常更新的引數以較大的Learning Rate, 給經常更新的引數以較小的Learning Rate。Google使用此優化方法“識別Youtube視訊中的貓” 。
在AdaGrad中,每個引數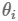
其公式如下:
其示意程式碼如下:
# Assume the gradient dx and parameter vector x
cache += dx**2
x -= learning_rate * dx / (np.sqrt(cache + 1e-8))learning_rate 是初始學習率,由於之後會自動調整學習率,所以初始值就不像之前的演算法那樣重要了。而1e-8指一個比較小的數,用來保證分母非0。
其含義是,對於每個引數,隨著其更新的總距離增多,其學習速率也隨之變慢。
7.4.2 AdaDelta (Adaptive Delta)
關鍵優點:1) 解決了AdaGrad Learning Rate單調遞減的問題。 (是AdaGrad的擴充套件)
2) 不需要設定預設的Learning Rate
RMS(Root Mean Squared) : 均方根
Adagrad演算法存在三個問題:
1)其學習率是單調遞減的,訓練後期學習率非常小
2)其需要手工設定一個全域性的初始學習率
3)更新W時,左右兩邊的單位不同
Adadelta針對上述三個問題提出了比較漂亮的解決方案。
7.4.3 RMSprop
RMSprop是由Geoff Hinton設計的。RMSprop與AdaDelta的目的一樣:解決AdaGrad的Learning Rate逐步消失的問題。
7.4.4 Adam (Adaptive Moment Estimation)
Adam的目的是:為每個引數計算自適應的Learning Rate。
其實際效果與AdaDelta、RMSProp相比,毫不遜色!
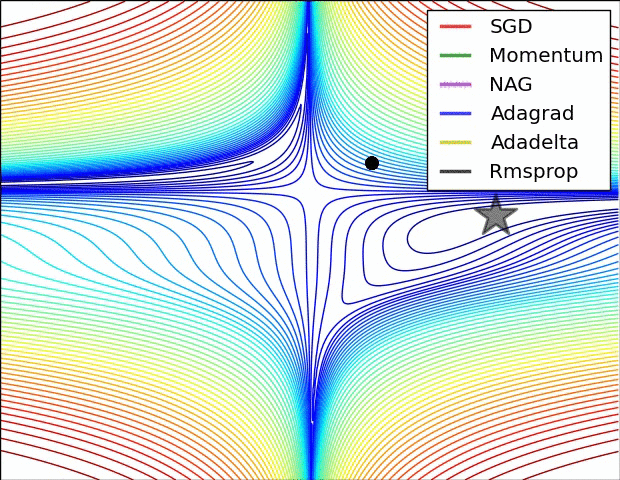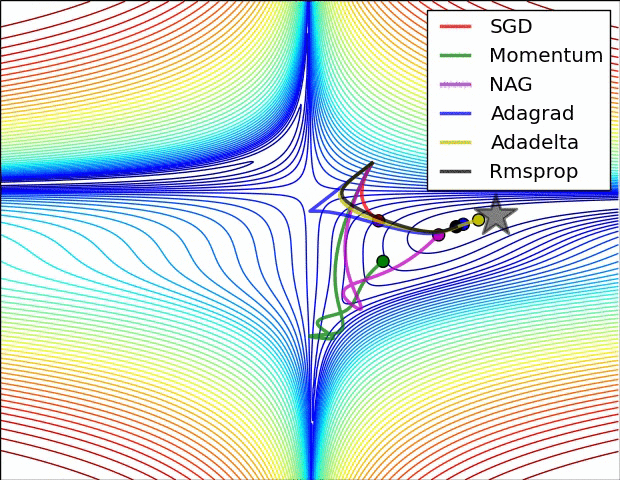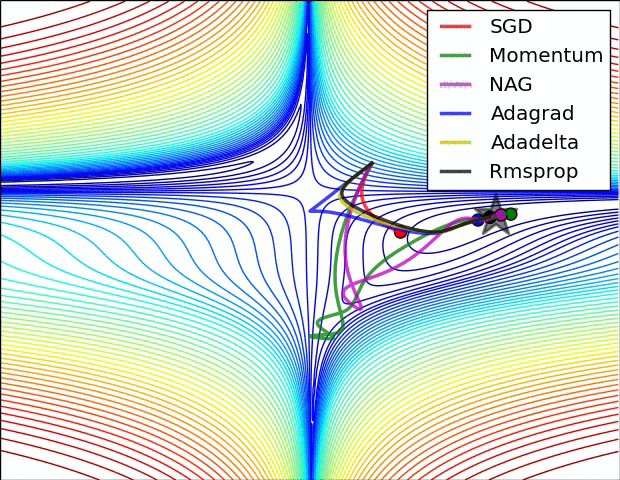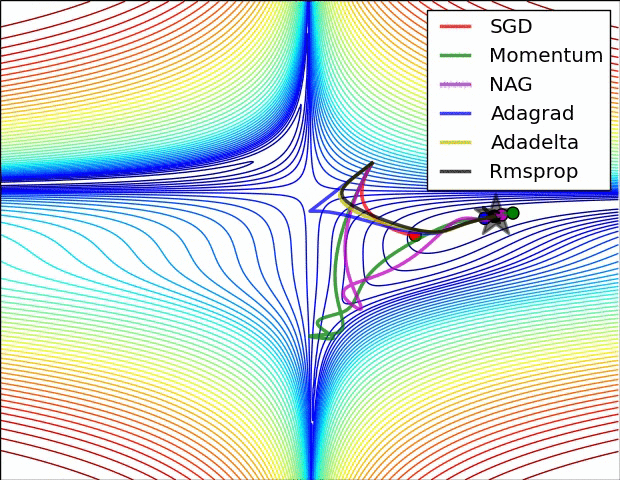
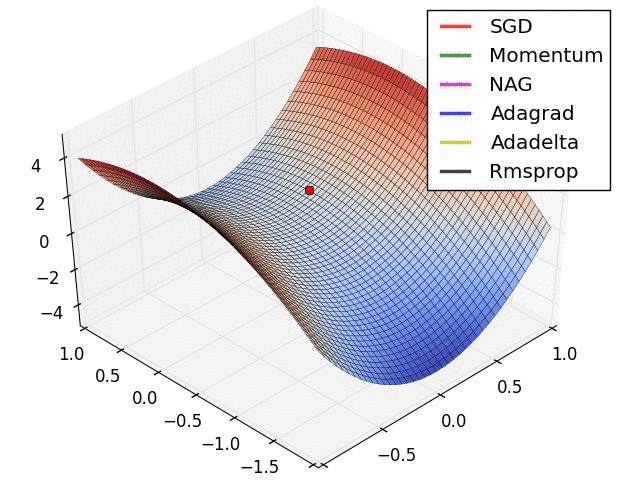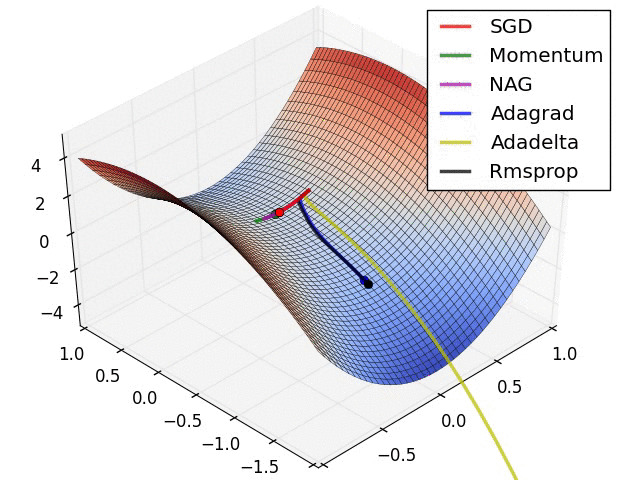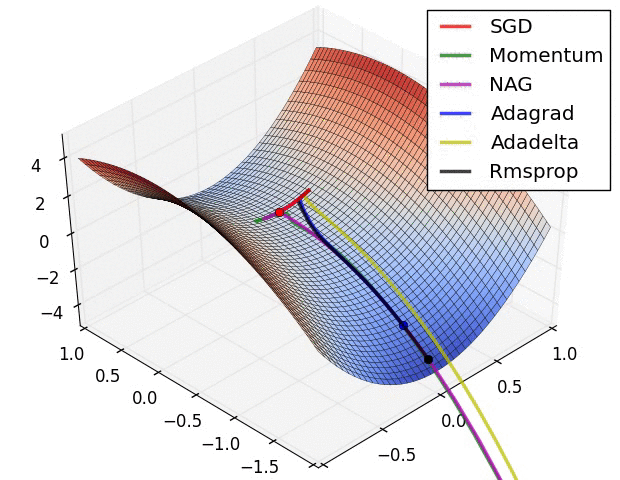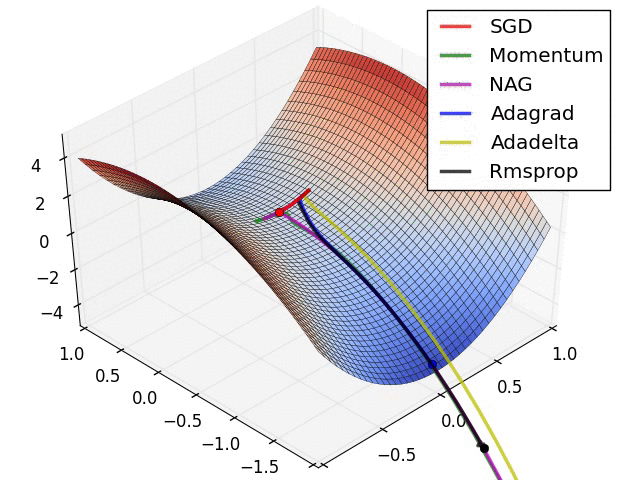
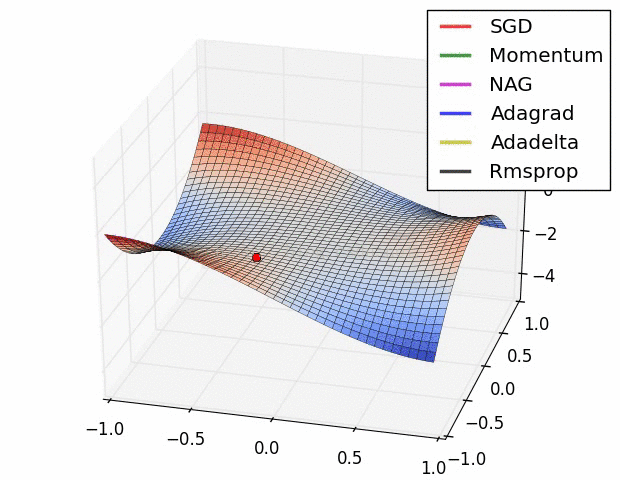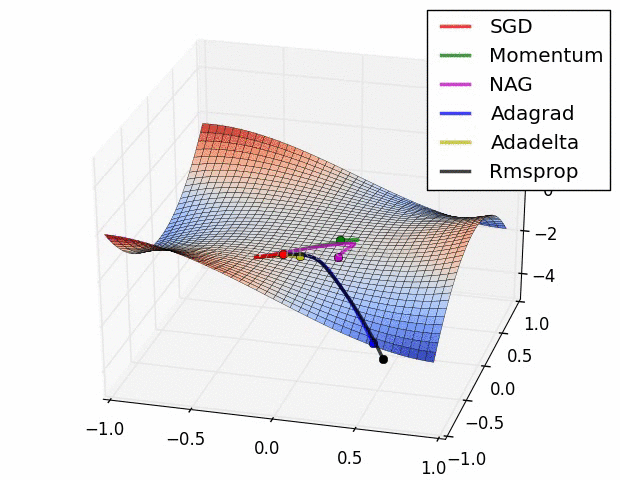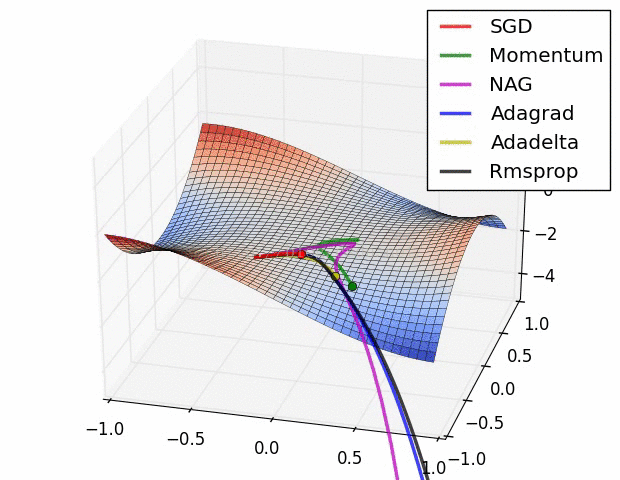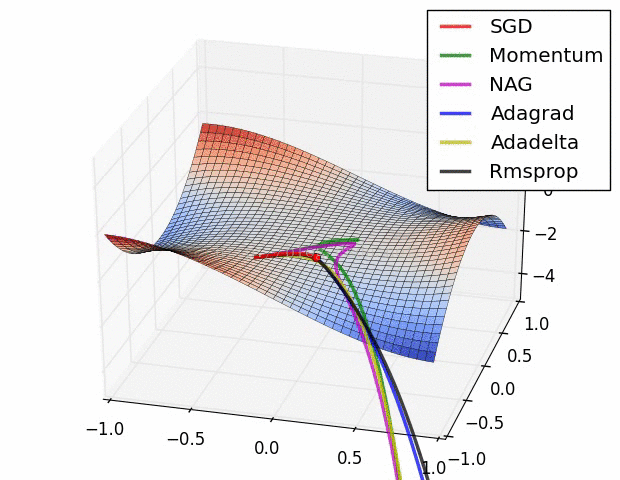
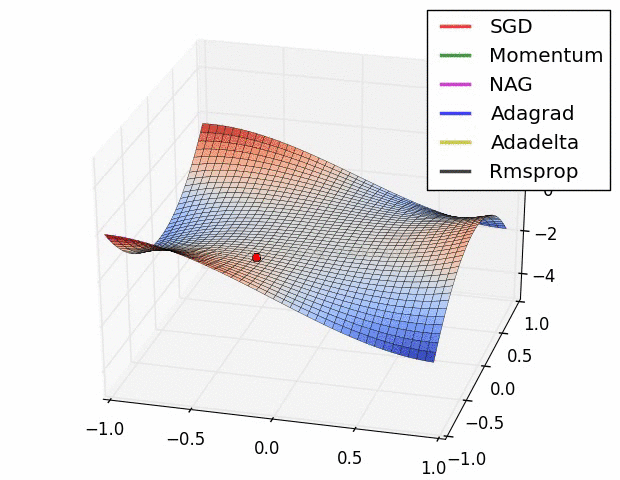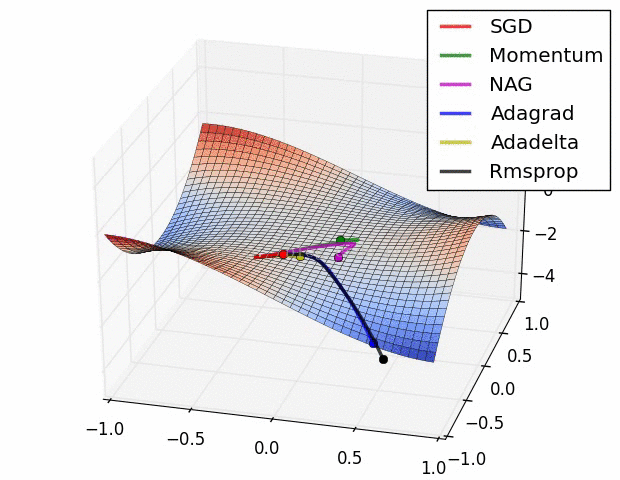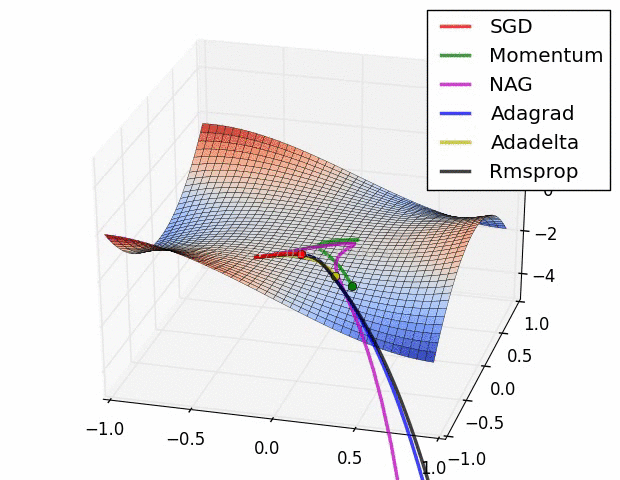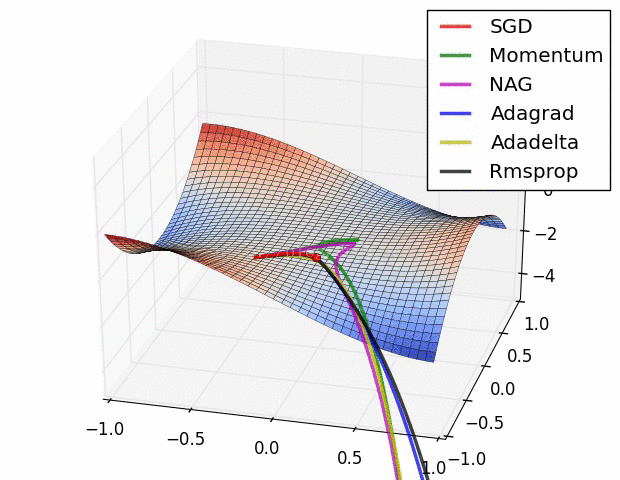
7.5 優化演算法效果視覺化
SGD optimization on Beale's function
SGD optimization on Long Valley
SGD optimization on Saddle Point
7.6 如何選擇優化演算法
1)總結:
- RMSprop是AdaGrad的擴充套件,以解決learning rate逐步消失的問題
- RMSprop與AdaDelta相比,AdaDelta在分子更新規則中使用了引數RMS更新,其它相同
- Adam與RMSprop相比,增加了偏差校正和動量
- RMSprop、AdaDelta和Adam是非常類似的演算法,在類似的環境下,效果相當
- 從整體上看,Adam目前是最好的選擇
2)如果輸入資料是稀疏的(sparse),使用adaptive learning-rate(AdaGrad、AdaDelta、RMSprop、Adam)可以獲得最好的結果,且不需要調整learning rate;
3)如果你關心快速收斂,你應當選擇adaptive learning-rate方法
7.7 優化SGD的其它策略
7.7.1 Shuffling and Curriculum Learning
1)Shuffling:每次迭代前,隨機打亂訓練樣本的順序
作用:增加隨機性。提高網路的泛化效能,避免因為有規律的資料出現,導致權重更新時的梯度過於極端,避免最終模型過擬合或欠擬合。
2)Curriculum Learning:把訓練樣本按某種有意義的方式進行排序,對逐步解決困難問題有效。
7.7.2 批量歸一化Batch Normalization (BN)
為了便於訓練,我們經常歸一化引數的初始值,通過mean=0, variance=1的高斯分佈來初始化引數。在訓練過程中,我們不同程度地更新引數,使用引數失去了歸一化,這將降低訓練速度且放大變化,網路越深問題越嚴重。
BN為每一個mini-batch重建歸一化引數。使模型結構的部分進行歸一化,我們可以使用更高的learning rate,且引數初始化要求沒哪麼高。
此外,BN還作為一個正則化(Regularizer),可以減少或避免使用Dropout。
正則化(Regularizer):是一個用於解決過擬合(Overfitting)問題的一種技術。具體實現方法是在損失函式中增加懲罰因子(引數向量的範數,1範數(L1)或2範數(L2))lambda*N(w)。
7.7.3 早期停止(Early Stopping)
在訓練時,總是監視驗證集的錯誤率,如果驗證集的錯誤率不能得到改善,應當停止訓練。
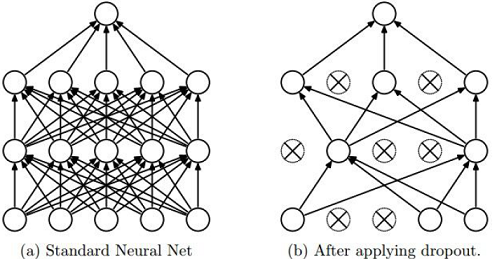
8. Regularization: Dropout
在前向計算時,隨機設定一些神經元的值為0,如下圖所示:
示意程式碼如下:
p = 0.5 # probability of keeping a unit active, higher = less dropout
def train_step(X)
""" X contains the data """
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
M1 = np.random.rand(*H1.shape) < p # first dropout mask
H1 *= M1 # drop
H2 = np.maximum(0, np.dot(W2, H1) + b2)
M2 = np.random.rand(*H2.shape) < p # send dropout mask
H2 *= M2 # drop
out = np.dot(W3,H2) + b3相當於訓練多個模型,一個dropout mask對應一個模型,且這些模型共享引數。
在測試時,不需要dropout, 直接計算每層的啟用值,然後進行scale作為本層最終輸出的啟用值,其程式碼如下:
def predict(X):
# ensembled forward pass
H1 = np.maxmium(0, np.dot(W1,X)+b1) * p # Note: scale the activations
H2 = np.maxmium(0, np.dot(W2,H1)+b2) * p # Note: scale the activations
out = np.dot(W3,H2) + b3