深度學習筆記2-啟用函式
深度學習筆記2-啟用函式
目前啟用函式有sigmoid、Tanh、ReLU、LeakyReLU、ELU。
-
Sigmoid函式
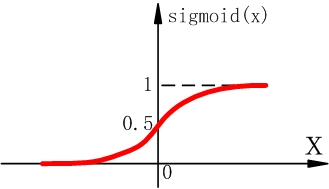
Sigmoid函式表示式 Sigmoid函式在遠離座標原點的時候,函式梯度非常小,在梯度反向傳播時,會造成梯度消失(梯度彌散),無法更新引數,即無法學習。另外,Sigmoid函式的輸出不是以零為中心的,這會導致後層的神經元的輸入是非0均值的訊號。那麼對於後層的神經元,其區域性梯度 永遠為正,假設更深層的神經元的梯度反向傳遞到這為 。根據鏈式法則,此時後層神經元的全域性梯度為 。當 為正時,對於所有的連線權 ,其都往“負”方向修正(因為 為正,要往負梯度方向修正);而當 為負時,對於所有的連線權 ,其都往“正”方向修正。所以,如果想讓 中的 往正方向修正的同時, 往負方向修正是做不到的。對於 會造成一種捆綁的效果,使得收斂很慢。如果是按batch來訓練的話,不同的batch會得到不同的符號,能緩和一下這個問題。
由於以上兩個缺點,sigmoid函式已經很少用了。 -
Tanh函式
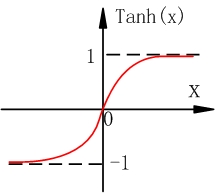
Tanh函式的表示式
Tanh函式能解決sigmoid函式輸出不是零均值的問題,但和sigmoid函式一樣,Tanh函式還是會存在很大的梯度彌散問題。 -
ReLU函式
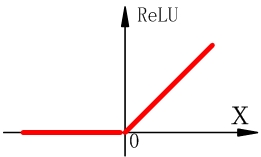
ReLU函式表示式為
ReLU函式在輸入為正的時候,不存在梯度彌散的問題,對梯度下降的收斂有巨大加速作用。同時由於它只是一個矩陣進行閾值計算,計算很簡單。但它也有兩個缺點,一個是當輸入x小於零時,梯度為零,ReLU神經元完全不會被啟用,導致相應引數永遠不會被更新;另一個和sigmoid一樣,輸出不是零均值的。 -
LeakyReLU函式
為了解決ReLU函式在輸入小於零神經元無法啟用的問題,人們提出了LeakyReLU函式。
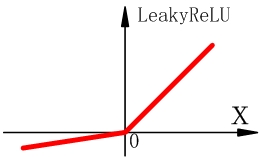
該函式在輸入小於零時,給了一個小的梯度(斜率,比如0.01)。因此就算初始化到輸入x小於零,也能夠被優化。其表示式為 , 為斜率。當把 作為引數訓練時,啟用函式就會變為PReLU。LeakyReLU以其優越的效能得到了廣泛的使用。 -
ELU函式
ELU函式也是ReLU函式的一個變形,也是為了解決輸入小於零神經元無法啟用的問題。
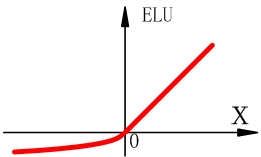
與LeakyReLU不同的是,當 時, 。
在tensorflow和pytorch中,都已經集成了這些啟用函式,可以拿來直接用。詳見:
http://www.tensorfly.cn/tfdoc/api_docs/python/nn.html#AUTOGENERATED-activation-functions
https://pytorch.org/docs/stable/nn.html#non-linear-activation-functions
