旅行商問題(Traveling Salesman Problem,TSP)的+Leapms線性規劃模型及c++呼叫
知識點
旅行商問題的線性規劃模型
旅行商問題的+Leapms模型及CPLEX求解
C++呼叫+Leapms
旅行商問題
旅行商問題是一個重要的NP-難問題。一個旅行商人目前在城市1,他必須對其餘n-1個城市訪問且僅訪問一次而後回到城市1,請規
劃其最短的迴圈路線。
旅行商問題的建模
設城市i,j之間的距離為D[i][j],又設0-1變數x[i][j]表示從城市i到城市j的道路是否在迴圈路線上。於是旅行商問題的目標可以被寫成:
min sum{i=1,...,n;j=1,...,n;i<>j}(D[i][j] x[i][j])
因每個城市必須被訪問一次且僅被訪問一次,於是對每個城市需要進入一次且僅一次,而且出去一次且僅一次,於是有以下兩個約束:
sum{i=1,...,n;i<>j} x[i][j] = 1 | j=2,...,n
sum{j=1,...,n;i<>j} x[i][j] = 1 | i=2,...,n
僅採用以上約束時,結果會形成多個不聯通的迴圈。為防止這種情況,為每個城市規定一個訪問循序的編號u[i]變數。u[i]=k表示該城市是第k個被訪問的城市。規定u[0]=1,任意u[i]<=n-1。顯然如果x[i][j]=1,即道路 i,j 被選定在迴圈路徑中,則u[j]>=u[i]+1。用以下約束表達這個邏輯:
u[j]>=u[i]+1-n(1-x[i][j])|i=1,...,n;j=2,...,n;i<>j
上式中,如果x[i][j]=1, 則等價於u[j]>=u[i]+1。如果x[i][j]=0,則右端小於等於0,恆小於等於左端,相當於該約束不存在。
旅行商問題的Leapms模型
使用Cd表示城市的地理座標,則問題的Leapms模型為
//The Traveling Salesman Problem
min sum{i=1,...,n;j=1,...,n;i<>j} x[i][j] D[i][j]
subject to
sum{i=1,...,n;i<>j} x[i][j] = 1 | j=2,...,n
sum{j=1,...,n;i<>j} x[i][j] = 1 | i=2,...,n
u[1]=0
u[j]>=u[i]+1-n(1-x[i][j])|i=1,...,n;j=2,...,n;i<>j
u[i]<=n-1|i=1,...,n
where
n is an integer
Cd is a set
D[i][j] is a number|i=1,...,n;j=1,...,n
x[i][j] is a variable of binary|i=1,...,n;j=1,...,n;i<>j
u[i] is a variable of nonnegative number|i=1,...,n
data_relation
n=_$(Cd)/2
D[i][j]=sqrt((Cd[2i-1]-Cd[2j-1])^2+(Cd[2i]-Cd[2j])^2) -->
|i=1,...,n;j=1,...,n
data
Cd={
0 0
1062 182
1028 503
206 200
473 291
1741 233
}//六個城市使用mip或者cplex命令瞬間可以求解上述模型
Welcome to +Leapms ver 1.1(162260) Teaching Version -- an LP/LMIP modeling and
solving tool.歡迎使用利珀 版本1.1(162260) Teaching Version -- LP/LMIP 建模和求
解工具.
+Leapms>load
Current directory is "ROOT".
.........
current.leap
tsp.leap
tsp_tamplet.leap
.........
please input the filename:tsp
================================================================
1: //The Traveling Salesman Problem
2: min sum{i=1,...,n;j=1,...,n;i<>j} x[i][j] D[i][j]
3: subject to
4: sum{i=1,...,n;i<>j} x[i][j] = 1 | j=2,...,n
5: sum{j=1,...,n;i<>j} x[i][j] = 1 | i=2,...,n
6:
7: u[1]=0
8: u[j]>=u[i]+1-n(1-x[i][j])|i=1,...,n;j=2,...,n;i<>j
9: u[i]<=n-1|i=1,...,n
10: where
11: n is an integer
12: Cd is a set
13: D[i][j] is a number|i=1,...,n;j=1,...,n
14: x[i][j] is a variable of binary|i=1,...,n;j=1,...,n;i<>j
15: u[i] is a variable of nonnegative number|i=1,...,n
16: data_relation
17: n=_$(Cd)/2
18: D[i][j]=sqrt((Cd[2i-1]-Cd[2j-1])^2+(Cd[2i]-Cd[2j])^2) -->
19: |i=1,...,n;j=1,...,n
20: data
21: Cd={
22: 0 0
23: 1062 182
24: 1028 503
25: 206 200
26: 473 291
27: 1741 233
28: 1815 633
29: 1060 916
30: }//八個城市
31:
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=64
number of constraints=72
..................................
+Leapms>mip
relexed_solution=3006.07; number_of_nodes_branched=0; memindex=(2,2)
nbnode=138; memindex=(26,26) zstar=4880.76; GB->zi=4802.4
nbnode=337; memindex=(24,24) zstar=4328.8; GB->zi=4802.4
nbnode=513; memindex=(12,12) zstar=4112.39; GB->zi=4549.03
nbnode=697; memindex=(16,16) zstar=4541.65; GB->zi=4549.03
The Problem is solved to optimal as an MIP.
找到整數規劃的最優解.非零變數值和最優目標值如下:
.........
u2* =1
u3* =5
u4* =7
u5* =6
u6* =2
u7* =3
u8* =4
x1_2* =1
x2_6* =1
x3_5* =1
x4_1* =1
x5_4* =1
x6_7* =1
x7_8* =1
x8_3* =1
.........
Objective*=4549.03
.........
+Leapms>
C++呼叫+Leapms模型
直接的+leapms求解得到的是變數的結果資料,如果要進一步處理,則使用高階語言呼叫則更加方便。
+Leapms提供了c_leap類可以做此工作。主要的函式是:
c_leap::loadleap(char *leapfile) -- 調入名為leapfile的leapms模型
c_leap::mip() -- 求解當前的leapms模型(使用leapms自帶求解器,功能較弱)
c_leap::cplex() -- 求解當前的leapms模型(使用CPLEX求解器)
c_leap::getObj() -- 返回當前最優解的目標值
c_leap::getVar(char *varname) -- 返回變數名為varname的值
c_leap::getVar(char *varname,int nid, int id1,...) -- 返回變數名為varname,腳標個數為nid, 腳標分別為id1,...的變數的值。
把城市座標資料放在loc.txt中,下面的c++程式碼可以根據leapms模型模板(即去掉data段的旅行商問題leapms模型)生成當前模型、求解當前模型,並輸出autocad批處理圖形指令碼。
#include<iostream>
#include<fstream>
#include "leap.h"
using namespace std;
int m;
double x[3000],y[3000];
//例項化leap物件
c_leap lp;
//讀原始資料生成當前模型
bool genModel(string fmodel,string fdata){
ifstream iff;
ofstream off;
//複製模板到當前模型current.leap中
iff.open(fmodel);
off.open("current.leap");
if(!iff||!off)return false;
string line;
while(getline(iff,line)){
off<<line<<endl;
}
iff.close();
//讀入資料檔案新增到當前模型的資料區
iff.open(fdata);
if(!iff)return false;
off<<"data"<<endl<<"\tCd={"<<endl;
int i=0;
while(!iff.eof()){
iff>>x[i]>>y[i];
off<<"\t\t"<<x[i]<<" "<<y[i]<<endl;
i++;
}
m=i;
off<<"\t}"<<endl;
iff.close();
off.close();
//結束模型生成過程
return true;
}
//輸出圖形
void draw(){
ofstream ocad;
ocad.open("tsp.scr");
if(!ocad){
cout<<"\t輸出圖形錯誤!"<<endl;
return;
}
for(int i=0;i<m;i++){
ocad<<"color 7"<<endl;
ocad<<"point "<<x[i]<<","<<y[i]<<endl;
for(int j=0;j<m;j++){
if(i==j)continue;
if(lp.getVar("x",2,i+1,j+1)>0){
ocad<<"color 1"<<endl;
ocad<<"line "<<x[i]<<","<<y[i]<<" "<<x[j]<<","<<y[j]<<" "<<endl;
}
}
}
ocad.close();
}
int main(){
//讀原始資料生成當前模型
if(!genModel("tsp_tamplet.leap","loc.txt")){
cout<<"\t錯誤!不能開啟檔案!"<<endl;
return -1;
}
//調入模型
lp.loadLeap("current.leap");
//使用cplex求解模型的整數解
lp.cplex();
//輸出旅行商路徑圖形
draw();
//結束程式
return 0;
}
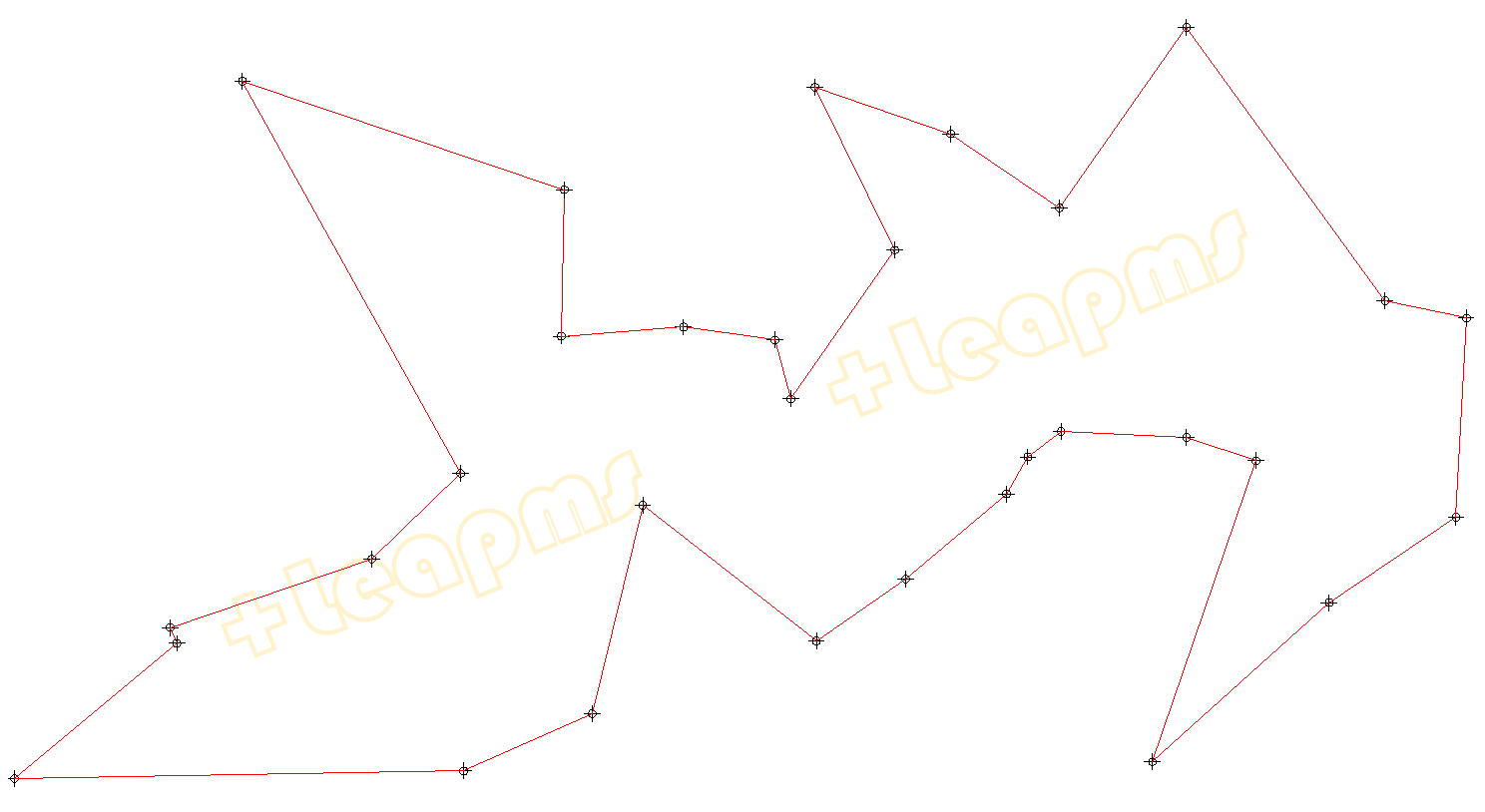
對31個城市TSP問題的求解結果:
城市分佈

巡迴路線