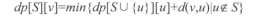動態規劃的狀態有時不易表示，需要用一些編碼技術把狀態用簡單的方式表示。一般資料n<16或者n<32很可能就是狀態壓縮dp法的標誌，要注意好這些資料規模的提示作用。我們以TSP問題為例用狀態壓縮dp法解決。TSP問題(Traveling Salesman Problem)是數學領域中著名問題之一。假設有一個旅行商人要拜訪N個城市，他必須選擇所要走的路徑，路徑的限制是每個城市只能拜訪一次，而且最後要回到原來出發的城市，要求路徑的總和最小。其中，N<=16。
我們先考慮如何表示一個點集。由於只有16個點，所以我們用一個整數表示一個點集。例如5=0000 0000 0000 0101，它的第0位和第2位是1，就表示這個點集裡有2個點，分別是點0和點2。

dp[S][v]中S表示已經訪問過的頂點集合不包括起點0，v表示當前所在的頂點陣列的值，dp[S][v]的值表示從v出發訪問剩餘的所有頂點最終回到頂點0的路徑的權重總和的最小值。這樣，dp[0][0]即為所求解。初始化時，除了dp[(1<<n)-1][0]=0之外，其餘的值都是INF。狀態轉移方程如下。

狀態壓縮DP

DP過程中的狀態不可能像揹包問題一樣只有整數，肯定有各種各樣稀奇古怪的狀態，需要不止一個變數來表示。這種情況下如果需要使用DP 就必須把狀態壓縮成一個數來表示，並且一個數只能對應於一種狀態。

特別地，對於集合我們可以把每一個元素的選取與否對應到一個二進位制位裡，從而把狀態壓縮成一個整數，大大方便了計算和維護。

對於不是整數的情況，很多時候很難確定一個合適的遞推順序，因此使用記憶化搜尋可以避免這個問題。如下面TSP問題的法一。

TSP問題

一張圖上有n個點，給定相應的鄰接矩陣，需要求出從0號節點出發，經過且只經過每個頂點一次，最後仍回到0號節點的最小邊權。TSP問題可以用狀壓DP來快速求解。

定義dp[S][v]為已經經過了點集S之後，目前在點v(v已經包含在S中)，回到0節點的最小邊權。 
所以有如下的遞推公式

**dp[V[0] = 0 
dp[S][v] = min(dp[S∪{u}][u]+d[v][u])(其中u不屬於S)**

將S看作一個長度為n的bit流，第幾號節點訪問過就把S的第幾號節點置為1，其他都是0，這樣就可以將狀態壓縮成了一個數字來表示，並且有一一對應性。

採用記憶化搜尋的TSP狀壓DP程式碼如下

int n;
int d[maxn][maxn];
int dp[1<<maxn][maxn];
int rec(int S,int v)
{
    if(dp[S][v] >= 0) {
        return dp[S][v];
    }
    if(v == 0 && S == (1<<maxn)-1) return dp[S][v] = 0;
    int ans = INF;
    for(int i = 0 ; i < n ; i ++) {
        if(!(S>>i&1)) {
            ans = min(ans,d[v][i]+rec(S|(1<<i),i));
        }
    }
    return dp[S][v] = ans;
}
void solve(void)
{
    memset(dp,-1,sizoef(dp));
    cout << rec(0,0) << endl;
}

此外也可以不用記憶化搜尋，觀察遞推的順序從而使用迴圈求解。 

發現對於任意的兩個整數i和j 如果它們對應的集合滿足S(i)包含於S(j) 那麼i<=j。

程式碼如下

int dp[1<<maxn][maxn];
void solve()
{
    for(int i = 0 ; i < (1<<n) ; i ++) {
        fill(dp[S],dp[S]+n,INF);
    }
    dp[(1<<n)-1][0] = 0;
    for(int S = (1<<n)-1 ; S >= 0 ; S --) {
        for(int i = 0 ; i < n ; i ++) {
            for(int j = 0 ; j < n ; j ++) {
                if(!(S>>j&1))
                    dp[S][i] = min(dp[S][i],dp[S|1<<j][j]+d[i][j]);
            }
        }
    }
    cout << dp[0][0] << endl;
}

HDU 5067的狀壓dp程式碼

#include <iostream>
#include <stdio.h>
#include <cmath>
#include <cstring>
#include <algorithm>

using namespace std;

#define ll long long
#define LL long long
#define inf 0x3f3f3f3f

int a[150][150];
int dp[(1<<11)][20];
int xx[20],yy[20];

int cnt;

int dfs(int num,int now)
{
    if(dp[num][now]!=-1) return dp[num][now];
    int t=num;
    int ret=inf;
    for(int i=0;i<cnt;i++)
    {
        if(!((num>>i)&1))
        {
            int t=num+(1<<i);
            int ans=dfs(t,i)+abs(xx[i]-xx[now])+abs(yy[i]-yy[now]);
            ret=min(ans,ret);
        }
    }
    if(ret==inf)return dp[num][now]=xx[now]+yy[now];
    return dp[num][now]=ret;
}

int main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        memset(a,0,sizeof(a));
        cnt=0;
        xx[0]=yy[0]=0;
        cnt++;
        memset(dp,-1,sizeof(dp));
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            {
                int t;
                scanf("%d",&t);
                if(t)
                {
                    xx[cnt]=i,yy[cnt]=j;
                    a[i][j]=cnt++;
                }
            }
            printf("%d\n",dfs(1,0));
    }
    return 0;
}

#include <iostream>
#include <stdio.h>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <stack>
#define inf 0x3f3f3f3f

using namespace std;

typedef long long ll;

int p[15][2];
int ans,cnt;
int vis[15];
void dfs(int x, int y,int now,int dis)
{
    if(dis>=ans)
        return ;
    if(now==cnt)
    {
        ans=min(ans,dis+x+y);
        return ;
    }

    for(int i=0;i<cnt;i++)
    {
        if(vis[i]==0)
        {
            vis[i]=1;
            int dist=dis+abs(x-p[i][0])+abs(y-p[i][1]);
            dfs(p[i][0],p[i][1],now+1,dist);
            vis[i]=0;
        }
    }

}

int main()
{
    int n,m,tmp;
    while(~scanf("%d%d",&n,&m))
    {
        cnt=0;
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                scanf("%d",&tmp);
                if(i==0&&j==0)
                    continue;
                if(tmp!=0)
                {
                    p[cnt][0]=i;
                    p[cnt++][1]=j;
                }
            }
        }
        memset(vis,0,sizeof(vis));
        ans=10000000;
        dfs(0,0,0,0);
        printf("%d\n",ans);
    }
    return 0;
}