本文內容來自於論文：Tag recommendations based on tensor dimensioanlity reduction

在社會標籤系統中，存在三元關係，使用者-物品-標籤。這些資料最直觀的表示方式是三維陣列（張量）。

論文小例子的設定如下圖，

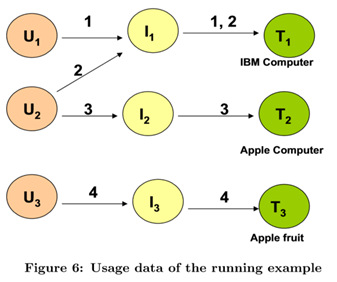
使用者1 對 物品1 打的標籤是 T1(IBM 電腦),

使用者2對 物品1 打的標籤是 T1(IBM 電腦)

其他類似，不贅述。

設定標註過的對應位置為1，沒標註的為0。則上圖的資料可以表示成一個三階稀疏張量(sparse tensor)。 

使用tucker分解中的一個特殊情形HOSVD（tucker分解和HOSVD 不同在於 HOSVD 要求 因子矩陣是 正交的）

關於HOSVD，可以直接看Tensor Decomposition and Application 這篇論文。（這是關於張量分解的 綜述論文，非常經典）

MATLAB  tensor toolbox 實現

%%%Paper: Tag Recommendations based on Tensor Dimensionality Reduction 

A = zeros([3 3 3]);
A(1,1,1)=1;
A(2,1,1)=1;
A(2,2,2)=1;
A(3,3,3)=1;

A = tensor(A);

% tucker decomposition
result = tucker_als(A,[2,3,3]);

% tensor recovery
A_hat = ttm( result.core ,{ result.U{1} , result.U{2} , result.U{3} });
disp(A_hat);
 

tucker_als（）方程能對稀疏張量分解，引數[2 3 3],意思是認為 在人這個維度上秩為2，就是說有3個人，但只有2種人。其他維度都是滿秩的。當然，你也可以自行設定各個維度的引數。

再使用張量的n-模乘 ttm() ，恢復張量$ \hat{A} $。結果如下:

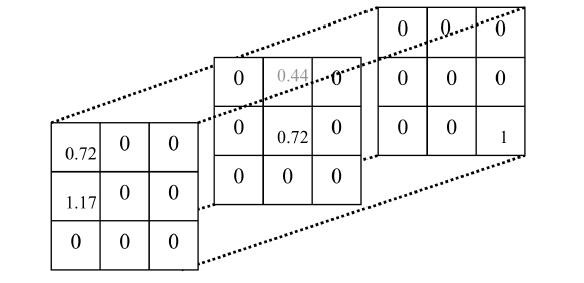
在標籤2下使用者1對物品2的正反饋為0.44。 說明在這個標籤2 (Apple Computer)下，該給他推薦商品2。

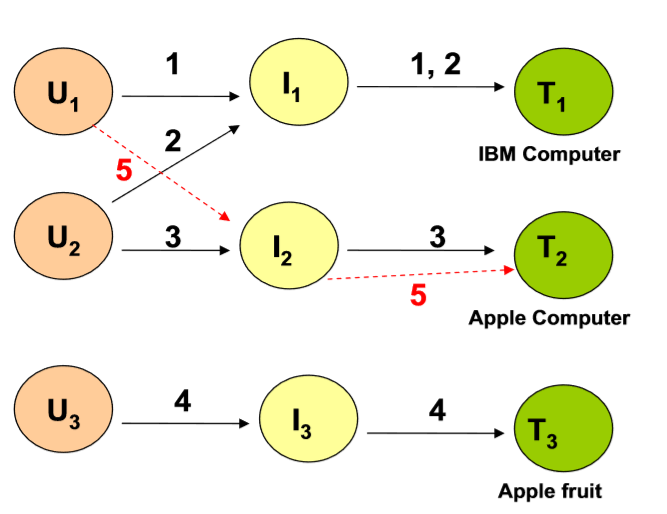
張量恢復可以用來進行多模式推薦，例如向用戶推薦物品，向用戶推薦標籤...

從使用者-物品的角度看，通過HOSVD我們向喜歡IBM電腦的使用者推薦了Apple 電腦。

本文張量圖形來自於: https://blog.csdn.net/zd836614437/article/details/51601720