轉載：http://www.cnblogs.com/skywang12345/

迪傑斯特拉演算法介紹

迪傑斯特拉(Dijkstra)演算法是典型最短路徑演算法，用於計算一個節點到其他節點的最短路徑。 
它的主要特點是以起始點為中心向外層層擴充套件(廣度優先搜尋思想)，直到擴充套件到終點為止。

基本思想

     通過Dijkstra計算圖G中的最短路徑時，需要指定起點s(即從頂點s開始計算)。

     此外，引進兩個集合S和U。S的作用是記錄已求出最短路徑的頂點(以及相應的最短路徑長度)，而U則是記錄還未求出最短路徑的頂點(以及該頂點到起點s的距離)。

     初始時，S中只有起點s；U中是除s之外的頂點，並且U中頂點的路徑是"起點s到該頂點的路徑"。然後，從U中找出路徑最短的頂點，並將其加入到S中；接著，更新U中的頂點和頂點對應的路徑。 然後，再從U中找出路徑最短的頂點，並將其加入到S中；接著，更新U中的頂點和頂點對應的路徑。 ... 重複該操作，直到遍歷完所有頂點。

操作步驟

(1) 初始時，S只包含起點s；U包含除s外的其他頂點，且U中頂點的距離為"起點s到該頂點的距離"[例如，U中頂點v的距離為(s,v)的長度，然後s和v不相鄰，則v的距離為∞]。

(2) 從U中選出"距離最短的頂點k"，並將頂點k加入到S中；同時，從U中移除頂點k。

(3) 更新U中各個頂點到起點s的距離。之所以更新U中頂點的距離，是由於上一步中確定了k是求出最短路徑的頂點，從而可以利用k來更新其它頂點的距離；例如，(s,v)的距離可能大於(s,k)+(k,v)的距離。

(4) 重複步驟(2)和(3)，直到遍歷完所有頂點。

單純的看上面的理論可能比較難以理解，下面通過例項來對該演算法進行說明。

迪傑斯特拉演算法圖解

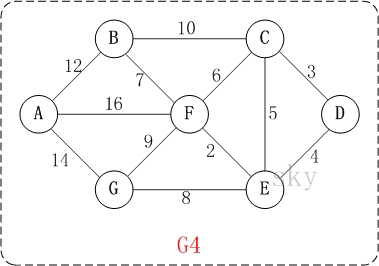
以上圖G4為例，來對迪傑斯特拉進行演算法演示(以第4個頂點D為起點)。

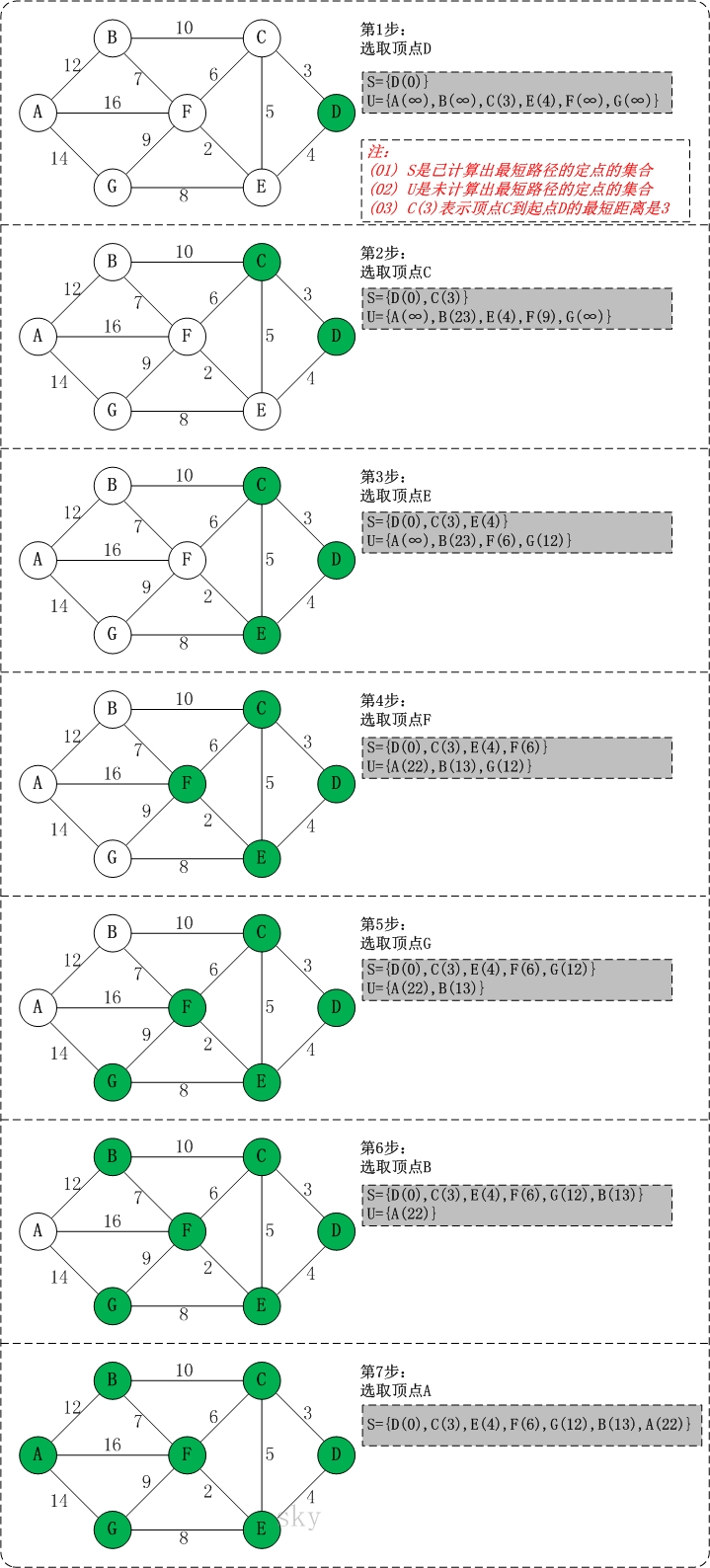
初始狀態：S是已計算出最短路徑的頂點集合，U是未計算除最短路徑的頂點的集合！ 
第1步

第2步：將頂點C加入到S中。 
    上一步操作之後，U中頂點C到起點D的距離最短；因此，將C加入到S中，同時更新U中頂點的距離。以頂點F為例，之前F到D的距離為∞；但是將C加入到S之後，F到D的距離為9=(F,C)+(C,D)。 
    此時，S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。

第3步：將頂點E加入到S中。 
    上一步操作之後，U中頂點E到起點D的距離最短；因此，將E加入到S中，同時更新U中頂點的距離。還是以頂點F為例，之前F到D的距離為9；但是將E加入到S之後，F到D的距離為6=(F,E)+(E,D)。 
    此時，S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。

第4步：將頂點F加入到S中。 
    此時，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：將頂點G加入到S中。 
    此時，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：將頂點B加入到S中。 
    此時，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：將頂點A加入到S中。 
    此時，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此時，起點D到各個頂點的最短距離就計算出來了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

迪傑斯特拉演算法的程式碼說明

以"鄰接矩陣"為例對迪傑斯特拉演算法進行說明，對於"鄰接表"實現的圖在後面會給出相應的原始碼。

1. 基本定義

public class MatrixUDG {

    private int mEdgNum;        // 邊的數量
    private char[] mVexs;       // 頂點集合
    private int[][] mMatrix;    // 鄰接矩陣
    private static final int INF = Integer.MAX_VALUE;   // 最大值

    ...
}

MatrixUDG是鄰接矩陣對應的結構體。mVexs用於儲存頂點，mEdgNum用於儲存邊數，mMatrix則是用於儲存矩陣資訊的二維陣列。例如，mMatrix[i][j]=1，則表示"頂點i(即mVexs[i])"和"頂點j(即mVexs[j])"是鄰接點；mMatrix[i][j]=0，則表示它們不是鄰接點。

2. 迪傑斯特拉演算法

/*
 * Dijkstra最短路徑。
 * 即，統計圖中"頂點vs"到其它各個頂點的最短路徑。
 *
 * 引數說明：
 *       vs -- 起始頂點(start vertex)。即計算"頂點vs"到其它頂點的最短路徑。
 *     prev -- 前驅頂點陣列。即，prev[i]的值是"頂點vs"到"頂點i"的最短路徑所經歷的全部頂點中，位於"頂點i"之前的那個頂點。
 *     dist -- 長度陣列。即，dist[i]是"頂點vs"到"頂點i"的最短路徑的長度。
 */
public void dijkstra(int vs, int[] prev, int[] dist) {
    // flag[i]=true表示"頂點vs"到"頂點i"的最短路徑已成功獲取
    boolean[] flag = new boolean[mVexs.length];

    // 初始化
    for (int i = 0; i < mVexs.length; i++) {
        flag[i] = false;          // 頂點i的最短路徑還沒獲取到。
        prev[i] = 0;              // 頂點i的前驅頂點為0。
        dist[i] = mMatrix[vs][i];  // 頂點i的最短路徑為"頂點vs"到"頂點i"的權。
    }

    // 對"頂點vs"自身進行初始化
    flag[vs] = true;
    dist[vs] = 0;

    // 遍歷mVexs.length-1次；每次找出一個頂點的最短路徑。
    int k=0;
    for (int i = 1; i < mVexs.length; i++) {
        // 尋找當前最小的路徑；
        // 即，在未獲取最短路徑的頂點中，找到離vs最近的頂點(k)。
        int min = INF;
        for (int j = 0; j < mVexs.length; j++) {
            if (flag[j]==false && dist[j]<min) {
                min = dist[j];
                k = j;
            }
        }
        // 標記"頂點k"為已經獲取到最短路徑
        flag[k] = true;

        // 修正當前最短路徑和前驅頂點
        // 即，當已經"頂點k的最短路徑"之後，更新"未獲取最短路徑的頂點的最短路徑和前驅頂點"。
        for (int j = 0; j < mVexs.length; j++) {
            int tmp = (mMatrix[k][j]==INF ? INF : (min + mMatrix[k][j]));
            if (flag[j]==false && (tmp<dist[j]) ) {
                dist[j] = tmp;
                prev[j] = k;
            }
        }
    }

    // 列印dijkstra最短路徑的結果
    System.out.printf("dijkstra(%c): \n", mVexs[vs]);
    for (int i=0; i < mVexs.length; i++)
        System.out.printf("  shortest(%c, %c)=%d\n", mVexs[vs], mVexs[i], dist[i]);
}

傑斯特拉演算法的原始碼

這裡分別給出"鄰接矩陣圖"和"鄰接表圖"的迪傑斯特拉演算法原始碼。

1. 鄰接矩陣原始碼(MatrixUDG.java)

2. 鄰接表原始碼(ListUDG.java)