通過前面的知識，我們已經知道，有序的資料在查詢時有極大的效能提升。很多查詢都基於有序資料，但並不是所有的結構都能像二叉排序樹一樣，在插入資料時就已經排好序，很多時候往往是無序的資料，需要我們使用時再進行排序，這就意味著我們需要尋找高效率的排序演算法。接下來，我們對當下使用較為普遍的幾個演算法逐一進行分析。這裡推薦一個可以檢視演算法執行動態過程的網站，加深對演算法原理的理解。

基礎知識 排序定義 假設含有n個記錄的序列為{r1. r2, ..., rn}，其相應的關鍵字分別為{k1, k2, ..., kn}，需確定1, 2, ..., n的一種排列p1, p2, ..., pn，使其相應的關鍵字滿足kp1≤kp2≤...≤kpn(非遞減或非遞增) 關係，即使得序列成為一個按關鍵字有序的序列{rp1, rp2, ..., rpn} ， 這樣的操作就稱為排序。

穩定性 假設ki=kj( 1≤i≤n, 1≤j≤ n, i≠j ) ，且在排序前的序列中 ri 領先於 rj (即i<j) 。如果排序後 ri 仍領先於 rj，則稱所用的排序方法是穩定的；反之，若可能使得排序後的序列中 rj 領先 ri，則稱所用的排序方法是不穩定的。

簡單來說，就是對於原資料中相等的資料，排序前後如果相對位置沒有改變，就是穩定的。

內排序與外排序 內排序是在排序整個過程中，待排序的所有記錄全部被放置在記憶體中。外排序是由於排序的記錄個數太多，不能同時放置在記憶體，整個排序過程需要在內外存之間多次交換資料才能進行。本文先介紹內排序演算法，外排序以後再來分析。

氣泡排序 氣泡排序（Bubble Sort）是一種交換排序，它的基本思想是：兩兩比較相鄰記錄的關鍵字，如果反序則交換，直到沒有反序的記錄為止。

氣泡排序可能是我們最熟悉的排序演算法了，它的核心在於兩兩交換，程式碼程式碼：

private void bubbleSort(int[] arr){ int len = arr.length;

for (int i = 0; i < len-1; i++) {
    for (int j=0; j < len-1-i; j++) {
        if(arr[j]>arr[j+1]){
            swap(arr, j, j+1);
        }
    }
}

} 它的最壞時間複雜度是1+2+...+(n-1) = n(n-1)/2，也就是O(n2)，這個複雜度相對還是比較高的，所以只適合小量資料排序。因為氣泡排序每次遍歷後，最後的資料一定是有序的，所以當初始資料部分有序時，還可以對它進行優化。比如陣列為{1,0,5,6,7,8,9,10}，當第一次遍歷後，陣列就是有序的，這時後續的迴圈遍歷都是沒有用的，優化後的演算法如下：

private void bubbleSort1(int[] arr){ int len = arr.length; boolean flag = false; for (int i = 0; i < len-1; i++) { flag = false; for (int j=0; j < len-1-i; j++) { if(arr[j]>arr[j+1]){ swap(arr, j, j+1); flag = true; } } } } 使用一個flag標記是否有資料交換，氣泡排序如果沒有資料交換，則意味著後邊的資料一定是有序的，這樣一來可以有效地提高氣泡排序的效能。但總體而言，氣泡排序還是不適合大資料量、資料比較亂的情況。

簡單選擇排序 選擇排序的思想是每一趟從待排序的記錄中選出最小的元素，順序放在已排好序的序列最後，直到全部記錄排序完畢。簡單選擇排序就基於此思想，除此之外還有樹型選擇排序和堆排序也是基於此思想。

簡單選擇排序法就是通過n-i次關鍵字間的比較，從n-i+1個記錄中選出關鍵字最小的記錄，並和第 i (0≤i≤n)個記錄交換。

它的實現如下：

private void selectSort(int[] arr){ int len = arr.length; int min; for (int i = 0; i < len; i++) { min = i; for (int j = i+1; j < len; j++) { if(arr[min]>arr[j]){ min = j; } } if(i!=min){ swap(arr,i,min); } } } 總體來看，簡單排序演算法的最壞時間複雜度也是O(n2)，但是它交換資料的次數明顯比氣泡排序要少很多，所以效能也比氣泡排序略優。

直接插入排序 直接插入排序和我們排序撲克牌的道理一致，就是把新的一張牌插入到已經排好序的牌中，它的基本操作是將一個記錄插入到已經排好序的有序表中，從而得到一個新的、記錄數增1的有序表。它的程式碼實現如下：

private void insertSort(int[] arr){ int len = arr.length; int temp; for (int i = 0; i < len; i++) { for (int j = 0; j < i; j++) { if(arr[i]<arr[j]){ temp = arr[i]; // j及以後的記錄向後移動一位，然後把當前值存放在j的位置 System.arraycopy(arr,j,arr,j+1,i-j); arr[j] = temp; } } } } 它的最壞時間複雜度依然是O(n2)。

我們介紹了三種最簡單，最容易理解的演算法，但是它們的效率也確實較低。在資料量小的時候影響不大，然而現實是我們更多地要對大量資料進行排序。接下來介紹的幾種演算法屬於改進演算法，它們的效率都較為高一些。

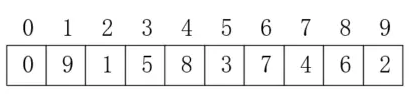
希爾排序 簡單的排序演算法，都需要在資料量少，或者部分有序的情況下，才能發揮較好的效能。但是再大規模的資料都可以拆分成多個小規模的資料，希爾排序的思想就是把大規模的資料拆分成多個小規模資料，然後每部分分別進行直接插入排序，最後再對全部資料進行整體排序。如何拆分就是希爾排序的重點，比如資料是{0, 9, 2, 4, 6, 1}，要將它拆成兩部分，如果按照前後拆分，那麼進行直接插入排序後結果是{0, 2, 9, 1, 4, 6}，這樣排序後對後續整體排序沒有幫助。那麼希爾排序是如何做的呢？我們先通過一個簡單的陣列來演示希爾排序的過程，首先有陣列如下： 希爾排序 假設第一次取資料的一半作為間隔值，之後每次減半，我們把這個值記為inc，那麼第一次inc=5，我們在對應位置前加一條紅色虛線表示，如下所示：

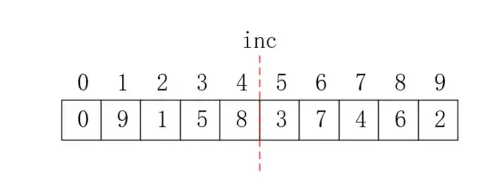
接下來我們就要進行直接插入排序了，前面說過希爾排序不是按照前後區分，而是按照間隔區分的，所以，在進行完這一輪的排序後，我們要保證以下資料是有序的，如下圖所示，不同顏色表示不同的子陣列，只要保證每個子陣列有序即可：

可以看到，每個子陣列的元素下標間隔都是inc，這就是inc值的意義。根據這一原則，我們就可以進行直接插入排序了，只需要依次將每個子陣列排好序即可。首先比較0和5位置的值，發現已經有序，無需交換，如下：

然後比較位置1和6，發現數值順序錯誤，對它進行交換，如下所示：

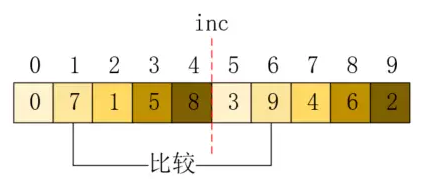接下來再依次比較2和7，3和8，4和9的值，將其排序，最終結果如下所示：

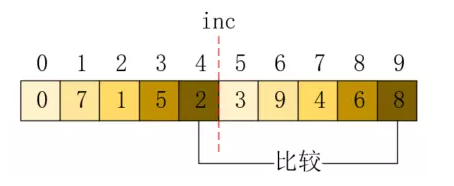現在，拆分的子陣列都已經是有序了。接下來，我們需要合併，我們把inc的值折半，再進行上述操作，那麼inc的位置和拆分的子陣列如下所示：

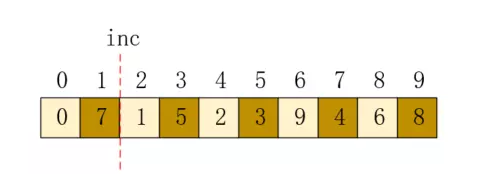可以看到，每個子陣列的元素下標間隔都和inc值一樣，這時子陣列只有兩個了。我們來對這兩個子資料依次進行直接插入排序，首先對包含位置0的陣列進行排序，直接插入排序就是把當前值插入到已有的有序子陣列中，所以0位置依然是0，然後把位置2的元素插入，因為1＞0，所以它的位置不變，如下所示：

位置4和6的元素又是最大值，所以也不需要交換，結果如下所示：

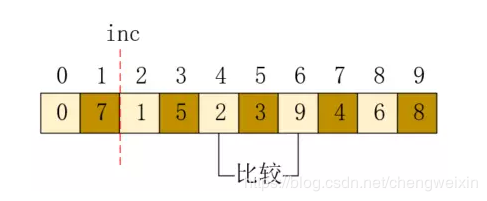接下來位置8，插入後需要和6交換，如下所示：

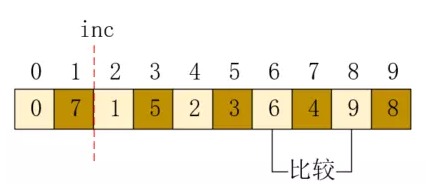這樣，第一個陣列就調整完畢了，接下來調整第二個陣列，位置1和3需要交換，如下所示：

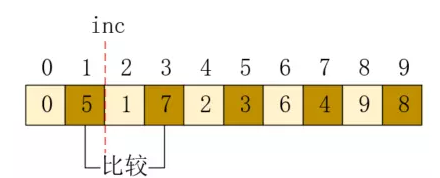接下來調整位置5，因為值3是最小值，應該放在位置1，所以需要把1和3位置的值向後移動，然後再插入，結果如下：

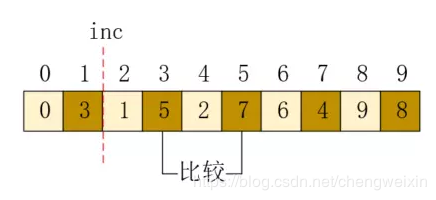最後位置7和9也按照同樣的方式進行，最終結果如下：

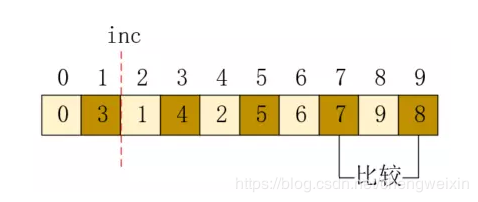現在，我們再進行合併時就是一個完整的陣列了，可以看到，這個陣列已經是基本有序的了，較小的值基本位於左側，較大的值基本位於右側，這比直接進行直接插入排序要好的多。希爾排序的程式碼如下：

p

rivate void shellSort(int[] arr){
    int len = arr.length;
    int inc = len;
    // 設定間隔值
    for (inc=len/2; inc>0; inc/=2) {
        // i 從inc走到len，j正好可以把所有子陣列遍歷一次
        // j會先比較每個子陣列的第一個值，再第二個值，這樣橫向進行遍歷
        for (int i = inc; i < len; i++) {
            for (int j = i; j>=inc && arr[j]<arr[j-inc]; j-=inc) {
                swap(arr,j,j-inc);
            }
        }
    }
}

希爾排序總體而言效率比直接插入排序要好，因為它最開始當inc值較大時，資料的移動距離很長，而當inc值小時，因為資料已經大致有序，可以使直接插入排序更有效率，這兩點是希爾排序高效必備的條件。inc值的選取對希爾排序十分關鍵，像以上這種折半方式，在某些情況下還是較慢，但是我們沒有辦法找到完美的計算方案使希爾排序最高效，以inc=inc*3+1構建的間隔也是常用的一種，示例程式碼如下：

private void shellSort1(int[] arr) {
    //首先根據陣列的長度確定增量的最大值
    int inc=1;
    // inc * 3 + 1得到增量序列的最大值
    while(inc <= arr.length / 3)
        inc = inc * 3 + 1;
    //進行增量查詢和排序
    while(inc>=1){           
        for(int i=inc;i<arr.length;i++){
            for(int j=i;j >= inc && arr[j] < arr[j-inc];j -= inc){
                swap(arr,j,j-inc);
            }
        }
        inc = inc/3;
    } 
}

目前，最高效的希爾排序的時間複雜度可以達到O(n3/2)，相關知識大家可以查閱書籍瞭解，這裡我們就不再追究了。

堆排序 堆排序是對簡單選擇排序的優化，在簡單選擇排序中，每排序一個數據，都要在剩餘全部資料中尋找最小值，但是在這個尋找的過程中，沒有對剩餘的資料記錄，所以之後的尋找會進行多次重複操作。堆排序則是會把這些資料記錄在堆中，之後的尋找只需要在堆中進行。

堆是具有下列性質的完全二叉樹：每個結點的值都大於或等於其左右孩子結點的值，稱為大頂堆；或者每個結點的值都小於或等於其左右孩子結點的值，稱為小頂堆。

根據以上定義，可以確定，根結點一定是最大（或最小）值。大頂堆和小頂堆示意如下：

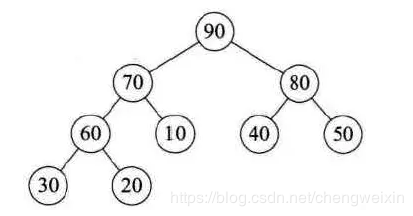
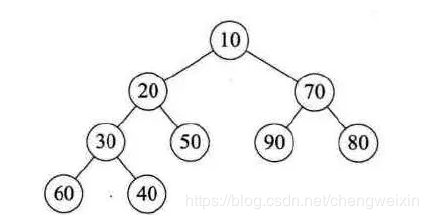如果按照層序遍歷的順序給堆的每個結點編號：0, 1, ..., (n-1)，那麼它一定符合以下條件：

a[i]≤a[2i+1] 且 a[i]≤a[2i+2]，其中0 ≤ i ≤ (n-1)/2，或 a[i]≥a[2i+1] 且 a[i]≥a[2i+2]，其中0 ≤ i ≤ (n-1)/2。

掌握了堆的概念之後，就可以進行堆排序了，以從小到大排序為例，它的過程是先將待排序的陣列構建成一個大頂堆，此時，根結點就是最大值，將它放置在陣列的結尾，然後將剩餘資料重新構建成一個堆，如此迴圈進行，直到全部有序。

那，我們如何構建一個大頂堆，又如何進行調整呢？接下來，我們用一個數組示例，來演示堆排序的過程，假如陣列如下：{50, 20, 90, 30, 80, 40, 70, 60, 10}，我們第一步要做的就是把它看做是一個完全二叉樹層序遍歷的結果集，所以它對應的完全二叉樹如下：

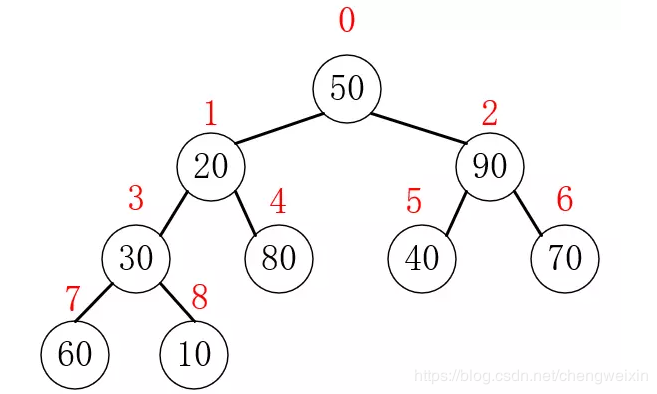我們要做的，就是把這棵完全二叉樹調整為一個大頂堆結構，按照樹的一般處理思路，我們只需要把每個子樹都調整為大頂堆，就可以把整棵樹調整為大頂堆，所以，我們只需要自下而上，依次把分別以3、2、1、0為根結點的子樹調整為大頂堆即可，結點3就是最後一個子樹，之後的結點都是葉子結點。

下面先看調整的程式碼，如下所示：

/**
 * 堆的調整
 * root：子樹的根結點位置
 * len：當前排序陣列的長度
 */
private void heapAdjust(int[] arr, int root, int len){
    if(len<=0)return;
    int temp;
    // 根結點的值先儲存
    temp = arr[root];
    // i是這個結點的左孩子，或者是它孩子的左孩子
    for (int i=2*root+1; i<len; i=2*i+1) {
        if(i<len-1 && arr[i]<arr[i+1]){
            // 尋找到兩個孩子的較大者
            i++;
        }
        // 根結點的值比兩個孩子都大，就不需要再調整了
        if(temp>=arr[i]){
            break;
        }
        // 把根結點的值記為這個較大的孩子的值
        arr[root] = arr[i];
        // 再向下一級子樹遍歷
        root=i;
    }
    // 最後把temp的值存放在空置的位置
    arr[root] = temp;
}

按照以上思路，這段程式碼看起來就比較簡單了，那就是尋找到這棵樹的最大值，並且每次都選擇它的兩個孩子中較大的那個進行交換，最終最大值處於根結點。有了調整的程式碼，我們就可以把原陣列構建成一個大頂堆了，只需要對結點3、2、1、0依次呼叫調整方法即可。如下所示：

for (int i = (len-2)/2; i>=0; i--) {
    heapAdjust(arr,i,len);
}

這裡要說明一下 i 的起點的設定，按照我們的定義，一個長度為 n 的陣列，其下標範圍是 0 到(n-1)，如果 n 是奇數，那麼最後一個有孩子的結點一定有兩個孩子，如上面這棵樹的結點3就有兩個孩子，如果 n 是偶數，那麼最後一個有孩子的結點只有一個左孩子。對於有兩個孩子的，我們用n-1-1，就得到了它左孩子的下標，對於只有一個孩子的，因為 n 是偶數，所以n-1是奇數，n-1-1還是偶數，可以知道(n-1)/2和(n-2)/2是相等的。綜上所述，我們使用(n-2)/2，就可以得到最後一個有孩子結點的下標。

現在，就可以實現完整的堆排序演算法了，只需要每次都把最大值移動到陣列最後，然後剩餘部分再進行一次調整即可，程式碼如下所示：

private static void heapSort(int[] arr){
    int len = arr.length;

    // 從最後一個有孩子的結點開始，逐一進行堆的調整
    for (int i = (len-2)/2; i>=0; i--) {
        heapAdjust(arr,i,len);
    }

// 對於一個堆，最大值一定在根結點，也就是在陣列位置0，把它換到陣列最後，然後對剩餘的資料再進行一次堆的調整
for (int i = len-1; i>0; i--) {
    // 把最大值放在陣列的最後
    swap(arr,0,i);

    // 剩餘的值進行堆的調整
    heapAdjust(arr,0,i);
}

} 堆排序的最壞時間複雜度為O(nlogn)，其中 n 是外層迴圈，logn是調整內部的for迴圈，這個for迴圈和遞迴類似。因為它對原始資料並不敏感，所以最好、平均和最壞時間複雜度都是O(nlogn)，和O(n2)相比效率高了很多。堆排序因為操作是在原地進行，所以空間複雜度為O(1)。

歸併排序 歸併排序也利用了完全二叉樹，從而把時間複雜度降低到O(nlogn)，它的思想是一種分而治之的思想，我們這裡以2路歸併排序為例，來說明它的核心原理。

假設初始序列含有 n 個記錄，則可以看成是 n 個有序的子序列，每個子序列的長度為1，然後兩兩歸併，得到n/2個長度為 2 或 1 的有序子序列；再兩兩歸併，...，如此重複，直至得到一個長度為 n 的有序序列為止，這種排序方法稱為2路歸併排序。

歸併排序的原理並不複雜，通過一張圖就可以完全理解它的意圖，如下所示，它的過程就是先分後治的分而治之思想的體現：

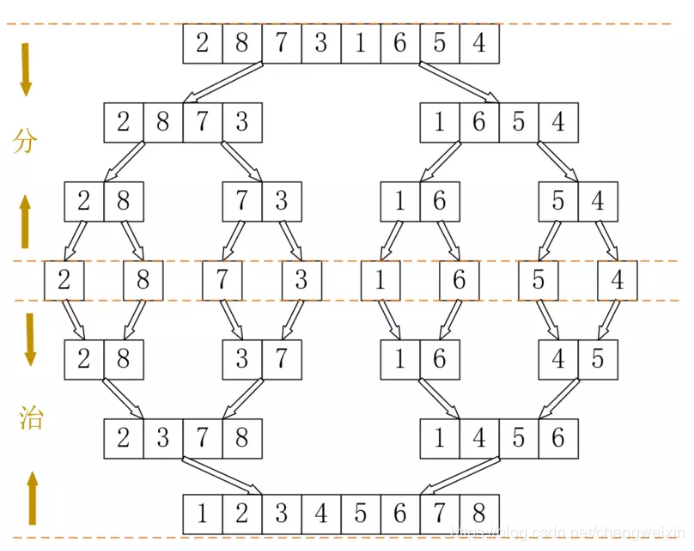分，就是把陣列拆分成一條一條資料，2路歸併就是採用二分法，直到每部分只含一條資料為止。治，就是把資料排序後再合併，從而使得每部分有序，再合併，直到全部有序為止。分的過程可以使用遞迴，這很好實現，程式碼如下所示：

private void mergeSort(int[] arr, int left, int right){
    if(left<right){
        int mid = (left+right)/2;
        mergeSort(arr,left,mid);
        mergeSort(arr,mid+1,right);
        // 歸併操作
        ...
    }
}

接下來就是治的過程，這個過程就是把兩個有序數組合併成一個有序陣列，以把{2, 8}和{3, 7}合併成{2, 3, 7, 8}為例，首先比較2和3，選擇2，如下所示：

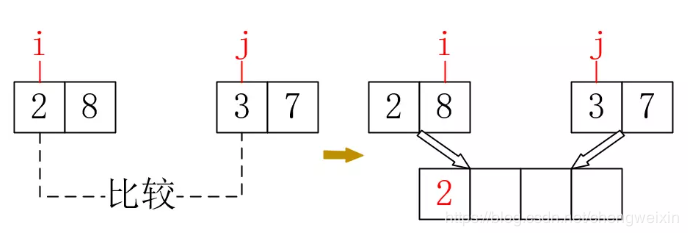接下來應該比較3和8，選擇3，如下所示：

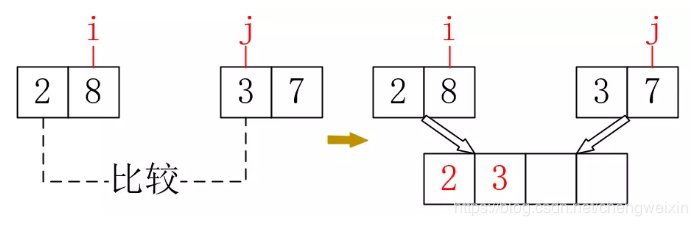接下來比較7和8，選擇7之後，只剩下8了，可以肯定8及之後（如果有）的所有資料都是比較大且有序的，無需再次比較。根據這個思路，參考程式碼如下所示：

private void merge(int[] arr, int[] temp, int left, int mid, int right){
    int i = left;
    int j = mid+1;
    int k = 0;
    while(i<=mid && j<=right){
        if(arr[i]<arr[j]){
            temp[k++] = arr[i++];
        }else{
            temp[k++] = arr[j++];
        }
    }

while(i<=mid){
    temp[k++] = arr[i++];
}
while(j<=right){
    temp[k++] = arr[j++];
}

k=0;
while (left<=right) {
    arr[left++] = temp[k++];
}

} 其中temp是事先建立好的陣列，因為陣列的特殊性，比較操作無法在原陣列進行，所以需要在temp陣列進行比較後，再將有序結果複製到原陣列。最終，歸併排序程式碼如下：

private void mergeSort(int[] arr){
    int[] temp = new int[arr.length];
    mergeSort(arr,temp,0,arr.length-1);
}

private void mergeSort(int[] arr, int[] temp, int left, int right){
    if(left<right){
        int mid = (left+right)/2;
        mergeSort(arr,temp,left,mid);
        mergeSort(arr,temp,mid+1,right);
        merge(arr,temp,left,mid,right);
    }
}

歸併排序的時間複雜度是O(nlogn)，而以上使用遞迴的做法，它的空間複雜度是O(n+logn)，其中 n 是temp陣列，logn是遞迴佔用的棧空間。可以看到，遞迴佔用了不菲的空間，那麼我們能不能用非遞迴的方式實現歸併排序呢？答案是肯定的，許多遞迴都可以轉為線性操作。歸併排序是從單個數據開始的，而陣列本身就可以看做是一個一個數據，非遞迴實現的思路如下：

其中不同顏色代表不同的子陣列，第一次從原陣列進行一次歸併後，temp陣列中存放的其實就是第二次歸併的原始資料，這時只要再從temp陣列歸併到原陣列，就得到了第三次歸併的原始資料，重複下去，直到歸併完畢。可以看到，只需要一個數組的空間就可以完成全部過程，所以空間複雜度降低到了O(n)。因為篇幅的原因，程式碼在文末github連結中，大家可以參考。

快速排序 快速排序：通過一趟排序將待排記錄分割成獨立的兩部分，其中一部分記錄的關鍵字均比另一部分記錄的關鍵字小，則可分別對這兩部分記錄繼續進行排序，以達到整個序列有序的目的。

從這段定義可以發現，這又是遞迴可以發揮能力的演算法，快速排序的關鍵在於用來分割的關鍵字的選擇。我們先從選擇每個子陣列最左側資料為例來實現快速排序，程式碼如下：

private void quickSort(int[] arr){
    qSort(arr,0,arr.length-1);
}

private void qSort(int[] arr, int low, int high) {
    int pivot;
    if(low<high){
        pivot = partition(arr,low,high);
        qSort(arr,low,pivot-1);
        qSort(arr,pivot+1,high);
    }
}

private int partition(int[] arr, int low, int high) {
    int pivotKey = arr[low];
    while (low<high) {
        while (low<high&&arr[high]>=pivotKey) {
            high--;
        }
        swap(arr,low,high);
        while (low<high&&arr[low]<=pivotKey) {
            low++;
        }
        swap(arr,low,high);
    }
    return low;
}

關鍵的程式碼就在partition這個方法中，先選擇一個關鍵字，然後用它左右兩側資料與之對比並調整位置，最後返回這個關鍵字的地址，再以此分為左右兩部分重複此操作。下面，我們用一個簡單的陣列來模擬以上操作，如下所示，紅色標註的資料就是選擇的關鍵字：

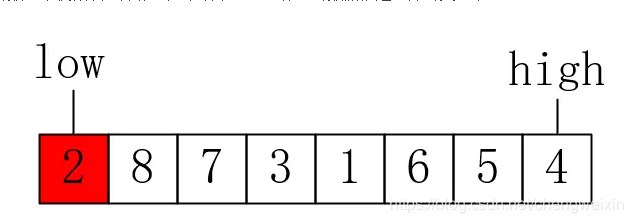先比較high的值與關鍵字，如果不需要調整，就向前移動，如下所示：

接下來5和6都比關鍵字大，直到high的值為1時，交換low與high的值，注意我們的關鍵字還是2，如下所示：

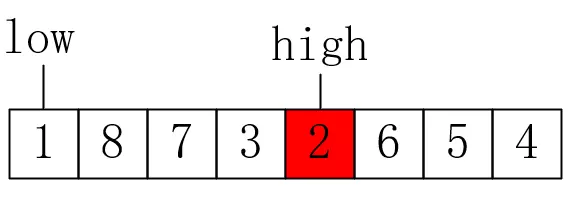接下來比較low的值與關鍵字，1比2小，所以low指標後移，如下所示：

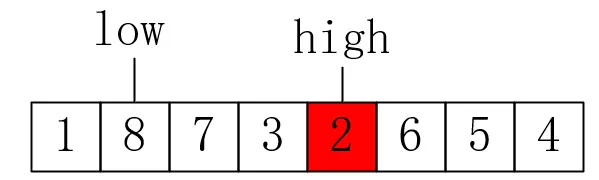接下來8比2大，所以交換low和high的值，如下所示：

交換low和high 接下來直到high指向 7 都不再進行交換，第一輪排序就結束了，可以看到，low的值依然是之前的關鍵字。這也是為何先比較high指標再比較low指標的原因，也是為何最終返回low的原因。接下來只要按照這個規則，就可以把陣列排序好。

快速排序最好的時間複雜度為O(nlogn)，也就是每次關鍵字取值都能恰好把陣列平分兩部分時的情況，最壞時間複雜度是O(n2)，也就是十分不幸地，每次拆分都分成了一邊空一邊是剩餘全部的兩部分。而空間複雜度也跟隨著變化，從O(logn)到O(n)。

可以看到，快速排序嚴重受關鍵字選擇的影響，像以上示例關鍵字2僅把陣列分成了一邊長度為1、一邊長度為6的兩部分，顯然不夠高效。於是就有了三數取中法，做法是取三個關鍵字先進行排序，然後用中間的值作為選擇的關鍵字，這樣的好處是這個關鍵字至少不是最大值或最小值，而且很有可能取到比較接近中間的值，這在大多數情況下都能提高一定的效率。三數取中法只需要在partition中增加以下程式碼即可：

private static int partition(int[] arr, int low, int high) {
    // 三數取中法,把中間值存放在low中
    int mid = low + (high-low)/2;
    if (arr[low]>arr[high]) {
        swap(arr, low, high);
    }
    if (arr[mid]>arr[high]) {
        swap(arr,mid,high);
    }
    if (arr[low]>arr[mid]) {
        swap(arr,low,mid);
    }

    int pivotKey = arr[low];
    ...
}

當然，三數取中法並不完美，它有可能很高效也可能很低效，這點就需要根據實際情況來合理選擇了，甚至有人提出採用九數取中法來進一步提高效率，感興趣的話可以查閱相關資料進一步研究。接下來我們對快速排序的其他部分進行優化，在排序過程中，選取的關鍵字從最初到最終的位置經過了多次移動，這是沒有必要的，可以讓它直接到達終點，修改程式碼如下所示：

private int partition(int[] arr, int low, int high) {
    int pivotKey = arr[low];
// 暫存關鍵字
int temp = pivotKey;

while (low<high) {
    while (low<high&&arr[high]>=pivotKey) {
        high--;
    }
    arr[low] = arr[high];
    //swap(arr,low,high);
    while (low<high&&arr[low]<=pivotKey) {
        low++;
    }
    arr[high] = arr[low];
    // swap(arr,low,high);
}
// 恢復關鍵字
arr[low] = temp;
return low;

} 以上優化用複製資料代替了交換資料，從而使效能有一定的提升，可以這樣做的原因是因為每次進行交換的值都包含關鍵字。除此之外，它的遞迴部分也可以進行優化，優化後的程式碼如下所示：

private void qSort(int[] arr, int low, int high) {
    int pivot;
    // 遞迴
    // if(low<high){
    //     pivot = partition(arr,low,high);
    //     qSort(arr,low,pivot-1);
    //     qSort(arr,pivot+1,high);
    // }
    // 迭代代替遞迴
    while(low<high){
        pivot = partition(arr,low,high);
        qSort(arr,low,pivot-1);
        low = pivot+1;
    }
}

這個優化就是用迴圈代替了遞迴，只是寫法上有些不同，是否真的有優化效果還有待考證。關於遞迴和迴圈，也不一定是所有遞迴都應該使用迴圈代替，這裡有一篇文章我覺得分析的不錯，大家可以參考一下，連結如下：快速排序的優化和關於遞迴的問題，說說我的想法。

分配排序 最後，我們還要講一個應用場景較少的排序演算法，它的時間複雜度可以達到線性階，也就是O(n)。根據不同的分配方式，又主要有計數排序、桶排序和基數排序三個演算法。

1. 計數排序 計數排序的原理很簡單，顧名思義就是對每個資料計數，然後分配到下標為0-max的陣列中，然後對計數進行排列即可。如下所示，桶中儲存的是每個資料出現的次數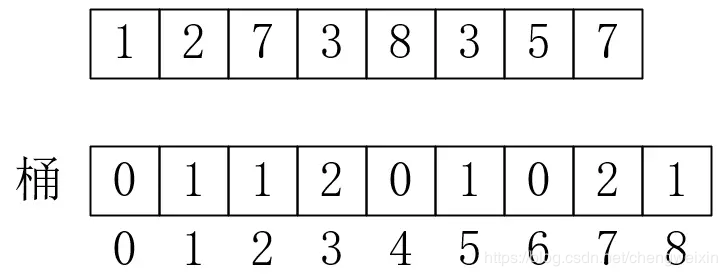： 計數 有了計數，就可以得到排好序的陣列了，0有0個，1有1個，所以第一個有序值是1，2有一個，所以第二個值是2，依次類推，最後有序陣列為{1, 2, 3, 3, 5, 7, 7, 8}。實現程式碼如下：

   private void countingSort(int[] arr){ int len = arr.length; // 獲取最大值 int max = arr[0]; for (int i = 1; i < len; i++) { if(max<arr[i]){ max = arr[i]; } } // 建立max+1個桶，從0-max int[] bucket = new int[max+1]; for (int i = 0; i < len; i++) { // 每獲取一個數，就把它放在編號和其一致的桶中 bucket[arr[i]]++; } int j = 0; for (int i = 0, bLen = bucket.length; i < bLen; i++) { // 遍歷桶，按順序恢復每條資料 for (int k = bucket[i]; k > 0; k--) { arr[j++] = i; } } }

因為一般重複資料比較少，所以每個桶內的值不會很大，它的最好時間複雜度是O(n)。但是它有很嚴格的使用條件，那就是值是離散的，有窮的，而且資料要緊密，比如有陣列{0, 2, 5, ..., 10000}，其中10000與其他資料差距很大，那麼就會造成嚴重的空間浪費，也給遍歷增加了難度。但是如果資料能滿足這些要求，它的排序速度非常快。

2. 桶排序 桶排序和計數排序類似，只是不再精確地一個下標對應一個數組，而是取多個區間，比如[0, 10), [10, 20), ...，然後每個部分再使用如直接插入排序等方法進行排序。這一點和雜湊表類似，需要陣列和連結串列結合使用，如下所示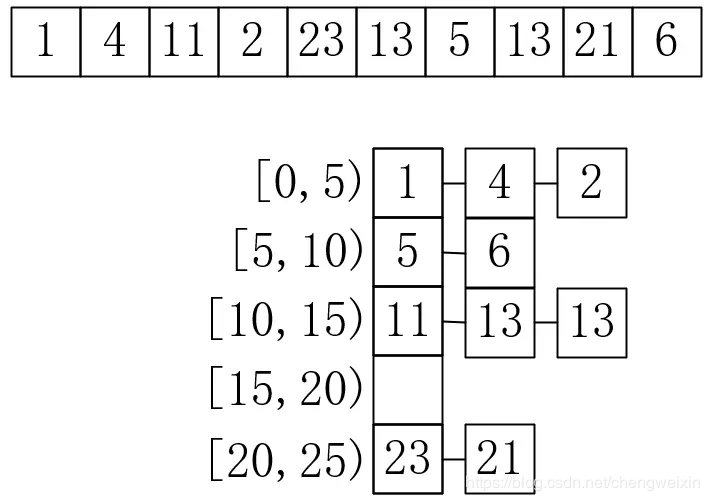： 桶排序 陣列的每一位儲存的都是連結串列，對這個連結串列進行排序比對全部資料排序要好的多，這裡就不再給出程式碼實現了。

3. 基數排序 基數排序，就是從每個數的低位開始排序，先排序個位數，再排序十位數、百位數，直至整個陣列有序。它的原理如下所示，首先按照個位排序：

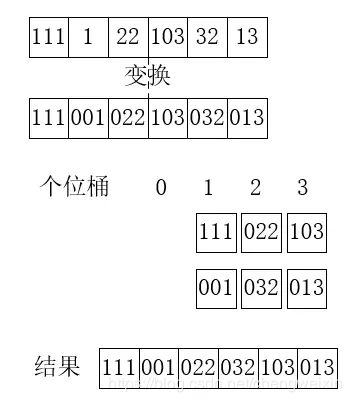根據個位排序的結果，再進行十位數排序，如下所示：

最後再按照百位數排序，如下所示：

4. 總結 分配排序針對整數這種結構，在資料較為均勻，緊密性較好的前提下進行了優化，可以使得排序時間複雜度接近O(n)。不過因為它的使用場景較少，且佔用空間比較多，因此不常被使用。

總結 除了分配排序這種十分苛刻的排序演算法，其他排序的時間複雜度都在O(nlogn)到O(n2)之間。快速排序是當前使用最多的一種排序演算法，但是我們也不能盲目的選擇它，而是要針對實際情況選擇不同的演算法。通常，當資料量十分小（一般是7-10個）時，會使用直接插入排序來代替其它排序，因為當資料很少時，演算法的時間複雜度並不能作為評判演算法效率的唯一標準，時間複雜度本身比較粗略，在 n 很小時有可能O(n2)比O(n)還要快，比如n=5，O(n2)演算法實際執行次數是n2=25次，而O(n)演算法實際執行次數是10n=50次，這時候常數項也會對演算法有所影響。

最後，我們對多種排序的綜合性能進行對比，如下表所示：

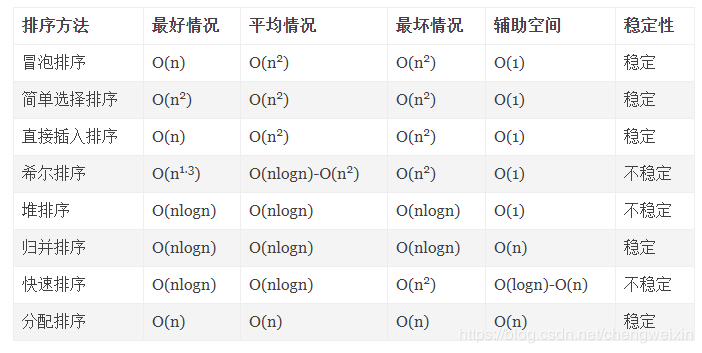最後，再對這裡的穩定性簡單說明一下，對於兩兩比較的演算法一定是穩定的，而存在跳躍比較的演算法則是不穩定的，因為兩兩比較的是相鄰值，那麼相等的資料不會發生交換，而跳躍比較就無法保證了，所以如果對穩定性要求很高，可能歸併排序就是最好的選擇。

以上就是常見排序演算法的全部解析了，經歷了這麼多年，還誕生了更多更有趣的排序演算法，以後有機會再來一睹為快吧。

QQ討論群組：984370849 706564342 歡迎加入討論

想要深入學習的同學們可以加入QQ群討論，有全套資源分享，經驗探討，沒錯，我們等著你，分享互相的故事!

相關推薦