作為GISer，處理空間資料才是主要任務，向量資料壓縮這一塊要學習學習。

這裡向量資料壓縮是指線的資料壓縮，意思是假如某根線有n個點，現在如果刪除一些點，這條線仍然性質良好，那麼就實現了壓縮，那麼下面的演算法目的就是對線上不必要一些點給刪除了。

演算法名字叫道格拉斯——普克法演算法，當然還有還有其他演算法，學習這個演算法原因是它使用了遞迴，其實很早以前就嘗試寫這個演算法，無奈當時只會些順序迴圈之流，苦悶數日不得其解，如今終有機會手刃此題，甚歡！

演算法描述：
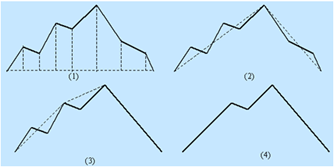
對每一條曲線的首末點虛連一條直線，求所有點與直線的距離，並找出最大距離值dmax，用dmax與限差D相比：
若dmax＜D，這條曲線上的中間點全部捨去；
若dmax≥D，保留dmax對應的座標點，並以該點為界，把曲線分為兩部分，對這兩部分重複使用該方法。

純C程式碼：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

typedef struct//點的資料結構
{
    double x;
    double y;
    int tag;//判斷此點是否保留標誌，1保留，0不保留
}Point;


///getmax是獲取最大距離與最大距離所對應點標號函式
void getmax(double *dmax,int *dmax_tag,Point point[],int left,int right)
{
    *dmax=-1;//初始化個小值
 

    int i;
    double distance;
    double k=(point[left].y-point[right].y)/(point[left].x-point[right].x);//不考慮斜率不存在的無聊情況
    double b=point[left].y-k*point[left].x;
    //點到直線距離公式：(k*x-y+b)/√(k*k+1)
    for(i=left+1;i<=right-1;i++)
    {
        distance=fabs((k*point[i].x-point[i].y+b)/sqrt((k*k+1))
 
);
        if(distance>=*dmax)
        {
            *dmax=distance;
            *dmax_tag=i;
        }
    }
}

///道格拉斯——普克法演算法
void fun(Point point[],int left,int right,double Dis)
{
    if(left>=right-1)///少於三個點就退出了
    {
        return;
    }
    else
    {
        double dmax;//最大高度
        int dmax_tag,i;//最大高度對應的點號
        getmax(&dmax,&dmax_tag,point,left,right);//把dmax,dmax_tag指標傳進去為了返回來
        if(dmax<Dis)//捨去
        {
            for(i=left+1;i<=right-1;i++)
            {
                point[i].tag=0;//置捨去了的以0標記
            }
        }
        else
        {
            ///遞迴，並以dmax_tag點為界，把曲線分為兩部分，對這兩部分重複使用該方法
            fun(point,left,dmax_tag-1,Dis);
            fun(point,dmax_tag+1,right,Dis);
        }
    }
}