劍指offer-12:數值的整數次方
阿新 • • 發佈:2018-12-05
題目描述
給定一個double型別的浮點數base和int型別的整數exponent。求base的exponent次方。
思路
個人覺得此題考查的是快速冪演算法。
快速冪演算法
快速冪 , 矩陣快速冪 在算大指數次方時是很高效的,他的基本原理是二進位制。
大家首先要認識到這一點:任何一個整數N,都能用二進位制來表示。。
那麼對於an , n一定可以用二進位制表示,比如a11
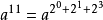
double fun( double a, int b )
{
double r = 1;
double base = a;
while 此題程式碼
public class Solution12 {
public double Power(double base, int exponent) {
double 