資料結構--圖論
目錄
(1)DFS(Deep First Search 深度優先搜尋)
(2)BFS(Breadth First Search 寬度優先搜尋&廣度優先搜尋)
(1)最小生成樹(MST-Minimum Spanning Tree)
一、圖的基本知識
- 圖:是由資料元素的集合及資料元素之間的關係集合組成的一種資料結構,G=(V,E),其中V是頂點集,E是邊集
- 無向圖:如果頂點之間沒有方向,稱為無向圖,無向圖的邊表示一般用圓括號(v,w)
- 有向圖:如果頂點之間有方向,就稱為有向圖,有向圖的邊表示一般用尖括號<v,w>,又稱為弧
- 完全圖:在有n個頂點的無向圖中,有n(n-1)/2條邊,稱此圖為完全無向圖;在有n個頂點的有向圖中,有n(n-1)條邊,則稱此圖 為完全有向圖(每一個頂點與另外n-1個頂點都有編項鍊)
- 權:邊上具有與它相關的係數,即稱為權,帶權圖也被稱為網路
- 鄰接點:如果(v,w)是無向圖G的一條邊,則稱V與W互為鄰接頂點;如果<v,w>是有向圖G中的一條弧,則稱頂點v鄰接到頂點到w(v是w的前驅),頂點w鄰接自v(w是v的後繼)
- 子圖:設圖G=(V,E)和圖G'=(V',E')。若V'屬於V,E'屬於E,則稱圖G'是圖G的子圖
- 頂點的度:無向圖中,頂點V的度表示依附於V的邊數,記作TD(v);有向圖中,以頂點v為始點的有向邊的條數稱為v的出度,記 作OD(v),以頂點v為終點的有向邊的條數稱為v的入度,記作ID(v),有向圖中頂點v的度等於該頂點的入度與出度之和:TD(v)=ID(v)+OD(v)
- 路徑:在圖G=(V,E)中,從頂點vi出發,沿一些邊或弧經過一些頂點Vp1,Vp2.....,到達頂點vj,則稱頂點序列(vi,vp1,vp2.....vj)為從打頂點vi到頂點vj的路徑
- 路徑長度:對於不帶權的圖,路徑長度是指此路徑上邊的數目;帶權圖,路徑長度是指路徑上各邊的權之和
- 簡單路徑和迴路:對於一套路徑,若路徑上各頂點均不相同,則稱該路徑為簡單路徑;若頂點上第一個頂點和最後一個頂點相同,則稱該路徑為迴路或環
- 連通圖和連通分量:在無向圖中,若從頂點vi到vj有路徑,則稱頂點vi與vj使連通的,如果無向圖中任意兩個頂點都是連用的,則稱此無向圖為連通圖。非連通圖的極大連通子圖(包含所有連通的頂點和這些頂點依附的所有的邊)叫做連通分量
- 強連通圖和強連通分量:在有向圖中,若對於頂點vi和vj,存在一條從vi到vj和從vj到vi的路徑,則稱頂點vi和頂點vj時強連通。如果有向圖中任意兩個頂點都是強連通的,則稱此有向圖為強連通圖。非強連通圖的極大強連通子圖叫做強連通分量
- 生成樹:一個連通圖的生成樹是它的極小連通子圖(包含圖中全部n個頂點及使這些頂點連通的n-1條
二、圖的儲存結構
(1)鄰接矩陣
對於帶權圖可表示
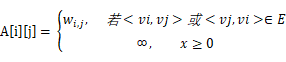
鄰接矩陣儲存表示
#define MaxInt 32768 //表示極大值, 即
#define MVNum //最大頂點
typedef char VerTexType; //設頂點的資料型別為字元型
typedef int ArcType; //設邊的權值為整形
typedef struct
{
VerTexType vexs[MVNum]; //頂點表
ArcType arcs[MVNum][MVNum] //鄰接矩陣
int vexnum, arcnum //頂點數、邊數
}AMGraph;/*
確定頂點vex在圖G中的位置
*/
int LocateVex(AMGraph G, VerTexType vex)
{
for(int i = 0; i < G.vexnum; i ++)
if(vex == G.vexs[i])return i;
}
/*
以無向帶權圖為例
*/
void CreateUDN(AMGraph &G)
{
cout<<"請輸入頂點和邊的數目:"<<endl;
cin>>G.vexnum>>G.arcnum;
//對無向圖初始化
for(int i = 0; i < G.vexnum; i ++)
{
for(int j = 0; j < G.vexnum; j ++)
{
G.arcs[i][j] = MaxInt;
}
}
cout<<"請輸入頂點:"<<endl;
for(int i = 0; i < G.vexnum; i ++)cin>>G.vexs[i];
cout<<"請輸入邊:"<<endl;
for(int i = 0; i < G.arcnum; i ++)
{
VerTexType u, v;
ArcType w;
cin>>u>>v>>w;
int uid = LocateVex(G, u), vid = LocateVex(G, v);
G.arcs[uid][vid] = G.arcs[vid][uid] = w;
}
}鄰接矩陣優缺點:
優點:
直接判斷兩點是否右邊相連
方面計算個點的度(入度與出度)
缺點:
不便增加和刪除頂點
不便統計邊的數目
空間複雜度高O(n^2),浪費空間
綜上:鄰接矩陣適用於稠密圖
(2)鄰接表
typedef char VerTexType; //頂點的資料型別
typedef int ArcType; //邊的權值的資料型別
typedef struct ArcNode //定義邊節點
{
int adjvex; //指向下一個頂點的位置
int val; //邊的的權值
struct ArcNode *nextarc; //指向下一個邊的指標
// OtherInfo inof;
}ArcNode;
typedef struct VNode //定義每一個頂點
{
VerTexType data; //頂點表示的值
ArcNode *firstarc; //指向第一條依附於該頂點的邊的指標
}VNode, AdjList[MVNum]; //鄰接表
typedef struct //定義圖
{
AdjList vertices; //圖的頂點
int vexnum, arcnum; //圖的頂點數、邊數
}ALGraph;/*
以無向帶權圖圖為例
*/
void CreateUDN(ALGraph &G)
{
ArcNode *pu, *pv;
cout<<"請輸入頂點和邊的數目:"<<endl;
cin>>G.vexnum>>G.arcnum;
cout<<"請輸入頂點:"<<endl;
for(int i = 0; i < G.vexnum; i ++)
{
cin>>G.vertices[i].data;
G.vertices[i].firstarc = NULL; //將改頂點的表頭指標域置為NULL
}
cout<<"請輸入邊:"<<endl;
for(int i = 0; i < G.arcnum; i ++)
{
VerTexType u, v;
int w;
cin>>u>>v>>w;
int uid = LocateVex(G, u), vid = LocateVex(G, v);
pu = new ArcNode; pv = new ArcNode;
pu->adjvex = vid; pu->val = w;
pu->nextarc = G.vertices[uid].firstarc; G.vertices[uid].firstarc = pu;
// //無向圖
pv->adjvex = uid; pv->val = w;
pv->nextarc = G.vertices[vid].firstarc; G.vertices[vid].firstarc = pv;
}
}
鄰接表的優缺點:
優點:
便於增加和刪除頂點
便於統計邊的數目
空間效率高
缺點:
不便於判斷頂點與頂點之間是否存在邊
不便於計算圖各頂點的度
綜上:鄰接表使用稀疏圖
三、圖的遍歷方式
(1)DFS(Depth First Search 深度優先搜尋)
類似於樹的先序遍歷,用遞迴實現,其思路於下:
a.從圖中某一頂點v出發,訪問v;
b.找出剛訪問的頂點的第一個未被訪問的鄰接點,訪問該頂點。以該頂點為新起點,重複此操作,直至剛訪問過得頂點中沒有未被訪問的鄰接點為之;
c.返回前一個訪問過的且仍有未被訪問的鄰接的頂點,
d.重複操作b和c, 直至圖中所有頂點都被訪問過,結束搜尋。
程式碼實現
/*
以儲存方式為鄰接矩陣的無向圖為例
新定義陣列 visited[MVNum]
visited[i] = 0 表示序號為i的頂點未被訪問
visited[i] = 1 表示序號為i的頂點已被訪問
*/
void DFS(AMGraph G, VerTexType vert)
{
int vid = LocateVex(G, vert);
visited[vid] = 1; cout<<vert<<" ";
for(int i = 0; i < G.vexnum; i ++)
{
if(!visited[i] && G.arcs[vid][i])DFS(G, G.vexs[i]);
}
}(2)BFS(Breadth First Search 寬度優先搜尋&廣度優先搜尋)
類似於樹的按層次遍歷的過程,用佇列實現,其過程於下
a.從圖的一個頂點v出發, 訪問該點;
b.以此訪問頂點v的各個未被訪問的鄰接點;
c.分別從這些鄰接點出發依次訪問他們的鄰接點,重複此操作,直至所有已被訪問的頂點的鄰接點都被訪問到。
程式碼實現
/*
以儲存方式為鄰接矩陣的無向圖為例
為方便,使用C++STL中已整合好的佇列queue
同時使用visited[MVNum]陣列, 標記頂點的訪問情況
*/
void BFS(AMGraph G, VerTexType v)
{
//以頂點v為起始點
for(int i = 0; i < MVNum; i ++)visited[i] = 0; //將所有頂點初始化為未訪問
queue<VerTexType>que;
que.push(G.vexs[v]);
while(!que.empty())
{
VerTexType vert = que.front(); que.pop();
int vid = LocateVex(G, vert);
if(!visited[vid]) //若頂點vert未被訪問
{
visited[vid] = 1;
cout<<vert<<" ";
for(int i = 0; i < G.vexnum; i ++)
{
if(!visited[i] && G.arcs[vid][i])que.push(G.vexs[i]);
}
}
}
}
(3)略談DFS與BFS其他用途
二者都可用於求圖的連通度
最短路問題一般用BFS實現
其他用途可查略其他資料
四、圖的應用
(1)最小生成樹(MST-Minimum Spanning Tree)
1.普里姆演算法(Prim)
思想:
a.從圖中一點v出發,選擇與點v相鄰的權值最小的邊,將其加入MST的頂點集合U中;
b.再從集合U出發,將不再集合U中且與集合U相連的各邊中權值最小的邊加入集合U中;
c.重複操作b,知道所有頂點都加入集合U中。
程式碼實現:
/*
鄰接矩陣儲存的無向帶權
*/
#include <bits/stdc++.h>
using namespace std;
#define MaxInt 32768
#define MVNum 100
typedef char VerTexType ;
typedef int ArcType;
typedef struct
{
VerTexType vexs[MVNum];
ArcType arcs[MVNum][MVNum];
int vexnum, arcnum;
}AMGraph;
struct closedge
{
ArcType cost;
int adjvex;
}ClosEdge[MVNum];
int LocateVex(AMGraph G, VerTexType v)
{
for(int i = 0; i < G.vexnum; i ++)
{
if(G.vexs[i] == v)return i;
}
}
//建立無向帶權圖
void CreateUDN(AMGraph &G)
{
cout<<"輸入頂和邊的數目:"<<endl;
cin>>G.vexnum>>G.arcnum;
for(int i = 0; i < G.vexnum; i ++)cin>>G.vexs[i];
for(int i = 0; i < G.vexnum; i ++)
{
for(int j = 0; j < G.vexnum; j ++)
{
G.arcs[i][j] = MaxInt;
}
}
VerTexType u, v;
ArcType w;
for(int i = 0; i < G.arcnum; i ++)
{
cin>>u>>v>>w;
int uid = LocateVex(G, u), vid = LocateVex(G, v);
G.arcs[uid][vid] = G.arcs[vid][uid] = w;
}
}
void Prim(AMGraph G, VerTexType v)
{
int visited[MVNum]; //記錄頂點是否被訪問
for(int i = 0; i < G.vexnum; i ++) visited[i] = 0;
int vid = LocateVex(G, v);
visited[vid] = 1;
int Min;
//初始化
for(int i = 0; i < G.vexnum; i ++)
{
if(!visited[i])
{
ClosEdge[i].cost = G.arcs[vid][i];
ClosEdge[i].adjvex = vid;
}
}
int u;
ArcType res = 0;
for(int i = 1; i < G.vexnum; i ++)
{
Min = MaxInt;
//找出權值最小的邊
for(int j = 0; j < G.vexnum; j ++)
{
if(!visited[j] && ClosEdge[j].cost < Min)
{
Min = ClosEdge[j].cost;
u = j;
}
}
res += ClosEdge[u].cost;
cout<<G.vexs[ClosEdge[u].adjvex]<<" <---> "<<G.vexs[u]<<" = "<<ClosEdge[u].cost<<endl;
visited[u] = 1;
//更新最小邊
for(int j = 0; j < G.vexnum; j ++)
{
if(!visited[j] && G.arcs[u][j] < ClosEdge[j].cost)
{
ClosEdge[j].cost = G.arcs[u][j];
ClosEdge[j].adjvex = u;
}
}
}
cout<<"the MST is = "<<res<<endl;
}
int main()
{
AMGraph G;
CreateUDN(G);
Prim(G, G.vexs[2]);
return 0;
}
/*
測試樣例
6 10
1 2 3 4 5 6
1 2 5
1 4 7
2 3 4
3 1 8
3 6 9
4 3 5
4 6 6
5 4 5
6 1 3
6 5 1
6 8
A B C D E F
A B 3
B E 7
C B 2
C F 1
D A 4
D E 8
D F 1
F E 5
*/
2.克魯斯卡爾演算法(Kruskal)
思想:
a.將左右邊按權值從小到大排序;
b.依次選取選取權值小的邊,若該邊的兩個頂點均在MST集合U中,則放棄次邊,否則將次邊加入集合U中
c.重複操作c,直至所選的邊數等於頂點的數目減一結束。
程式碼實現:
使用並查集,兩個操作
a.判斷邊的兩個頂點是否擁有相同祖先(即兩個頂點是否同在集合U中)
b.合併邊的兩個頂點的公共祖先(即將兩個頂點加入集合U中)
#include <bits/stdc++.h>
using namespace std;
/*
鄰接矩陣實現無向帶權圖的最小生成樹
*/
#define MaxInt 32768
#define MVNum 100
typedef char VerTexType;
typedef int ArcType;
int father[MVNum]; //記錄頂點的祖宗節點
int NumEdge; //記錄邊的數目
typedef struct
{
VerTexType vexs[MVNum];
ArcType arcs[MVNum][MVNum];
int vexnum, arcnum;
}AMGraph;
//克魯斯卡爾演算法
struct ArcEdge //定義邊
{
int head, tail; //邊的頭和尾
ArcType cost; //邊的權值
}Edge[MVNum * MVNum];
//按邊的從小到大排序
bool cmp(const ArcEdge &a, const ArcEdge &b)
{
return a.cost < b.cost;
}
//新增邊
void AddEdge(int u, int v, ArcType w)
{
Edge[NumEdge].head = u;
Edge[NumEdge].tail = v;
Edge[NumEdge].cost = w;
NumEdge ++;
}
//獲取父節點
int GetFather(int a)
{
return father[a] == a ? a : GetFather(father[a]);
}
//合併兩個節點
void Unionn(int x, int y)
{
father[GetFather(x)] = GetFather(y);
}
int LocateVex(AMGraph G, VerTexType vex)
{
for(int i = 0; i < G.vexnum; i ++)
if(vex == G.vexs[i])return i;
}
//建立一個圖
void CreateUDN(AMGraph &G)
{
cout<<"請輸入頂點和邊的數目:"<<endl;
cin>>G.vexnum>>G.arcnum;
//對無向圖初始化
for(int i = 0; i < G.vexnum; i ++)
{
for(int j = 0; j < G.vexnum; j ++)
{
G.arcs[i][j] = MaxInt;
}
}
cout<<"請輸入頂點:"<<endl;
for(int i = 0; i < G.vexnum; i ++)cin>>G.vexs[i];
cout<<"請輸入邊:"<<endl;
for(int i = 0; i < G.arcnum; i ++)
{
VerTexType u, v;
ArcType w;
cin>>u>>v>>w;
int uid = LocateVex(G, u), vid = LocateVex(G, v);
G.arcs[uid][vid] = G.arcs[vid][uid] = w;
/*
此處即為克魯斯卡爾演算法的建邊
因為是無向圖,要建兩次邊
*/
AddEdge(uid, vid, w);
AddEdge(vid, uid, w);
}
}
void Kruskal(AMGraph G)
{
//初始化個頂點的祖宗節點為本身,即初始各個頂點互不相連
sort(Edge, Edge + NumEdge, cmp); //按邊排序
for(int i = 0; i < G.vexnum; i ++)father[i] = i;
int tot = 0;
ArcType res = 0;
for(int i = 0; i < NumEdge; i ++)
{
int head = Edge[i].head;
int tail = Edge[i].tail;
ArcType cost = Edge[i].cost;
if(GetFather(head) == GetFather(tail))continue;
//如何該邊的兩個頂點的祖宗節點相同,則說明這兩個頂點屬於一個集合,所以要跳出迴圈
//否則該邊可以作為生成樹的一條邊
cout<<G.vexs[head]<<"<-->"<<G.vexs[tail]<<" = "<<cost<<endl;
Unionn(head, tail);
tot ++; res += cost;
if(tot == G.vexnum - 1)break;
}
cout<<"the MST is "<<res<<endl;
}
int main()
{
AMGraph G;
NumEdge = 0;
CreateUDN(G);
Kruskal(G);
return 0;
}
/*
測試樣例
6 10
1 2 3 4 5 6
1 2 5
1 4 7
2 3 4
3 1 8
3 6 9
4 3 5
4 6 6
5 4 5
6 1 3
6 5 1
6 8
A B C D E F
A B 3
B E 7
C B 2
C F 1
D A 4
D E 8
D F 1
F E 5
*/
3.演算法分析
分析:Prim演算法的複雜度為O(n^2),適用於稠密圖
Kruskal演算法複雜度為O(n + e)使用稀疏圖
(2)最短路徑
1.迪傑斯特拉演算法(Dijkstra)
#include <bits/stdc++.h>
using namespace std;
#define MaxInt 32768
#define MVNum 100
typedef char VerTexType ;
typedef int ArcType;
typedef struct
{
VerTexType vexs[MVNum];
ArcType arcs[MVNum][MVNum];
int vexnum, arcnum;
}AMGraph;
int LocateVex(AMGraph G, VerTexType v)
{
for(int i = 0; i < G.vexnum; i ++)
{
if(G.vexs[i] == v)return i;
}
}
//建立無向帶權圖
void CreateUDN(AMGraph &G)
{
cout<<"輸入頂和邊的數目:"<<endl;
cin>>G.vexnum>>G.arcnum;
for(int i = 0; i < G.vexnum; i ++)cin>>G.vexs[i];
for(int i = 0; i < G.vexnum; i ++)
{
for(int j = 0; j < G.vexnum; j ++)
{
G.arcs[i][j] = MaxInt;
}
}
VerTexType u, v;
ArcType w;
for(int i = 0; i < G.arcnum; i ++)
{
cin>>u>>v>>w;
int uid = LocateVex(G, u), vid = LocateVex(G, v);
G.arcs[uid][vid] = G.arcs[vid][uid] = w;
}
}
void Dijkstra(AMGraph G, VerTexType v)
{
int visited[MVNum], lowcost[MVNum], pre[MVNum];
//pre[j]表示到頂點j前驅
int vid = LocateVex(G, v);
for(int i = 0; i < G.vexnum; i ++)
{
lowcost[i] = MaxInt; pre[i] = -1; visited[i] = 0;
}
lowcost[vid] = 0;
int u;
while(1)
{
u = -1;
//找較小的路徑
for(int v = 0; v < G.vexnum; v ++)
{
if(!visited[v] && (u == -1 || lowcost[v] < lowcost[u]))
{
u = v;
}
}
if(u == -1)break;
visited[u] = 1;
cout<<G.vexs[u]<<" "<<lowcost[u]<<endl;
//更新路徑
for(int v = 0; v < G.vexnum; v ++)
{
if(!visited[v] && (lowcost[v] > lowcost[u] + G.arcs[u][v]))
{
lowcost[v] = lowcost[u] + G.arcs[u][v];
pre[v] = u;
}
}
}
int path[MVNum];
//回溯最短路的路徑
for(int i = 0; i < G.vexnum; i ++)
{
if(vid == i)continue;
int t = i, ans = 0;
while(pre[t] != -1)
{
path[ans++] = pre[t];
t = pre[t];
}
cout<<"to the vert the "<<G.vexs[i]<<": "<<
"shortest distance = "<<lowcost[i]<<endl;
cout<<"the shortest path is ";
for(int j = ans - 1; j >= 0; j--)cout<<G.vexs[path[j]]<<" ";
cout<<endl<<endl;
}
}
int main()
{
AMGraph G;
CreateUDN(G);
Dijkstra(G, G.vexs[4]);
return 0;
}
/*
6 10
1 2 3 4 5 6
1 2 5
1 4 7
2 3 4
3 1 8
3 6 9
4 3 5
4 6 6
5 4 5
6 1 3
6 5 1
6 8
A B C D E F
A B 3
B E 7
C B 2
C F 1
D A 4
D E 8
D F 1
F E 5
*/2.弗洛伊德演算法(Floyd)
關鍵方程為 lowcost[i][j] = min(lowcost[i][j], lowcost[i][k] + lowcost[k][j]);(初始化時lowcost[i][j] = G.arcs[i][j])
#include <bits/stdc++.h>
using namespace std;
#define MaxInt 32768
#define MVNum 100
typedef char VerTexType ;
typedef int ArcType;
typedef struct
{
VerTexType vexs[MVNum];
ArcType arcs[MVNum][MVNum];
int vexnum, arcnum;
}AMGraph;
int LocateVex(AMGraph G, VerTexType v)
{
for(int i = 0; i < G.vexnum; i ++)
{
if(G.vexs[i] == v)return i;
}
}
//建立無向帶權圖
void CreateUDN(AMGraph &G)
{
cout<<"輸入頂和邊的數目:"<<endl;
cin>>G.vexnum>>G.arcnum;
for(int i = 0; i < G.vexnum; i ++)cin>>G.vexs[i];
for(int i = 0; i < G.vexnum; i ++)
{
for(int j = 0; j < G.vexnum; j ++)
{
G.arcs[i][j] = MaxInt;
}
}
VerTexType u, v;
ArcType w;
for(int i = 0; i < G.arcnum; i ++)
{
cin>>u>>v>>w;
int uid = LocateVex(G, u), vid = LocateVex(G, v);
G.arcs[uid][vid] = G.arcs[vid][uid] = w;
}
}
void Floyd(AMGraph G)
{
ArcType lowcost[MVNum][MVNum];
for(int i = 0; i < G.vexnum; i ++)
{
for(int j = 0; j < G.vexnum; j ++)
{
lowcost[i][j] = G.arcs[i][j];
}
}
for(int k = 0; k < G.vexnum; k ++)
{
for(int i = 0; i < G.vexnum; i ++)
{
for(int j = 0; j < G.vexnum; j ++)
{
lowcost[i][j] = min(lowcost[i][j], lowcost[i][k] + lowcost[k][j]);
}
}
}
for(int i = 0 ; i < G.vexnum; i ++)
{
for(int j = 0; j < G.vexnum; j ++)
{
cout<<lowcost[i][j]<<" ";
}
cout<<endl;
}
}
int main()
{
AMGraph G;
CreateUDN(G);
Floyd(G);
return 0;
}
/*
6 8
A B C D E F
A B 3
B E 7
C B 2
C F 1
D A 4
D E 8
D F 1
F E 5
*/
3.演算法分析:
Dijkstra演算法的複雜度為O(n^2),Floyd演算法的複雜度為O(n^3)
Dijkstra演算法只能求一點到其他點的最短路徑,Floyd演算法能求任意兩點的最短路徑
(3)拓撲排序
拓撲排序:將AOV-網(Activity On Vertex Network)中所有頂點排成一個線性序列,該線性序列滿足:若在AOV-網中由頂點vi到頂點vj有一條路徑,則在該線性序列中的頂點vi必在頂點vj之前。(前提:AOV-網不能出現有向環)
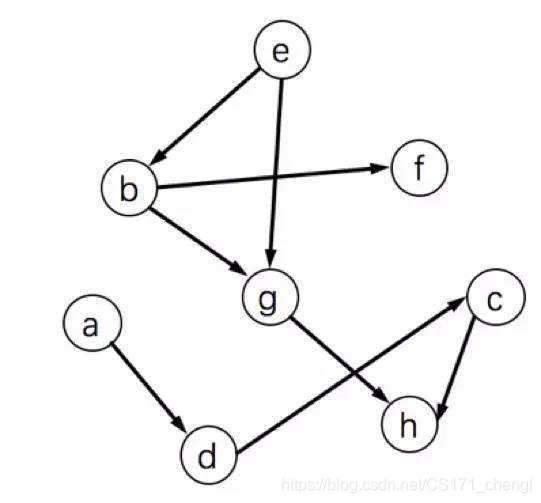
其拓撲序列可以為 e b g f a d c h
程式碼實現:(棧實現)
/*
使用鄰接表儲存的有向圖
為方便起見,,使用C++STL中整合的棧stack
*/
#include <bits/stdc++.h>
using namespace std;
#define MaxInt 32768
#define MVNum 100
typedef char VerTexType; //節點的資料型別
typedef int ArcType;
int indegree[MVNum];
typedef struct ArcNode //定義節點
{
int adjvex; //指向下一個節點的位置
struct ArcNode *nextarc; //指向下一個節點
}ArcNode;
typedef struct VNode //定義每一個頂點
{
VerTexType data; //頂點表示的值
ArcNode *firstarc; //指向第一條依附於該頂點的邊的指標
}VNode, AdjList[MVNum]; //鄰接表
typedef struct //定義圖
{
AdjList vertices; //圖的頂點
int vexnum, arcnum; //圖的頂點數、邊數
}ALGraph;
int LocateVex(ALGraph G, VerTexType v)
{
for(int i = 0; i < G.vexnum; i ++)
if(v == G.vertices[i].data)return i;
}
//建立有向圖(無環)
void CreateDN(ALGraph &G)
{
ArcNode *p;
cout<<"請輸入頂點和邊的數目:"<<endl;
cin>>G.vexnum>>G.arcnum;
cout<<"請輸入頂點:"<<endl;
for(int i = 0; i < G.vexnum; i ++)
{
cin>>G.vertices[i].data;
G.vertices[i].firstarc = NULL;
}
for(int i = 0; i < G.vexnum; i ++)indegree[i] = 0;
VerTexType u, v;
cout<<"請輸入邊:"<<endl;
int uid, vid;
for(int i = 0; i < G.arcnum; i ++)
{
cin>>u>>v;
uid = LocateVex(G, u); vid = LocateVex(G, v);
p = new ArcNode;
indegree[vid] ++;
p->adjvex = vid;
p->nextarc = G.vertices[uid].firstarc; G.vertices[uid].firstarc = p;
}
}
stack<int>st;
void TopoSort(ALGraph G)
{
VerTexType topo[MVNum];
for(int i = 0; i < G.vexnum; i ++)
{
if(!indegree[i])st.push(i); //入度為零的頂點入棧
}
int m = 0; //記錄頂點的個數
while(!st.empty())
{
int v = st.top(); st.pop(); //將棧頂頂點彈出
topo[m++] = G.vertices[v].data;
ArcNode *p;
p = G.vertices[v].firstarc;
while(p)
{
//將與頂點p鄰接點頂點的入度減一
int k = p->adjvex;
indegree[k]--;
if(!indegree[k]) st.push(k); //入度為零的頂點入棧
p = p->nextarc;
}
}
if(m < G.vexnum) {cout<<"存在有向環"<<endl;return;}
for(int i = 0; i < G.vexnum; i ++)cout<<topo[i]<<" ";
cout<<endl<<endl;
}
int main()
{
ALGraph G;
CreateDN(G);
TopoSort(G);
return 0;
}
/*
8 8
a b c d e f g h
a d
d c
c h
e b
b g
g h
b f
e g
*/
