噪聲筆記#4 梯度噪聲_Simplex Noise
柏林噪聲很好用,但是它計算需要的頂點數是,隨著維度的增加,需要的頂點數急劇上升。於是在2001 年的 Siggraph上,他展示了 “simplex noise”,它比perlin有更低的計算量和優化。
Simplex是單形的意思
通俗解釋單形的話,可以認為是在N維空間裡,選出一個最簡單最緊湊的多邊形,讓它可以平鋪整個N維空間。我們可以很容易地想到一維空間下的單形是等長的線段(1-單形),把這些線段收尾相連即可鋪滿整個一維空間。在二維空間下,單形是三角形(2-單形),我們可以把等腰三角形連線起來鋪滿整個平面。三維空間下的單形,即3-單形就是四面體。更高維空間的單形也是存在的。
總之記住構成單形的定點數是n+1就行了,所以3維只要4個點,4維只要5個點,和perlin噪聲相比分別省了5個點和11個點,維度越高優勢越大。
另外n!個單形可以構成一個超晶格體,也就是perlin噪聲中用到的晶格,在simplex噪聲中單形轉化成超晶格會用到,比如在2d中,2個(2!)單形構成一個晶格,在3d中則需要6個(3!)。
看起來只是單純的換個取點的晶格,但理解起來真的腦闊疼,我以2D的simplex noise為例,把這個過程一步步分開。
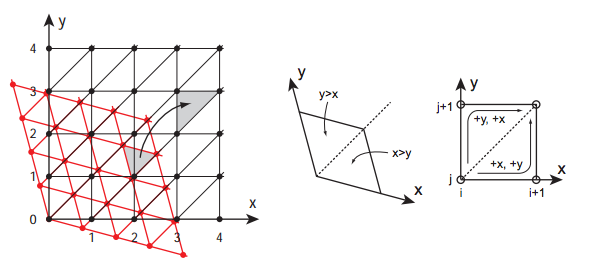
一、 通過偏斜(Skewing)把單形晶格轉換成容易計算的正晶格
就像這張圖一樣,注意是從紅色的單形轉換成黑色的正方形網格。轉換公式如下:
本來想看這個公式怎麼推出來的,結果我找了半天只找到偏斜座標 https://en.wikipedia.org/wiki/Skew_coordinates 然後我被勸退了,也不知道是不是同一個意思 。。。。
float F=0.366025404 // (sqrt(3)-1)/2 float2 SkewPos = p + (p.x + p.y) * F; float2 Skewi=floor(SkewPos); float2 Skewf=frac(SkewPos); /* PS:在這裡我遇到了一個誤區, 我以為i和Skewi;f和Skewf是對應的,後面就混著用了。但實際上,只有p和SkewPos是對應的 因為floor和frac都是基於1的計算,但是偏斜座標裡的1和正常座標裡的1不是同一單位!!!! 雖然我覺得這個錯誤很蠢,但我還是記錄一下,所以這裡標了出來,在實際運用中,我們只會用到Skewi和skewf。 i和f是沒有意義的 */ float2 i=floor(p); float2 f=frac(p);
二、找到正晶格中對應的單形晶格
也就是找到該畫素點插值所需要的n+1個頂點。一個正晶格中有n!個單形晶格,在2D中,一個正晶格由2個單形晶格組成。
怎麼找呢?
比如畫素點的f向量是(x,y,...),我們把f向量的各個值從大到小排序,然後先從(0,...0)開始,然後是維度中最大的值,比如說y最大,那麼就把y值設為1,第二個頂點,就是(0,1,...,0),x第二大,那麼第二個頂點的基礎上把x的維度設為1.依次推類得到n+1個頂點。
我的理解就是一點點縮小範圍,最後得到確定的單形,
以3D為例,如果畫素點的位置是(0.2,0.4,0.3)
第一個頂點是(0,0,0),此時6個單形都可能是目標單形,換句話說 xyz的大小排列組合有6種
y軸部分的值最大,所以第二個頂點為(0,1,0),剔除了x>y>z;x>z>y;z>y>x;z>x>y這4個晶格,因為這些晶格是不可能包括(0,1,0)這個頂點的,也不可能包含畫素點。
z軸部分第二大,所以第三個頂點為(0,1,1),剔除了y>x>z的情況,這時候晶格已經確定了。
最後一個頂點(1,1,1)收尾
就像正晶格中的單形晶格的數量是n!=n*(n-1)..*2*1一樣,一開始有n!個,確定一個點後還剩是(n-1)!個,不停的確定點,最後只剩下1!個。
2D確認單形的程式碼塊如下
float2 p0=float2(0,0);
float2 p1 = (Skewf.x < Skewf.y) ? float2(0.0, 1.0) : float2(1.0, 0.0);
float2 p2=float2(1,1);三、根據頂點得到梯度向量
這步和perlin噪聲一樣,以permutation排列表為索引得到頂點梯度向量,當然我又偷懶了,直接隨機取值吧
float2 grad1=hash2(p0+Skewi);
float2 grad2=hash2(p1+Skewi);
float2 grad3=hash2(p2+Skewi);四、得到畫素點和頂點的距離向量
計算距離時我們要求的是,未偏斜前的頂點和畫素點的距離,所以要先把偏斜頂點位置轉換成原位置,這裡就需要用到前面的偏斜公式F的逆函式:
但是像o1=p1-(p1.x+p1.y)*G這樣得到每個頂點位置然後再求距離比較麻煩(後面兩個頂點要先加再算),所以我們用只算一個然後推導另外兩個。
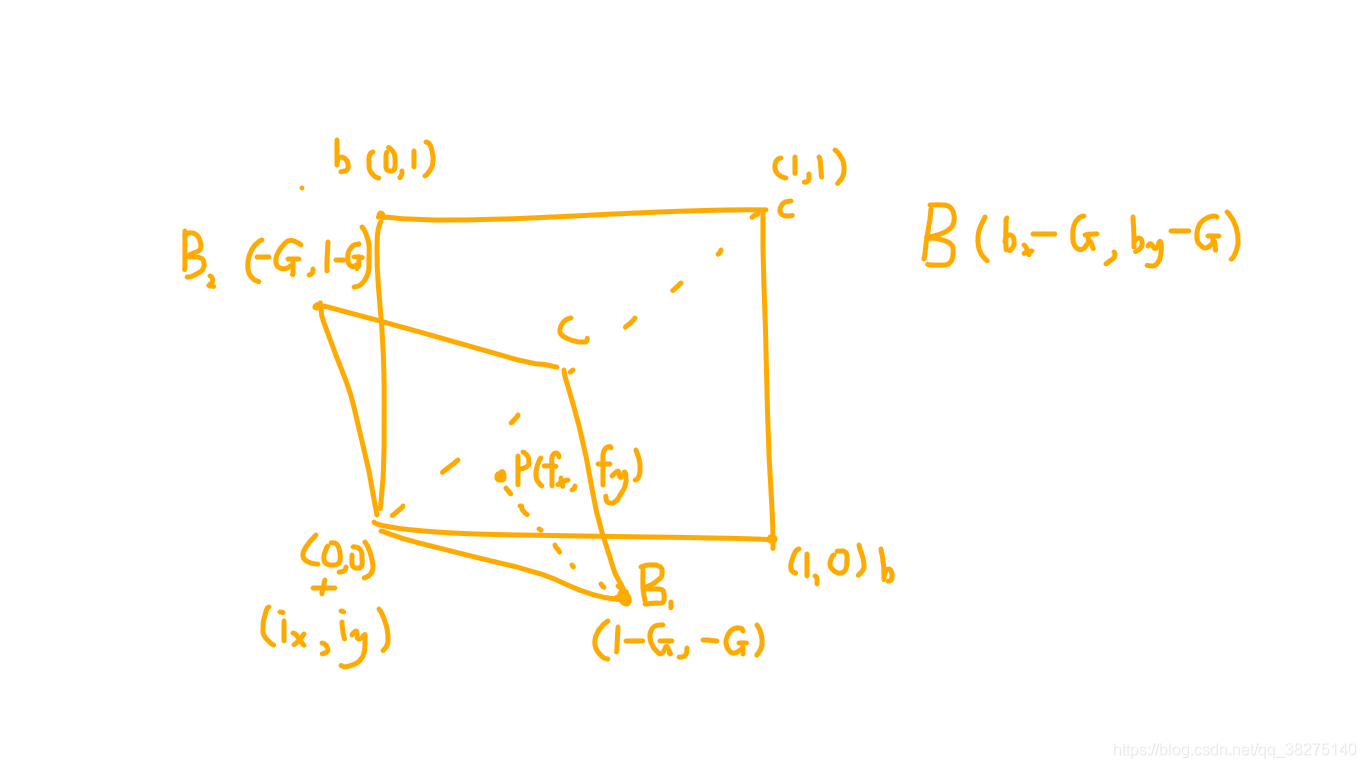
首先為了方便計算,我們把A點偏移到原點,因為距離是這幾點之間的相對關係,所以不會受影響,b點共有兩種情況,所以用(bx-G,by-G)來同一表示B點,同時我們的畫素點P為(fx,fy),f就是先前求的座標的小數部分,P同時也表示和第一個點(0,0)的距離,最後是C(1-2G,1-2G);
點都有了接下來開始求距離
OK,帶入就行了,3D思路一樣
float G = 0.211324865; // (3-sqrt(3))/6;
float2 d1=p - (Skewi - (Skewi.x + Skewi.y) * G);
float2 d2=d1-p1+G;
float2 d3=d1-1+2*G;五、插值求和
處理之前講的插值的Hermite函式3次變四次之外,由於是單形了,所以權值的計算肯定不能像perlin一樣,直接用f值了。
Simplex利用求和替代了Perlin噪聲的插值,使用一個精.心選擇的徑向衰減函式對每個頂點的貢獻值進行計算然後求和,計算頂點貢獻值的函式如下:
dist是距離向量,grad是梯度向量,r^的取值一般是0.5 ,因為dist^2最大為0.5(所以如果確認用0.5 max()感覺可以不用),但設為0.6是效果可能會更好。
//h=r^2-dist^2
float3 h = max(0.5 - float3(dot(d1, d1), dot(d2, d2), dot(d3, d3)), 0.0);
float3 n = h * h * h * h * float3(dot(d1, grad1), dot(d2, grad2), dot(d3, grad3));
//=>70*(n.x+n.y+n.z)
return dot(float3(70,70,70),n);//這裡返回的是(-1,1),用於顏色值要對映成(0,1)
兩個補充:
1、dist^2為啥最大為0.5: 距離最大就是點到對邊(面)的距離,也就是高,正三角形高是邊的倍,轉化後的正方形邊長為1,可以得到原來正三角形的邊長為
【算(1,1)頂點對應的原位置即可得到】相乘高為
,平方即為0.5.
2、為啥最後要乘70:因為我們必須把返回值的範圍控制在[-1,1]之間,而算出來的絕對值最大卻不是1,而當點在每一條邊的中點時,值最大,前面我們已經知道了邊長和高,隨便算一下,就知道三個距離為(,
,
),當r^2=0.5時,h=(0,
,
),梯度向量和距離向量點乘部分想要最大,方向相同 cos=1,相反-1(這也是為什麼範圍是(-1,1)而不是(0,1)的原因)兩個向量模最大的時候,距離向量前面已經確定是,而梯度向量模最大為
。
PS:關於梯度模的最大值,這裡是因為隨機取值,所以(1,1)最大,為 ,如果按照標準的預設梯度向量,模應該都是一,我看到一篇文章它用的預設梯度向量的方法,但最終還是乘以70,最後我發現它取梯度向量時,是用的3d梯度向量中的前兩個值xy,
http://staffwww.itn.liu.se/~stegu/simplexnoise/simplexnoise.pdf
double t0 = 0.5 - x0*x0-y0*y0;
if(t0<0) n0 = 0.0; else { t0 *= t0; n0 = t0 * t0 * dot(grad3[gi0], x0, y0);
// (x,y) of grad3 used for 2D gradient }
所以乘最終值時,還是應該考慮到具體取值的的情況
分別計算並相加三個值,所以最後的最大值:
這是r^2=0.5的時候,如果r^2=0.6,應該乘24.5左右。如果3D的話,邊長 ,0.5,最後應該乘31.32。
2D Simplex噪聲

Shader "Custom/SimplexNoise2D" {
Properties{
_Scale("Scale",Range(3,50)) = 10
}
SubShader{
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#pragma vertex vert
#pragma fragment frag
#define F 0.366025404
#define G 0.211324865
float _Scale;
struct v2f {
float4 pos:SV_POSITION;
half2 uv:TEXCOORD0;
};
v2f vert(appdata_base v) {
v2f o;
o.pos = UnityObjectToClipPos(v.vertex);
o.uv = v.texcoord;
return o;
}
float2 random(float2 p) {
p = float2(dot(p, float2(127.1, 311.7)),
dot(p, float2(269.5, 183.3)));
return -1.0 + 2.0 * frac(sin(p)*43758.5453123);
}
float simplexNoise(float2 p) {
float2 SkewPos = p + (p.x + p.y) * F;
float2 Skewi = floor(SkewPos);
float2 Skewf = frac(SkewPos);
float2 p1 = (Skewf.x < Skewf.y) ? float2(0.0, 1.0) : float2(1.0, 0.0);
float2 d1 = p - (Skewi - (Skewi.x + Skewi.y) * G);
float2 d2 = d1 - p1 + G;
float2 d3 = d1 - 1 + 2 * G;
float3 h = max(0.5 - float3(dot(d1, d1), dot(d2, d2), dot(d3, d3)), 0.0);
float3 n = h * h * h * h * float3(dot(d1, random(Skewi)), dot(d2, random(Skewi + p1)), dot(d3, random(Skewi + 1)));
return dot(float3(70, 70, 70), n);
}
fixed4 frag(v2f i) :SV_Target{
float noise = (simplexNoise(i.uv*_Scale)+1)*.5;
return float4(noise, noise, noise, 1);
}
ENDCG
}
}
FallBack "Diffuse"
}
3D Simplex噪聲

Shader "Custom/SimplexNoise3D" {
Properties{
_Scale("Scale",Range(3,50)) = 10
}
SubShader{
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#pragma vertex vert
#pragma fragment frag
//注意這裡,這裡一定要用小數,不要直接1/3 1/6 會出錯的,害我檢查半天!
#define F 1.0/3.0
#define G 1.0/6.0
float _Scale;
struct v2f {
float4 pos:SV_POSITION;
half2 uv:TEXCOORD0;
};
v2f vert(appdata_base v) {
v2f o;
o.pos = UnityObjectToClipPos(v.vertex);
o.uv = v.texcoord;
return o;
}
float3 random(float3 p) {
p = float3(dot(p, float3(127.1, 311.7, 74.7)),
dot(p, float3(269.5, 183.3, 246.1)),
dot(p, float3(113.5, 271.9, 124.6)));
return -1.0 + 2.0 * frac(sin(p)*43.5453123);
}
float simplexNoise(float3 p) {
float3 SkewPos = p + (p.x + p.y+p.z) * F;
float3 Skewi = floor(SkewPos);
float3 Skewf = frac(SkewPos);
float3 p1;
float3 p2;
/*if (Skewf.x>Skewf.y) {
if (Skewf.y > Skewf.z) {//xyz
p1 = float3(1, 0, 0);
p2 = float3(1, 1, 0);
}
else if (Skewf.x > Skewf.z) {//xzy
p1 = float3(1, 0, 0);
p2 = float3(1, 0, 1);
}
else {//zxy
p1 = float3(0, 0, 1);
p2 = float3(1, 0, 1);
}
}
else {//y>x
if (Skewf.y < Skewf.z) {//zyx
p1 = float3(0, 0, 1);
p2 = float3(0, 1, 1);
}
else if (Skewf.x<Skewf.z){//yzx
p1 = float3(0, 1, 0);
p2 = float3(0, 1, 1);
}
else {//yxz
p1 = float3(0, 1, 0);
p2 = float3(1, 1, 0);
}
}*/
//這裡我用step代替if,計算量可能會小點
float xy = step(Skewf.y , Skewf.x);//等價於(x>y)?1:0
float xz = step(Skewf.z , Skewf.x);
float yx = step(Skewf.x , Skewf.y);
float yz = step(Skewf.z , Skewf.y);
float zx = step(Skewf.x , Skewf.z);
float zy = step(Skewf.y , Skewf.z);
//相乘只有最大數的結果才是1;
p1 = float3(xy*xz,yx*yz,zx*zy);
//相加結果是210,減去p1的100 結果就是110
p2 = float3(xy+xz, yx+yz, zx+zy)-p1;
float3 d1 = p - (Skewi - (Skewi.x + Skewi.y+ Skewi.z) * G);
float3 d2 = d1 - p1 + G;
float3 d3 = d1 - p2 + 2 * G;
float3 d4 = d1 - 1 + 3 * G;
float4 h = max(0.6 - float4(dot(d1, d1), dot(d2, d2), dot(d3, d3), dot(d4, d4)), 0.0);
float4 n = h * h * h * h * float4(dot(d1, random(Skewi)), dot(d2, random(Skewi + p1)), dot(d3, random(Skewi + p2)), dot(d4, random(Skewi + 1)));
return 32*(n.x+n.y+n.z+n.w);
}
fixed4 frag(v2f i) :SV_Target{
float3 pos = float3(i.uv.xy*_Scale,_Time.y);
float noise = (simplexNoise(pos) + 1)*.5;
return float4(noise, noise, noise, 1);
}
ENDCG
}
}
FallBack "Diffuse"
}
參考內容:http://staffwww.itn.liu.se/~stegu/simplexnoise/simplexnoise.pdf