噪聲筆記#5 Worley噪聲
Worley noise也叫Voronoi/Cellular noise,叫Voronoi是因為基於Voronoi 演算法,Voronoi圖,叫Worley是因為1996年Steven Worley 寫了一篇名為“A Cellular Texture Basis Function”的論文。在這篇論文裡,他描述了這種現在被廣泛使用的程式化紋理技術。
worely噪聲有別與前面幾種噪聲,它是隨機生成幾個特徵點,然後每個畫素點的取值是它與最近特徵點之間的距離。
比如你有四個特徵點,
float2 Rpoints[4]; Rpoints[0] = float2(0.83, 0.75); Rpoints[1] = float2(0.60, 0.07); Rpoints[2] = float2(0.28, 0.64); Rpoints[3] = float2(0.31, 0.26); float m_dist = 1; for (int i = 0; i < 4;i++) { m_dist=min(m_dist, distance(uv, Rpoints[i])); }

但這樣有個問題,如果你生成的特徵點少還好,如果需要生成大量特徵點,越多計算複雜度越大, 而且這些特徵點你要提前準備好,不然每個特徵點都要重新計算一遍。所以Steven Worley對此進化了優化。把空間分割成網格,每個格子生成一個特徵點,畫素點只在自己和周圍八個網格里尋找最近的特徵點距離。這樣無論最終有多少個特徵點,每個畫素只會迴圈算9次最短距離
for (int x = -1; x < 2;x++) { for (int y = -1; y < 2; y++) { float2 neighbor = float2(x, y); //自己和周圍網格的特徵點 float2 neighborP = random(i + neighbor) ; //距離 float dist = distance(f,neighborP+ neighbor); m_dist = min(m_dist, dist); } }

如圖,每個網格里都有一個特徵點,仔細看可以發現,每一個cell邊不會超過8條,因為它只是在周圍8點尋找最近距離。
3x3 Worley噪聲
前面直接把最小值作為返回值使用了,當實際上求最小距離是為了得到最近特徵點,我們可以根據特徵點,返回一些別的值,這裡我用point的xy值來中和三個預設顏色,並在計算特徵點時加了動態。

Shader "Custom/WorleyNoise2D" { Properties{ _Scale("Scale",Range(5,50)) = 5 } SubShader{ Pass{ CGPROGRAM #include "UnityCG.cginc" #pragma vertex vert #pragma fragment frag float _Scale; struct v2f { float4 pos:SV_POSITION; half2 uv:TEXCOORD0; }; v2f vert(appdata_base v) { v2f o; o.pos = UnityObjectToClipPos(v.vertex); o.uv = v.texcoord; return o; } float2 random(float2 p) { p = float2(dot(p, float2(127.1, 311.7)), dot(p, float2(269.5, 183.3))); return frac(sin(p)*43758.5453123); } float3 worleyNoise(float2 uv) { float2 i = floor(uv); float2 f = frac(uv); float m_dist =1; float2 m_point; for (int x = -1; x < 2;x++) { for (int y = -1; y < 2; y++) { float2 neighbor = float2(x, y); //周圍的特徵點 float2 neighborP = random(i + neighbor) ; //動態 neighborP = 0.5 + 0.5*cos(_Time.y + 6.2831*neighborP); float dist = distance(f,neighborP+ neighbor); if (dist<m_dist) { //最短距離 m_dist = dist; //最近的特徵點 m_point = neighborP; } } } float3 color1 =float3(0.790, 0.320, 0.190); float3 color2 =float3(0.393, 0.790, 0.428); float3 color3 = float3(0.360, 0.644, 0.790); float3 color = lerp(color1, color2,m_point.x); color = lerp(color, color3, m_point.y); return color; } fixed4 frag(v2f i) :SV_Target{ float3 noise = worleyNoise(i.uv*_Scale); return fixed4(noise, 1); } ENDCG } } FallBack "Diffuse" }
2x2 Worley噪聲
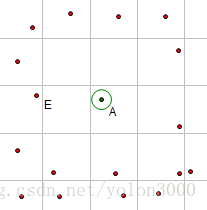
在 2011 年, Stefan Gustavson 優化了 Steven Worley 的演算法,僅僅對一個 2x2 的矩陣作遍歷(而不是 3x3 的矩陣)。這顯著地減少了工作量,但是會在網格邊緣製造人工痕跡。事實上這個問題在3x3上也存在,只是不明顯。
比如在上圖的情況下,離a點最近的點是e點,但是a點不在周圍的8個網格內,所以計算時不會計算E點和A點的距離,得到的自然不是真正的特殊點,這樣影象邊緣就會有割裂的感覺,好在3x3是這種情況很少,但是如果特徵點搜尋框變成了2x2,那麼就有可能出現明顯的效果。所以要在效果和效率之間做出選擇。
可以發現,特徵點越靠近網格中心,那麼出現割裂的可能性越低,所以在2x2的Worley噪聲中,特徵點的計算變為基於中心的一定強度的偏移擾亂,這樣可以避免極端情況出現。

Shader "Custom/2x2WorleyNoise2D" {
Properties {
_Scale("Scale",Range(3,50)) = 10
_Jitter("Jitter",Range(0,2)) = 0.5
}
SubShader{
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#pragma vertex vert
#pragma fragment frag
float _Scale;
float _Jitter;
struct v2f {
float4 pos:SV_POSITION;
half2 uv:TEXCOORD0;
};
v2f vert(appdata_base v) {
v2f o;
o.pos = UnityObjectToClipPos(v.vertex);
o.uv = v.texcoord;
return o;
}
float2 random(float2 p) {
p = float2(dot(p, float2(127.1, 311.7)),
dot(p, float2(269.5, 183.3)));
return frac(sin(p)*43758.5453123);
}
float worleyNoise(float2 uv) {
float2 i = floor(uv);
float2 f = frac(uv);
float m_dist = 1;
//四個特徵點,未進行擾亂前是四個網格中心
float2 originPoint = float2(0.5, 0.5);
float2 upPoint = float2(1.5, 0.5);
float2 rightPoint = float2(0.5, 1.5);
float2 urightPoint = float2(1.5, 1.5);
//新增擾亂,因為是計算右上的四個網格,所以擾亂應該向左下(-)擾亂,這樣才能避免出錯
originPoint -= random(i)*0.5*_Jitter;
upPoint -= random(i+float2(1,0))*0.5*_Jitter;
rightPoint -= random(i + float2(0,1))*0.5*_Jitter;
urightPoint -= random(i + float2(1,1))*0.5*_Jitter;
//算距離
float4 dis = float4(distance(f, originPoint), distance(f, upPoint), distance(f, rightPoint), distance(f, urightPoint));
m_dist = min(min(dis.x, dis.y), min(dis.z, dis.w));
return m_dist;
}
fixed4 frag(v2f i) :SV_Target{
float v =worleyNoise(i.uv*_Scale);
v = 1-1.5*worleyNoise(i.uv*_Scale);
return fixed4(v, v, v, 1);
}
ENDCG
}
}
FallBack "Diffuse"
}
Worley 噪聲的邊緣
前面的Worley噪聲是的最小距離時基於歐幾里得演算法,所以他的距離漸變是一個圓形,但是有時候我們可能希望他的距離時按照多邊形邊緣漸變,
我們可以通過F2-F1得到一個近似的效果(F1是最短距離,F2是第二短距離);

但是效果不是很好,Inigo Quile在2012年寫了一篇有關Voronoi borders的文章,講了一個實現方法。

如圖所示,x是畫素點位置 a是離x最近的特徵點,b是第二近的特徵點,m是兩者的中點,也是在兩個cell的接觸線上,紫色的線長度就是離邊緣線的距離,等於在
上的投影 即:
至於尋找第二近特徵點,你可以在原本的9個特徵點離直接找,但效果不好,這裡是在基於最近特徵點(不是畫素點所在網格的特徵點)的5x5搜尋框裡尋找



Shader "Custom/3x3WorleyNoiseBorder" {
Properties{
_Scale("Scale",Range(5,50)) = 5
}
SubShader{
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#pragma vertex vert
#pragma fragment frag
float _Scale;
struct v2f {
float4 pos:SV_POSITION;
half2 uv:TEXCOORD0;
};
v2f vert(appdata_base v) {
v2f o;
o.pos = UnityObjectToClipPos(v.vertex);
o.uv = v.texcoord;
return o;
}
float2 random(float2 p) {
p = float2(dot(p, float2(127.1, 311.7)),
dot(p, float2(269.5, 183.3)));
return frac(sin(p)*43758.5453123);
}
float worleyNoise(float2 uv) {
float2 i = floor(uv);
float2 f = frac(uv);
float m_dist = 8;
float2 mp;
float2 mr;
//正常的求最短距離
for (int x = -1; x < 2; x++)
for (int y = -1; y < 2; y++) {
float2 neighbor = float2(x, y);
float2 neighborP = random(i + neighbor);
float dist = distance(f, neighborP + neighbor);
if (dist < m_dist.x) {
//最短距離
m_dist.x = dist;
//最近的特徵點網格,下面要用
mp=neighbor;
//最近點和畫素點的距離向量,下面要用
mr = neighborP + neighbor - f;
}
}
//求邊緣距離 尋找(距離(最近特徵點)最近的特徵點) 5x5
float borderDis = 8;
for (int x = -2; x < 3; x++)
for (int y = -2; y < 3; y++) {
float2 neighbor = float2(x, y);
//mr=最近點和畫素點距離,r=第二近和畫素點距離,mr+r=2mx r-mr=ab
float2 neighborP = random(i+mp + neighbor);
float2 r = mp + neighborP + neighbor - f;
if (dot(mr - r, mr - r) > 0.00001) {//排除xy=0的情況
borderDis = min(borderDis, dot(0.5*(mr + r), normalize(r - mr)));
}
}
return borderDis;
}
fixed4 frag(v2f i) :SV_Target{
float n = worleyNoise(i.uv*_Scale);
float3 noise = n;//1
noise = 1.0 - smoothstep(0.0, 0.05, n);//2
noise = (0.5 + .5*cos(n*64))*n;//3
return fixed4(noise, 1);
}
ENDCG
}
}
FallBack "Diffuse"
}
Voronoise
Inigo 在 Voronoi 上的實驗並沒有就此停止。2014 年,他寫了一篇非常漂亮的文章,提出一種他稱作為 voro-noise 的噪聲,可以讓常規噪聲和 voronoi 逐漸地融合。
首先常規的噪聲是連續的,但Voronoi 噪聲不是連續的(邊界),所以想要結合,必需讓Voronoi 噪聲變成連續的,Inigo提出了一種smooth voronoi,讓voronoi變成連續的。總的來說,就是把原本的求最小值變成的各個特徵點距離之間的加權取值,
res += 1.0/pow( d, 8.0 );
...
return pow( 1.0/res, 1.0/16.0 )這是其中一種,文中給出了兩種,d是距離的平方,距離越小,加權加的值就越多。8次方意味著最大的數佔據了加權中的絕大部分。所以效果其實和正常的差不多,而且還是連續的。 return後面的運算其實就是把d給還原出來。
pow( pow(d,8), 1.0/16.0 )= 因為這裡d是距離的平方,所以正好開個根號。
這裡是8次方,所以會有加權的效果,但如果是res+=pow(d,n ),n=1 那就是每個距離單純的相加,
float ww = pow( 1.0-smoothstep(0.0,1.414,sqrt(d)), 64.0 - 63.0*v );再看這個,v值範圍在[0,1],
v=0時,ww=pow(1.0-smoothstep(0.0,1.414,sqrt(d)),64); //Voronoi 噪聲
v=1時,ww=1.0-smoothstep(0.0,1.414,sqrt(d));//可以把值看成常規噪聲中每個網格的隨機值,
ps:smoothstep是為了讓距離在[0,1.414]裡對映成[0,1],超出部分返回1,避免負數之類的 1.414≈根號2
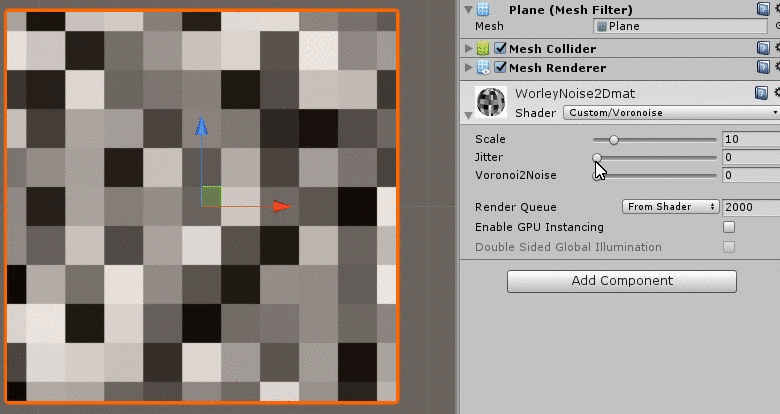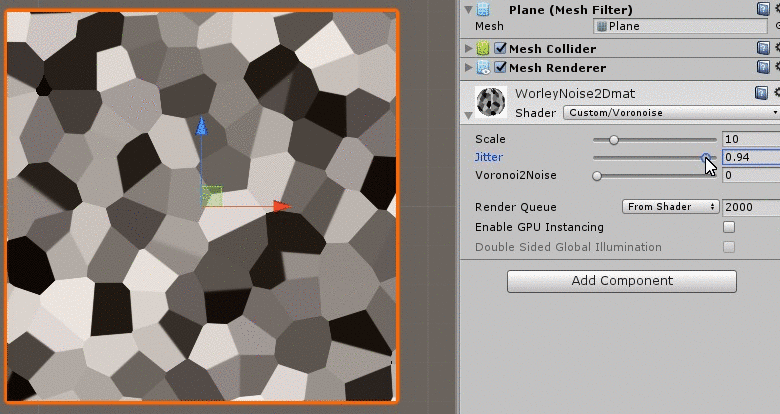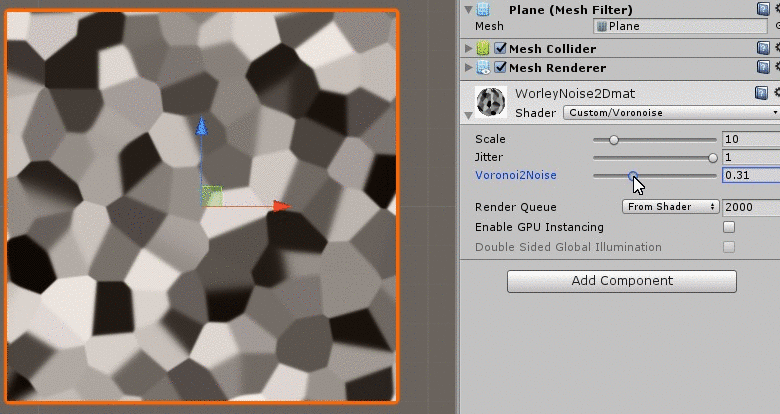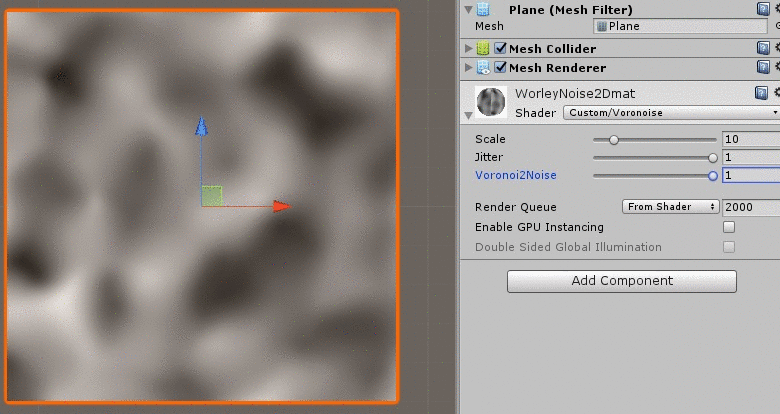
Shader "Custom/Voronoise" {
Properties{
_Scale("Scale",Range(3,50)) = 10
_Jitter("Jitter",Range(0,1)) = 0
_Lerp("Voronoi2Noise",Range(0,1)) = 0
}
SubShader{
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#pragma vertex vert
#pragma fragment frag
float _Scale;
float _Jitter;
float _Lerp;
struct v2f {
float4 pos:SV_POSITION;
half2 uv:TEXCOORD0;
};
v2f vert(appdata_base v) {
v2f o;
o.pos = UnityObjectToClipPos(v.vertex);
o.uv = v.texcoord;
return o;
}
float3 hash3(float2 p) {
float3 q = float3(dot(p, float2(127.1, 311.7)),
dot(p, float2(269.5, 183.3)),
dot(p, float2(419.2, 371.9)));
return frac(sin(q)*43758.5453);
}
float voronoise(float2 pos, float u, float v) {
float2 p = floor(pos);
float2 f = frac(pos);
float H = 1.0 + 63.0*pow(1.0 - v, 4.0);//這裡決定是像Voronoi還是noise
float vall = 0.0;
float wall = 0.0;
for (int j = -2; j < 3; j++) {
for (int k = -2; k <3; k++) {
float2 g = float2(k,j);
//前兩個隨機值用於特徵點的擾動
float3 o = hash3(p + g)*float3(u, u, 1.0);
float2 r = g-f+o.xy;//畫素點和特徵點距離向量
float d = dot(r, r);//距離^2
float ww = pow(1.0 - smoothstep(0.0, 1.414, sqrt(d)), H);
vall += o.z*ww;
wall += ww;
}
}
return vall / wall;//歸一化在(0,1)
}
fixed4 frag(v2f i) :SV_Target{
float3 noise = voronoise(i.uv*_Scale,_Jitter,_Lerp);
return fixed4(noise, 1);
}
ENDCG
}
}
FallBack "Diffuse"
}
參考內容 :https://blog.csdn.net/yolon3000/article/details/78386701