噪聲筆記#2 插值和值噪聲
白噪聲實在是太隨機了,隨機值之間沒什麼相關性,而在現實中,像波浪,葉脈紋理這些在隨機中又帶著規律性,因此想要模擬這些的噪聲(Noise)也需要在隨機中帶點相關性。
(1)用插值連線隨機點
之前實現白噪聲,每個畫素塊彼此完全獨立,隨機點之間沒有聯絡。想要把這些隨機點連線起來就需要插值。
這裡列幾個常用的插值方法 比如說有這樣幾個隨機點

第一種,線性插值 :,
float i = floor(x); float f = fract(x); y = mix(rand(i), rand(i + 1.0), f);//mix等價於rand(i+1.0)*f+rand(i)*(1.0-f);

第二種 餘弦插值:線上性插值的基礎上,把t值替換成一個餘弦值,這樣插值就會變得平滑
f*=3.1415926;//轉化為弧度制 [0,π]
f=(1.-cos(f))*0.5;//對映在[0,1]
y = mix(rand(i), rand(i + 1.0), f);
//y = mix(f1(floor(x)), f2(floor(x) + 1.0), (1-cos(frac(x)*3.1415))*0.5;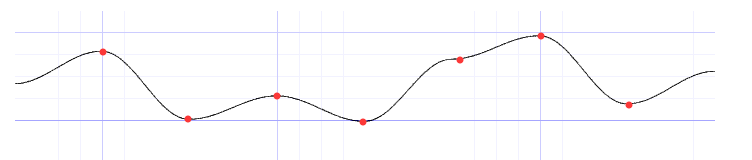
第三種 :Cubic 插值:利用三次方多項式來插值
PS:在找相關資料的時候發現還有一種叫三次樣條插值的(Cubic Spline Interpolation),這兩個應該是不一樣的,不要搞混
推導過程:
x帶入0,1
得
我們可以把f(0) f(1) 看做插值的前後兩個點p1,p2,f'(0),f'(1)則可以表示曲線在這兩個點上的導數,可以把它設為0,但是把它設為前後兩點的斜率,可以得到更平滑的曲線。( 如p1的前後兩個點p2和p0 )
帶入
得
float v0=rand(i-1.); float v1=rand(i); float v2=rand(i+1.); float v3=rand(i+2.); y=v1+f*(0.5*(v2-v0)+f*(0.5*(2.*v0-5.*v1+4.*v2-v3)+f*(0.5*(-v0+3.*v1-3.*v2+v3))));
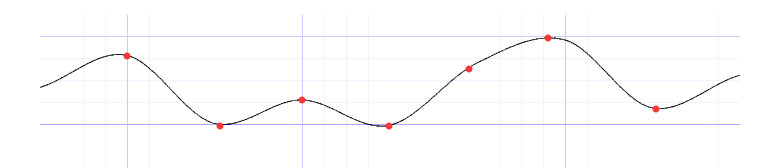
在第六個點可以看到和餘弦插值明顯的不同。
再PS:還找到一種Cubic 插值公式是:
但不知道是怎麼推出來的,試了一下,效果也可以,而且這式子看起來還簡單點。
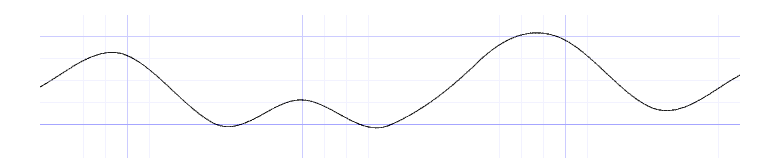
float v1=rand(i);
float v2=rand(i+1.);
float v3=rand(i+2.);
y=((v3-v2)-(v0-v1))*f*f*f+(2.*(v0-v1)-(v3-v2))*f*f+(v2-v0)*f+v1;第四種:Hermite插值:smoothstep();用的就是這種插值方法(優化過)
三次Hermite插值公式:
m0,m2表示v0,v2的方向(切向量),懶得管可以設為0;
TODO 沒懂它的原理,以後再來補吧
float u = f * f * (3.0 - 2.0 * f ); //-2f^3+3f^2
y = mix(rand(i), rand(i + 1.0), u);
//把這裡的mix()拆開就等於m1,m2=0的三次Hermite插值
//(2f^3-3f^2+1)*rand(i)+(-2*f^3+3*t^2)*rand(i+1);emmmmm 從這張圖看的話感覺和餘弦插值差不多嘛
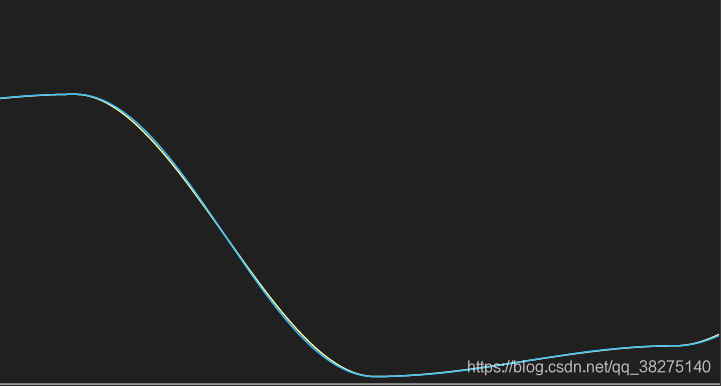
黃色三次hermite,藍色餘弦插值,本來想找點不同的。。。
(2) 2D值噪聲
回到正題,值噪聲之所以叫值噪聲(Value Noise),就是它是在隨機值(random value)之間插值得到的noise值,後面還會寫到梯度噪聲(Gradient Noise),就是用的別的方法得到noise值。
在一維插值是從兩個點中插值,轉變到二維,則是從四個點中插值
把平面想象成一塊塊的網格,一個網格由四個點構成,每個點都是一個固定的隨機值,每個畫素點都在某一個網格中,根據它對於四個點的相對位置,插值得到畫素點的隨機值(噪聲值)

如果把noise值想象成高度的話
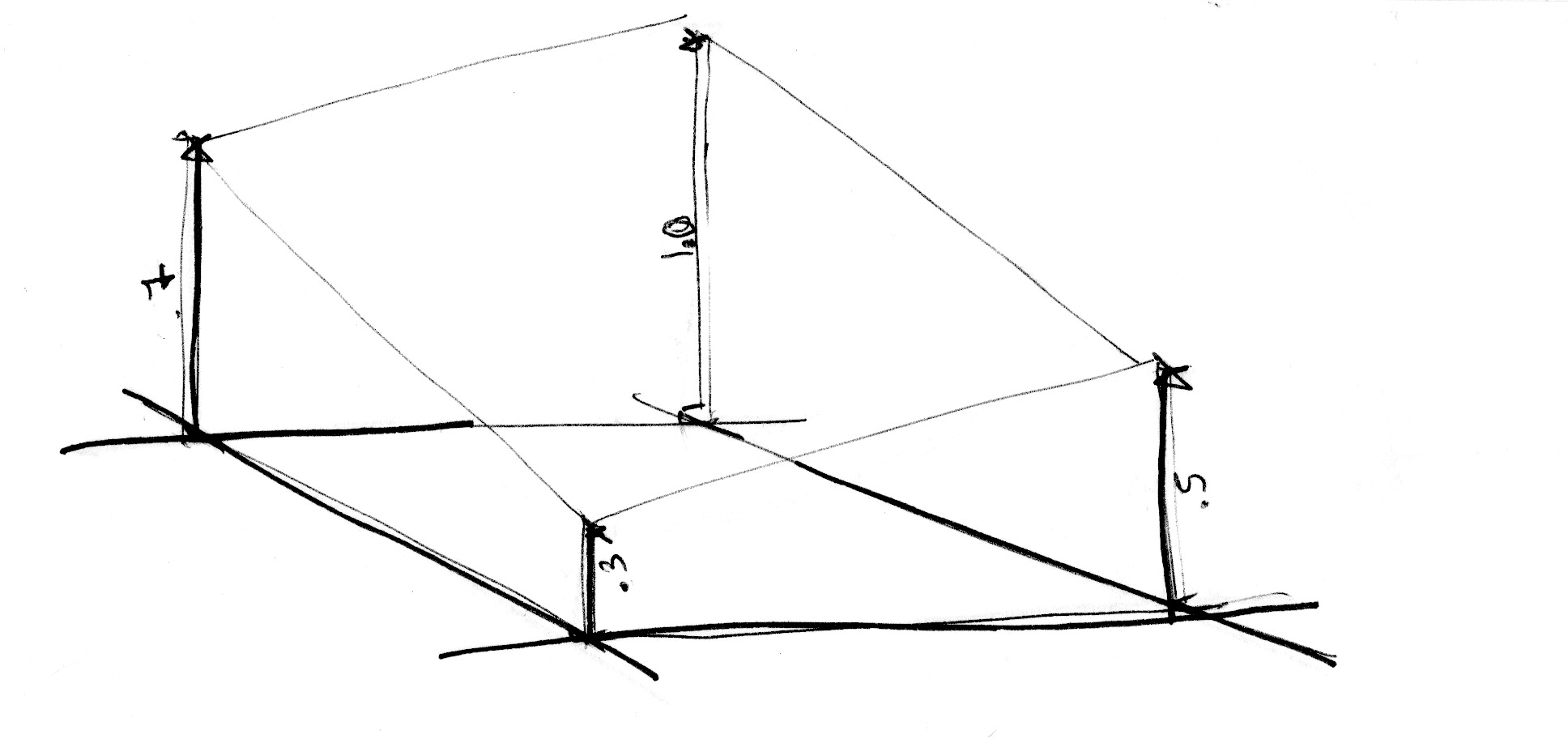
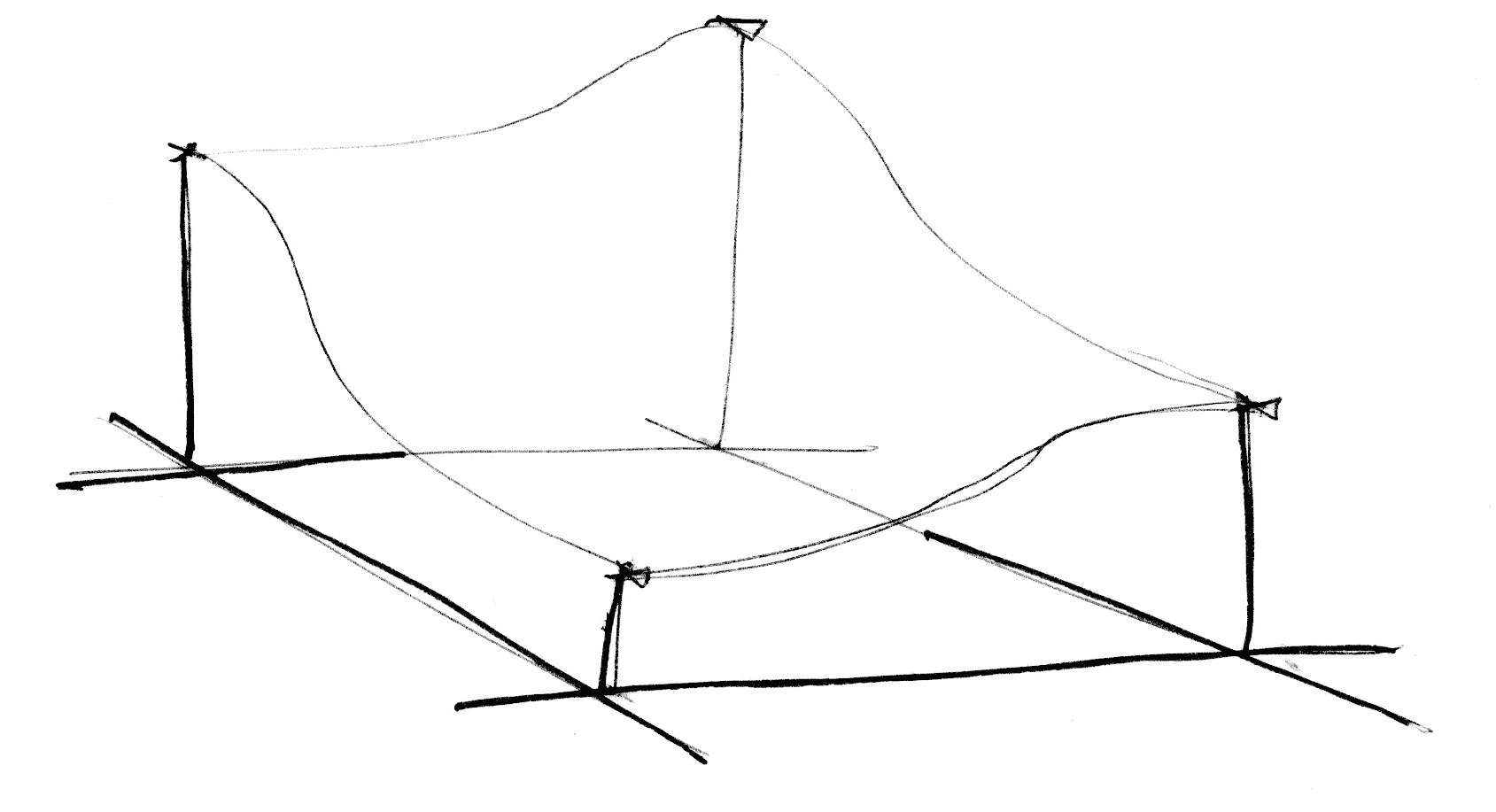
直接的線性插值 平滑插值
用unityshader繪製2D值噪聲

Shader "Custom/ValueNoise2D" {
Properties{
_Scale("Scale",Range(4,20)) = 10
}
SubShader{
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#pragma vertex vert
#pragma fragment frag
float _Scale;
struct v2f {
float4 pos:SV_POSITION;
half2 uv:TEXCOORD0;
};
v2f vert(appdata_base v) {
v2f o;
o.pos = UnityObjectToClipPos(v.vertex);
o.uv = v.texcoord;
return o;
}
float rand(float2 st) {
return frac(sin(dot(st.xy,
float2(12.9898, 78.233)))
* 43758.5453123);
}
float mix(float a, float b, float t) {
return b*t + a*(1 - t);
}
float ValueNoise(float2 uv) {
float2 i = floor(uv);
float2 f = frac(uv);
float a = rand(i);
float b = rand(i + float2(1, 0));
float c = rand(i + float2(0, 1));
float d = rand(i + float2(1, 1));
float2 u= f*f*(3.0 - 2.0*f);//三次Hermite插值
return mix(a, b, u.x) +
(c - a)* u.y * (1.0 - u.x) +
(d - b) * u.x * u.y;
}
fixed4 frag(v2f i) :SV_Target{
half2 uv = i.uv * _Scale;
float noise = ValueNoise(uv);
return fixed4(noise, noise, noise, 1);
}
ENDCG
}
}
FallBack "Diffuse"
}
四個點的插值公式一開始看有點懵逼,但其實就是把幾個mix()拆開了。
return mix(a, b, u.x) +(c - a)* u.y * (1.0 - u.x) +(d - b) * u.x * u.y;
return mix(mix(a, b, u.x), mix(c, d, u.x), u.y);//把這個拆開,就是上面的這個式子(2) 3D值噪聲
以此推類3D噪聲,也就是8個點的插值,這裡我把時間作為第三個變數,有一個動態的效果

Shader "Custom/ValueNoise3D" {
Properties{
_Scale("Scale",Range(4,20)) = 10
}
SubShader{
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#pragma vertex vert
#pragma fragment frag
float _Scale;
float _lerp;
struct v2f {
float4 pos:SV_POSITION;
half2 uv:TEXCOORD0;
};
v2f vert(appdata_base v) {
v2f o;
o.pos = UnityObjectToClipPos(v.vertex);
o.uv = v.texcoord;
return o;
}
float rand(float3 st) {
return frac(sin(dot(st.xyz,
float3(127.1, 311.7, 74.7)))
* 43758.5453123);
}
float mix(float a, float b, float t) {
return b*t + a*(1 - t);
}
float ValueNoise3D(float3 uvt) {
float3 i = floor(uvt);
float3 f = frac(uvt);
float a = rand(i);
float b = rand(i + float3(1, 0, 0));
float c = rand(i + float3(0, 1, 0));
float d = rand(i + float3(1, 1, 0));
float e = rand(i + float3(0, 0, 1));
float fx = rand(i + float3(1, 0, 1));
float g = rand(i + float3(0, 1, 1));
float h = rand(i + float3(1, 1, 1));
float3 u= f*f*(3.0 - 2.0*f);
float mix1 = mix(mix(a, b, u.x), mix(c, d, u.x), u.y);
float mix2 = mix(mix(e, fx, u.x), mix(g, h, u.x), u.y);
return mix(mix1, mix2, f.z);//這裡感覺用線性的f.z效果好點,也可以選擇平滑後的u.z
}
fixed4 frag(v2f i) :SV_Target{
half2 uv = i.uv * _Scale;
float noise = ValueNoise3D(float3(uv.xy,_Time.y));
return fixed4(noise, noise, noise, 1);
}
ENDCG
}
}
FallBack "Diffuse"
}
PS:值噪聲看起來是一塊一塊的,為了消除這種塊狀的效果,在 1985 年 Ken Perlin 開發了另一種 noise 演算法 Gradient Noise(梯度噪聲),也就是後面的內容。
參考內容:https://thebookofshaders.com/11/?lan=ch
http://www.paulinternet.nl/?page=bicubic
https://blog.csdn.net/yolon3000/article/details/75145035

