KMP演算法的簡單理解 【筆記】
//本文除實現程式碼外全部為原創內容 轉載請註明出處 程式碼來自這裡
kmp演算法是一種改進的字串匹配演算法,由D.E.Knuth與V.R.Pratt和J.H.Morris同時發現,故稱KMP演算法
字串匹配:從字串T中尋找字串P出現的位置(P遠小於T)。其中P稱為“模式”。
KMP演算法對模式串進行O(m)的預處理後只需對文字T掃描一次即可找到匹配,所以時間複雜度為O(n+m)。
先不管O(m)的預處理,直接看O(n)的掃描。
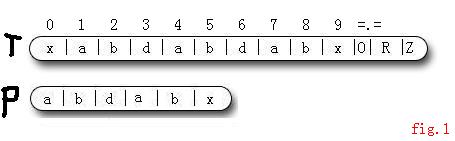
對於下圖的字串匹配:(圖1)
1 :i=0 , j=0 , 判斷T[i] != P[j],則 i++.
2 : i=1, j = 0 , T[i]==P[j] , 則i++,j++
--------------
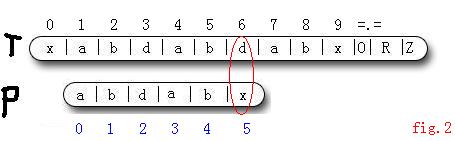
3 : 依次判斷T[2...5] == P [1...4] , 此時i = 6, j = 5 . T[i] != P[j] . (圖2)
如果使用BF演算法, i 指標在此時匹配失敗後會回溯, 然後重新進行匹配 .
KMP演算法中則不對 i 指標進行回溯, 而是修改 j 指標. 此時執行操作 j = next[j] = 2 , 繼續進行匹配; 其中next[]陣列是通過O(m)的預處理求得的, 暫時不管
--------------
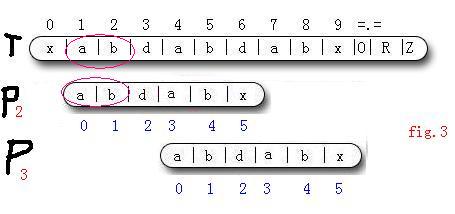
4:(圖3中, P2的 j 指標是圖2中的 j 指標)由於我們從T[1]開始匹配直到T[6]才出現匹配失敗的情況, 所以T[1...5]==P[0...4]. 很明顯圖中圈出的兩個串相等, 即 P[0 , 1] == T[1 , 2]
--------------
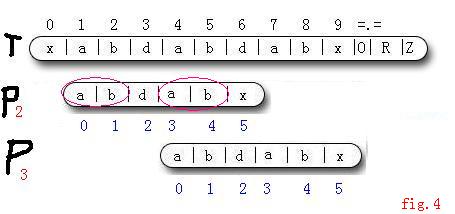
5:通過觀察我們又能發現, P[0 , 1] == P[3 , 4]; (這就是O(m)預處理出的next[]陣列中值的意義 , next[5] = 2 , 則P[0...2-1] == P[5-2...5-1])
同步驟4,由於直到T[6]才出現匹配失敗, 所以又P[3 , 4] == T[4 , 5] . 所以P[0 , 1] == T[4 , 5].
在對 j 指標進行 j = next[j] 操作後, P3 [0 , 1] 就對應著P2 [3 , 4]. 即P3[0 , 1] == T[4 , 5] . 所以KMP演算法才會直接將j 指標跳到2而不是0 , 省去了對前一部分的匹配 , 也保證了不會漏掉匹配
6:P[0...5] == T[4...9] , 匹配成功.
--------------
在對next[]的預處理中 , 如果找不到一個像上面的P[2]一樣合適的位置 , 就只能從P[0]開始匹配 , 並且在當前的 i 位置不會找到匹配了 ,所以next = -1. 程式執行j = next[j] = -1後 , 在下一次迴圈中 判斷j==-1 就執行i++,j++. 通過這樣處理, 省去了 i 指標的回溯 , 降低了時間複雜度 . 因為這樣操作每次匹配無論成功還是失敗都會有 i++ , 所以時間複雜度是O(n)
C/C++ code:
int KMPMatch(char *s,char *p)
{
int next[100];
int i,j;
i=0;
j=0;
getNext(p,next); //預處理求next[]
while(i<strlen(s))
{
if(j==-1||s[i]==p[j])
{
i++;
j++;
}
else
{
j=next[j]; //消除了指標i的回溯
}
if(j==strlen(p)) //匹配成功
return i-strlen(p);
}
return -1;
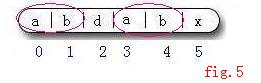
}接下來再看O(m)的預處理。回顧一下剛剛的模式字串P(圖5)
我們剛剛用到了j = next[j] = next[5] = 2, 當時j =5 , j-1 =4 .
觀察位置2的性質. 在子串P[0...j-1]即 P[01234] 中 , P[0]P[1] == P[3]P[4] 即 P[0...2-1] == P[5-2...5-1]
也就是說, 串P[0]P[1]即串P[3]P[4]既是字串P[0...4]的真字首, 又是它的真字尾. 重新看圖4就能明白 , 只要滿足這個性質, 就能保證語句 j = next[j] 的正確性.
結論 若next[j]=k , 則k為滿足 P[0...k-1] == P[j-k ... j-1] 且 k<j 的最大值. 如果找不到這樣的k , next[j]=-1.
顯然next[0]=-1 , next[1] = 0
預處理的方法(這裡只介紹遞推方法)
如果有next[j]=k, 則有P[0...k-1] == P[j-k ... j-1]
1) 如果P[j] == P[k]
P[0...k-1] + P[k] == P[j-k ... j-1] + P[j] 即 P[0...k] == P [j-k ... j]
所以next[j+1] = k + 1 = next[j] + 1
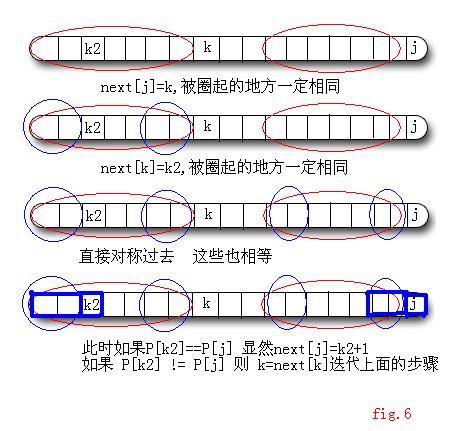
2) 如果P[j] != P[k], 那麼可以看做模式匹配的問題,匹配失敗的時候, 顯然k=next[k].
具體:(圖6)設next[j]=k, next[next[j]] = next[k] = k2
C/C++ code:
void getNext(char *p,int *next)
{
int j,k;
next[0]=-1;
j=0;
k=-1;
while(j<strlen(p)-1)
{
if(k==-1||p[j]==p[k]) //匹配的情況下,p[j]==p[k]
{
j++;
k++;
next[j]=k;
}
else //p[j]!=p[k]
k=next[k];
}
}