深度強化學習cs294 Lecture6: Actor-Critic Algorithms

• 1. Improving the policy gradient with a critic
• 2. The policy evaluation problem
• 3. Discount factors
• 4. The actor-critic algorithm
• State-dependent baselines

複習一下上節課的策略梯度演算法。主要就是對目標函式的定義以及梯度的計算。還有一些減小方差的方法以及Importance Sampling的方法。

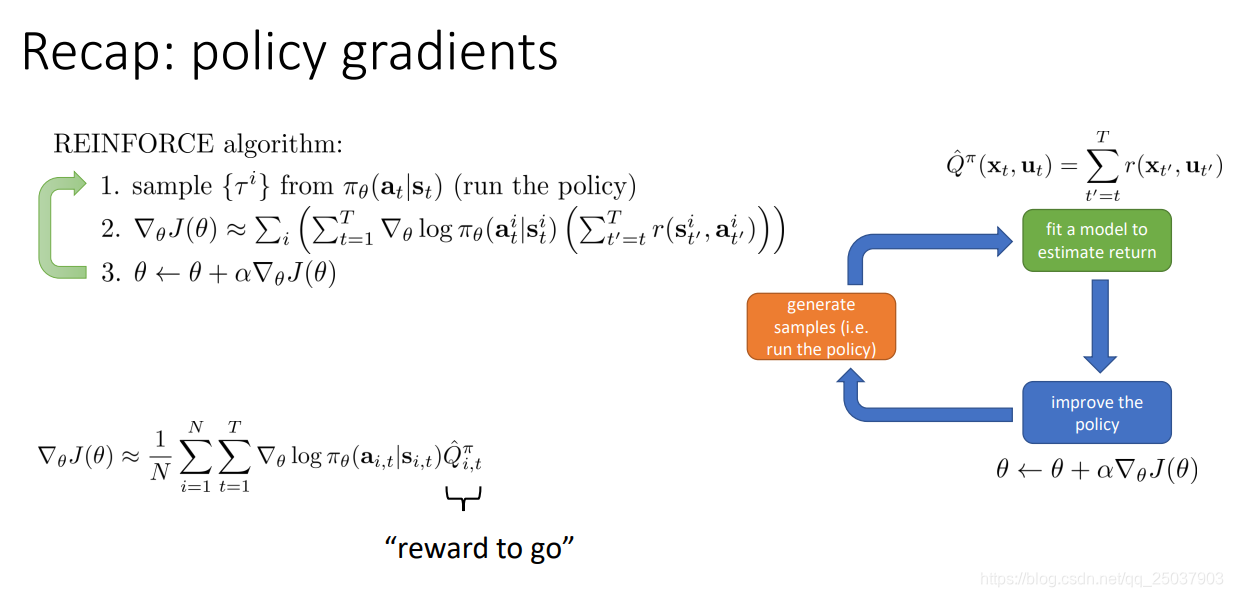
1. Improving the policy gradient with a critic

在公式裡從當前開始得到的反饋值之和 ${\hat{Q}}_{i,t}^{}$

π \widehat{Q}^{\pi}_{i,t} 有一個更好的估計方式：

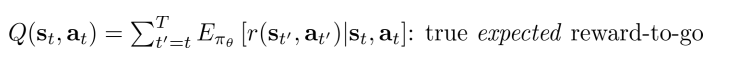
這表示當前狀態 $s_{t}$

採取了動作 $a_{t}$之後後面會得到的所有反饋和的期望值。對應的有一個在當前狀態 $s_{t}$的期望值，就是對Q進行在 $a_{t}$上求期望：

在policy gradient方法中使用一個常數b作為一個baseline來減小梯度的方差。這裡的b就是對Q值的一個平均，那麼就可以使用V來替代，而原本的 $\widehat{Q}^{\pi}_{i,t}$也可以用新的期望值 $Q^{\pi}(s_{t},a_{t})$替代。這樣就得到了兩個期望值的差值，我們把這個值叫做advantage函式。

使用了advantage函式的梯度求導，如果advantage函式估計得越準確，那麼梯度的方差就會越小。而原來的使用一個序列的反饋值之和減去b的方式，方差更大。不過是一個無偏估計。

因此使用新的期望函式來計算梯度，但是需要計算三個不同的值 $Q, V,A$比較麻煩，可以看一下它們之間的關係。因為 $Q^{\pi}(s_{t},a_{t})$對應的是一個固定的狀態動作對 $(s_{t},a_{t})$，因此有一步的反饋值r已經固定不變了，也就是 $Q^{\pi}(s_{t},a_{t}) = r(s_{t},a_{t})+E_{s_{t+1}\sim p(s_{t+1}|s_{t})}[V^{\pi}(s_{t+1})]$，如果採用取樣近似期望的形式可以寫為 $Q^{\pi}(s_{t},a_{t}) \approx r(s_{t},a_{t})+V^{\pi}(s_{t+1})$。這樣我們在計算梯度的過程中只需要計算一個期望函式 $V^{\pi}(s_{t})$即可，這個一般也使用神經網路來進行逼近。

2. The policy evaluation problem

從期望值V的定義可以看出，強化學習的目標函式其實就是這個值關於初始狀態 $s_{1}$的期望值。也就是說計算 $V^{\pi}$就是對當前的策略進行一個評價，評價當前策略是好是壞。我們有兩種MC方法能夠估算出對應的V值，但是第二種對序列進行平均的方式不太好實現，因此一般使用第一個簡單的形式：

因此我們就有了目標label，下面用監督學習的方式來對這個V值做一個擬合即可，擬合的目標函式是均方誤差，這樣訓練就能得到一個能夠擬合出狀態值函式的神經網路：

不過實際上我們可以做得更精確一些。因為這裡直接使用了一個序列樣本的反饋和作為目標值，實際上方差會很大。可以利用一個近似的方式來減小方差。 $y_{i,t} = \sum_{t'=t}^{T}E_{\pi_{\theta}}[r(s_{t'},a_{t'})|s_{i,t}]\approx r(s_{i,t},a_{i,t})+V^{\pi}(s_{t})\approx r(s_{i},a_{i})+\widehat{V}^{\pi}_{\phi}(s_{i,t+1})$。這個方法叫做自舉。其中使用了下一個狀態的估計值來計算前一個時間狀態的估計值。這樣做能夠減小方差，因為計算的結果不是一個取樣而是一個期望。但是會引入一些誤差，因為當前的估計函式並不是真實的V值。

有很多成功的例子都使用了這個方法，比如TD-gammon和Alphago。

於是我們就得到了一個新的形式的actor-critic演算法：

3. Discount factors

上面的actor-critic演算法裡第一步還需要取樣一整個序列。想要變成每次只採樣一個狀態即可，還需要先引入Discount factors的設定。

因為值函式V的定義是當前狀態以後所有反饋值的和，在有限步長的任務中沒有問題，但是如果是一個