深度強化學習cs294 Lecture5: Policy Gradients Introduction
深度強化學習cs294 Lecture5: Policy Gradients Introduction
首先回顧強化學習的目標。強化學習問題可以看成一個建立在馬爾科夫決策過程之上的序列決策問題,其中要調整的部分是採取動作的策略函式,現在很多都使用神經網路來得到。強化學習的目標就是找到一個策略,能夠最大化一個序列反饋和的期望值。

而對於序列反饋期望值的計算可以分為兩種情況,一種是有限步數的情況,一種是無限步數的情況。這兩種情況實際上是一樣的,不過寫為期望的形式略有不同。無限步長的情況也可以根據一個最終的穩定分佈寫為類似的形式。今天我們只關注有限步長的形式,在後面講到actor-critic演算法時會講到有限步延伸到無限步。實際上有限步長裡最優的策略是個時變函式,當然我們這裡不考慮時變這一點,依然當做是一個與時間無關的函式。

因為序列的概率分佈實際上無法得到,因此我們一般都是用取樣的方式來近似得到期望的結果。
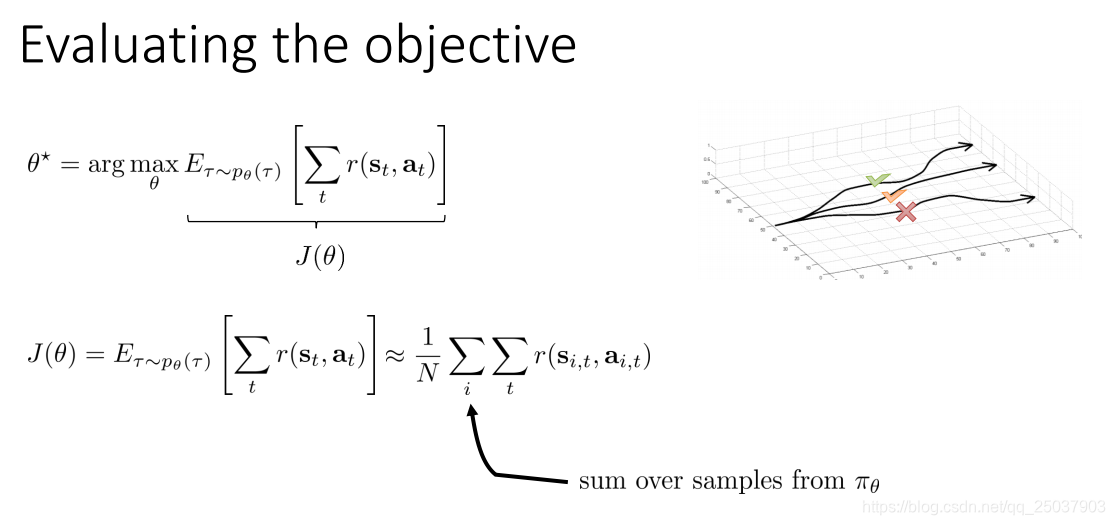
1. The policy gradient algorithm
我們知道了強化學習的目標是求得最大化期望反饋和的策略引數,因此有一種比較直接的方式就是對目標函式進行直接梯度上升法求解。
如圖所示,其中對策略求導的部分用對數求導的等式可以讓梯度也寫為一個期望的形式:

因為公式裡一直用的是序列
的概率,而序列
的概率實際上是一堆乘積的形式。寫開之後求log變為和的形式,再求導去掉部分無關項:
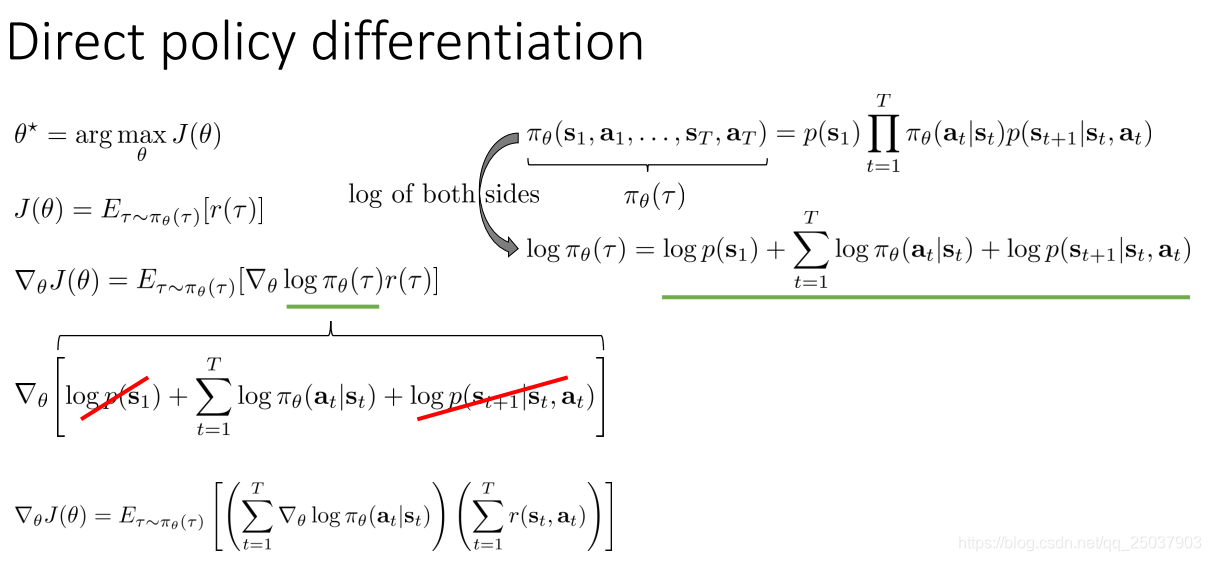
期望值括號裡的部分已經可以得到,但是期望依然無法求解。不過還是很簡單地使用取樣逼近期望值即可,於是直接進行policy gradient的演算法就得到了,這個演算法也叫作REINFORCE演算法:
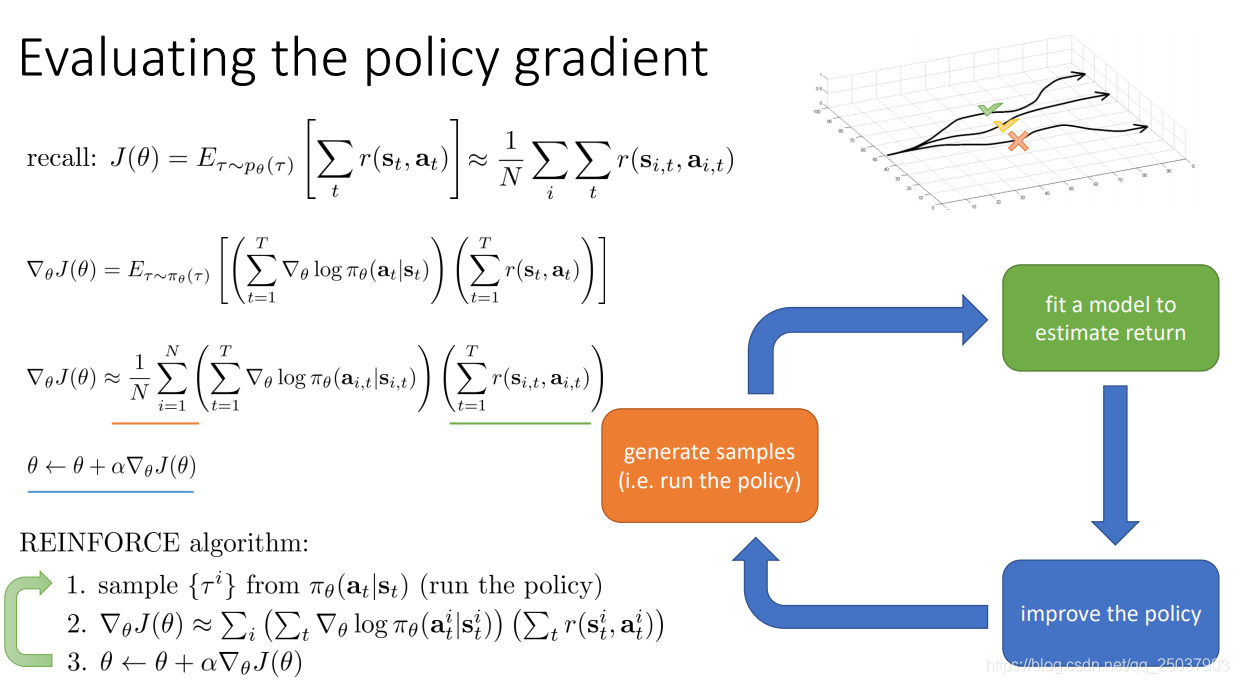
2. What does the policy gradient do?
來進一步的觀察這個策略梯度的演算法。用之前模仿學習裡面講到的例子,我們發現與直接進行最大似然的方法相比,策略梯度法的梯度僅僅是相當於對每一項使用了對應序列反饋值和來進行加權:
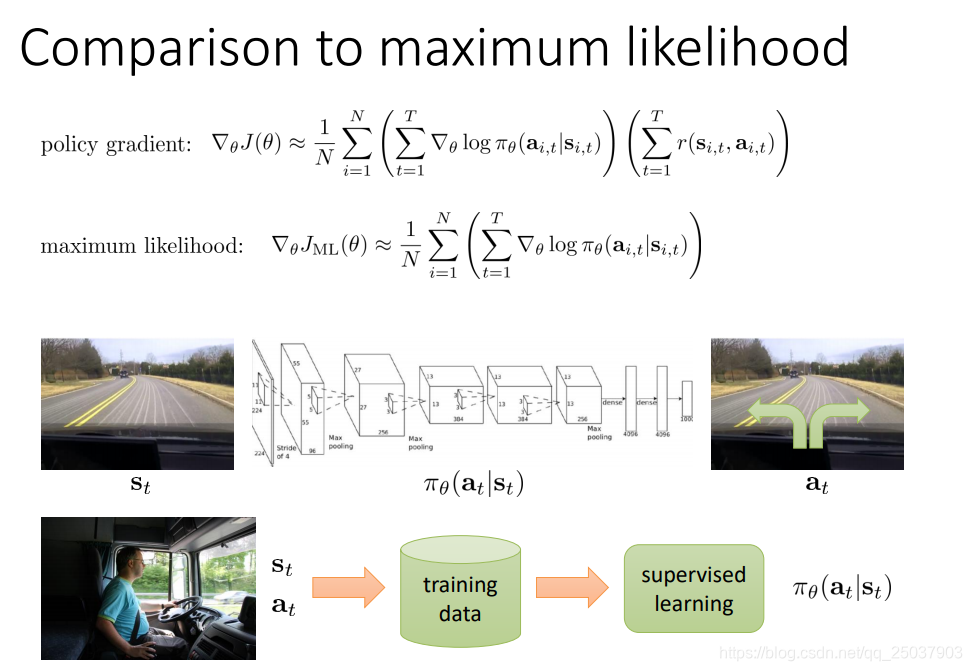
這個演算法相當於對於表現的比較好也就是反饋和比較大的例子,選擇增大其出現的可能性,而表現得比較差的就減小其可能性。與最大似然的方法相比區別在於對每個樣本是區別對待的。這個概念也就是trial and error的想法。

而對於部分可觀察的POMDP來說,這個演算法也可以直接應用。因為這個演算法在推導的過程中,並沒有使用MDP裡狀態動作對的馬爾科夫性質。

但是這個演算法有個缺點,那就是它的演算法計算梯度的時候,方差特別大。可以用一個示意圖來簡單描述。
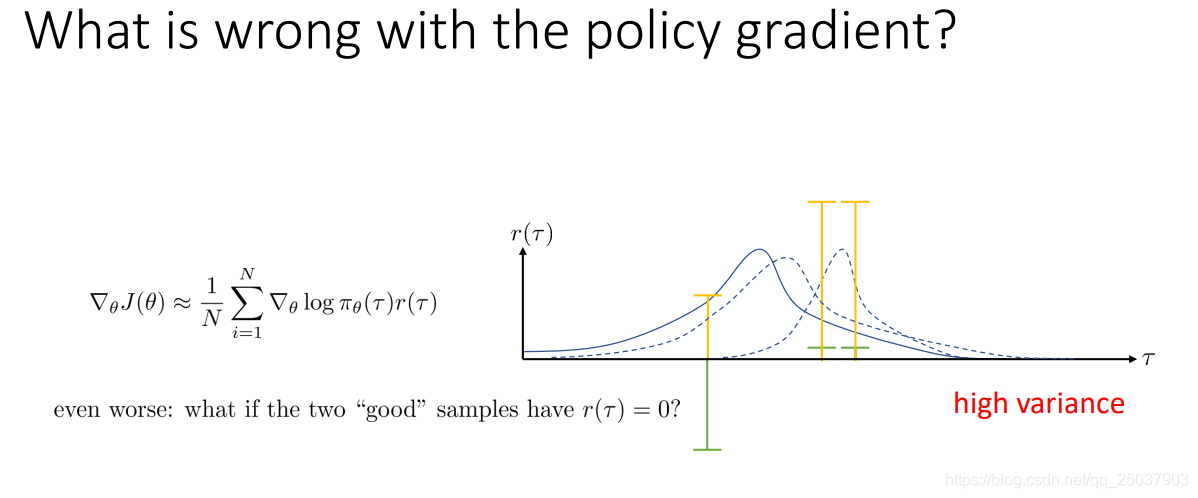
假設序列分佈作為橫軸,反饋值之和作為縱軸。如果有三個取樣點如綠色橫線表示,有兩個表現為正,一個為負,那麼下一次的梯度更新後的分佈就會網右邊兩個靠近,遠離左邊的例子。但是如果對每個序列的反饋和同時加一個常數,就會變成黃色的表示,那麼這三個點更新後的概率分佈都會變大。對於極端的例子比如把右邊兩個例子的反饋減為0,那麼更新後的分佈就不會關注這兩個例子。顯然這是不對的,因為實際上的策略不應該被反饋的絕對值影響,而只關注它們的相對值。
在解決這個問題之前先回顧一下剛剛講過的內容:
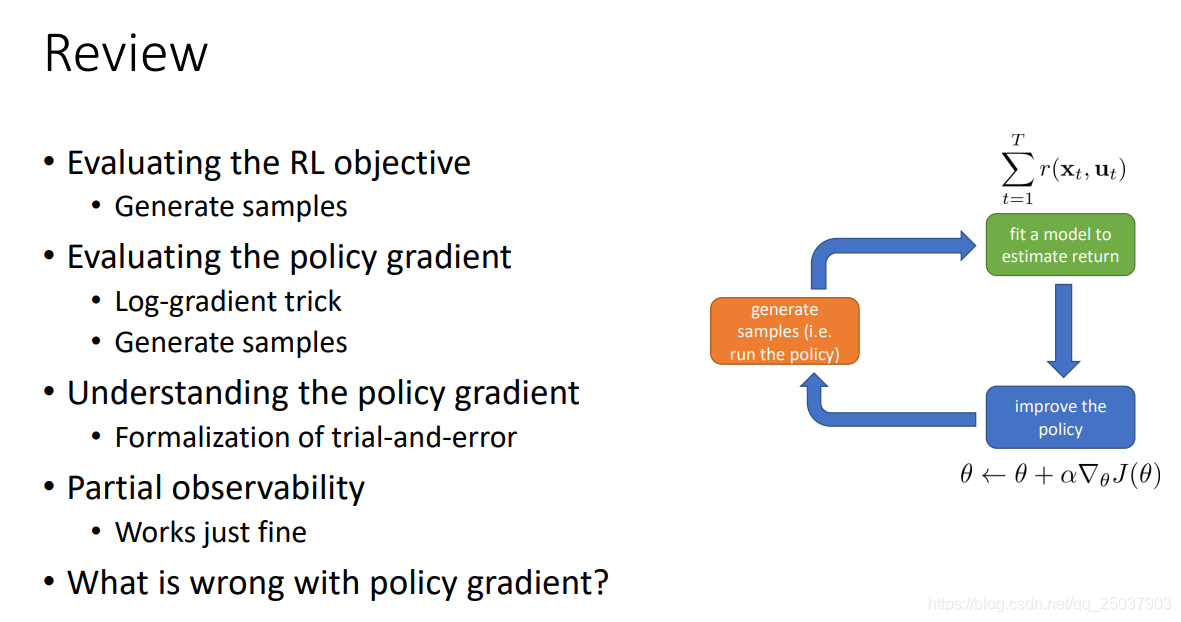
3. Basic variance reduction: causality
直接使用策略梯度演算法REINFORCE會導致更新梯度的時候方差太大,因此需要考慮減小方差的方法。首先想到的一個方法就是利用因果律。
因果律講的是,時間t+1時發生的事情不會影響到t和t之前發生的。這個規律應用在目標函式梯度的計算時候也可以用上。那就是對於時間t時候對應的策略,與t之前得到的反饋值是無關的。因此在計算反饋值的時候不需要從
開始計算,而是從
開始計算。這個值剛好是後面要講的
值。

使用這種簡單的方式最終減小了目標函式梯度的大小,因此就減小了對應的方差。
4. Basic variance reduction: baseline
還有一種減小方差的方式是,在計算每個序列反饋和的時候減掉序列和的期望值。當然期望值使用的是取樣平均替代。這樣做相當於是增大了表現得比平均更好的序列的概率,而抑制了表現得比平均更差的序列發生的概率。

當然這裡存在一個問題,就是在計算梯度的時候隨意加入一個值是否合理。回憶一下目標函式梯度的計算,加了個常數b相當於是加了如下一項:
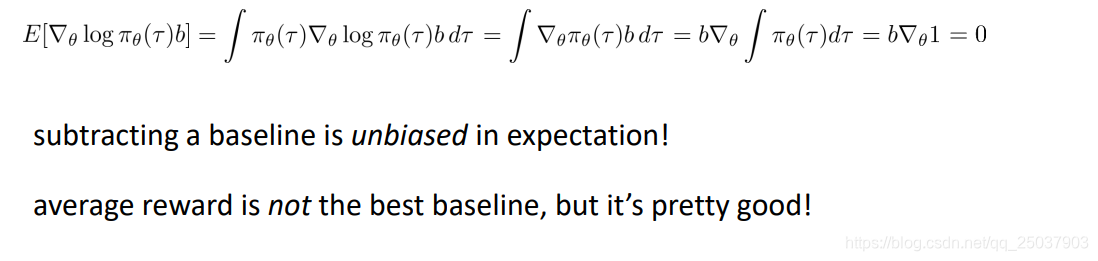
可以看出推導的結果是0,也就是說取樣計算加入常數b之後的估計依然是原來的無偏估計,沒有問題。
不過加入這個序列期望和的平均值並不是一個最優的方式,當然表現得已經是足夠好了。現在來計算一下最優的解是啥:

可以看到最後的結果相當於是序列對應的概率的log求梯度之後的平方加權的反饋和的加權期望。計算起來稍微複雜了一些,帶來的增益沒那麼大,因此我們一般還是會選擇直接使用期望和的平均值。
總結一下減少方差的方法:
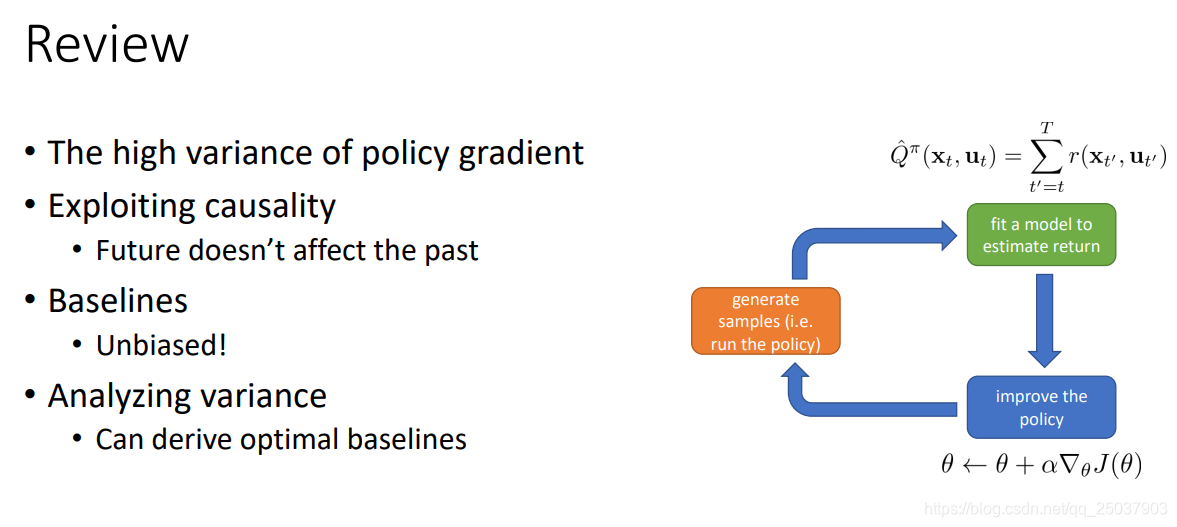
5. Off-policy learning & importance sampling
策略梯度法是一個on-policy的方法。這意味著每一次策略的更新都需要拋棄之前所有的取樣。因此非常耗時費力:

有一種方式能夠讓更新後的策略計算目標函式時候依然能夠使用以往的取樣序列,這個方法就叫做importance sampling演算法。其實像很簡單,如圖綠框所示,起始就是加一項概率比的係數,使最終結果變為另一個分佈的期望:

用在強化學習裡,我們發現序列
在當前策略下發生的概率無法計算。但是還好我們只需要兩個序列概率的比值,因此可以消掉無法知道的轉移概率與初始概率。
這樣我們也能夠寫出使用了importance sampling方法的目標函式的梯度:

於是我們發現,之前使用的on-policy形式的方法只不過是這裡的一個
的特例,相等時只要把其中的概率比寫為1即可。
但是我們又得到了一個新的問題,那就是importance sampling加入的概率比是個連乘項,很容易變得太大或太小。因此還需要進一步的處理。

可以把對應的概率比連乘的項寫為兩個部分。前一個部分的概率表示的是從初始狀態開始轉移到當前狀態的概率之比。這發生在時間t之前,因此不會受到修改引數的影響。後面一部分的概率連乘可以直接忽略,這節課後面的部分會講這樣做會得到policy iteration的結果。
忽略了後面的部分之後結果太大或太小的情況就緩解了很多,但是那裡依然有一個指數項。於是繼續考慮寫為另外的形式。因為需要對狀態動作對的聯合概率求期望,可以寫為先對狀態求期望,然後對動作求。但是我們並不知道
,因此直接忽略掉這一項的結果。後面會解釋這樣做的合理性。

6. Policy gradient in practice
下面講一點實際的應用。如何在深度學習包裡計算這個對應的目標函式的梯度。直接進行每一個序列每個時間點進行梯度計算然後相加是不行的。無法並行加速。

可以來觀察一下最大似然情況下是如何進行計算的。

因此我們可以類似地構造一個假的loss函式來讓程式進行梯度計算,加入我們把loss設計為如下形式:

那麼這樣進行梯度計算之後的結果正是我們想要的目標函式的梯度。

還有一些在實際使用策略梯度法時候的建議:1.記住梯度的方差非常大。2.可以考慮用比較大的batch。 3.用tweaking learning比較難。

回顧一下:
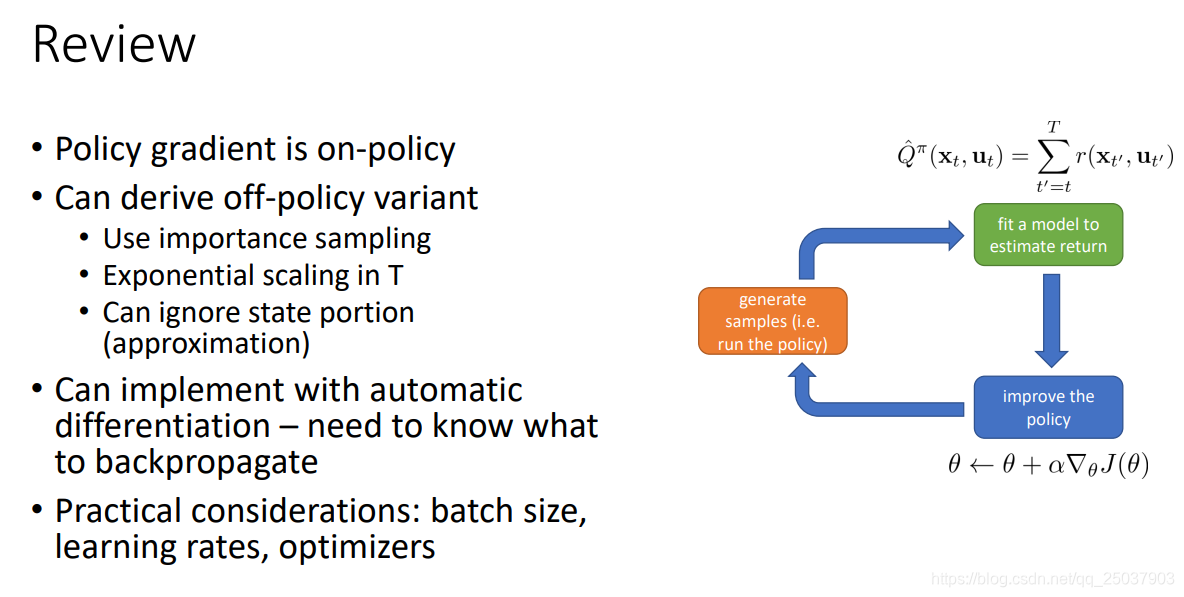
7. Policy gradient examples
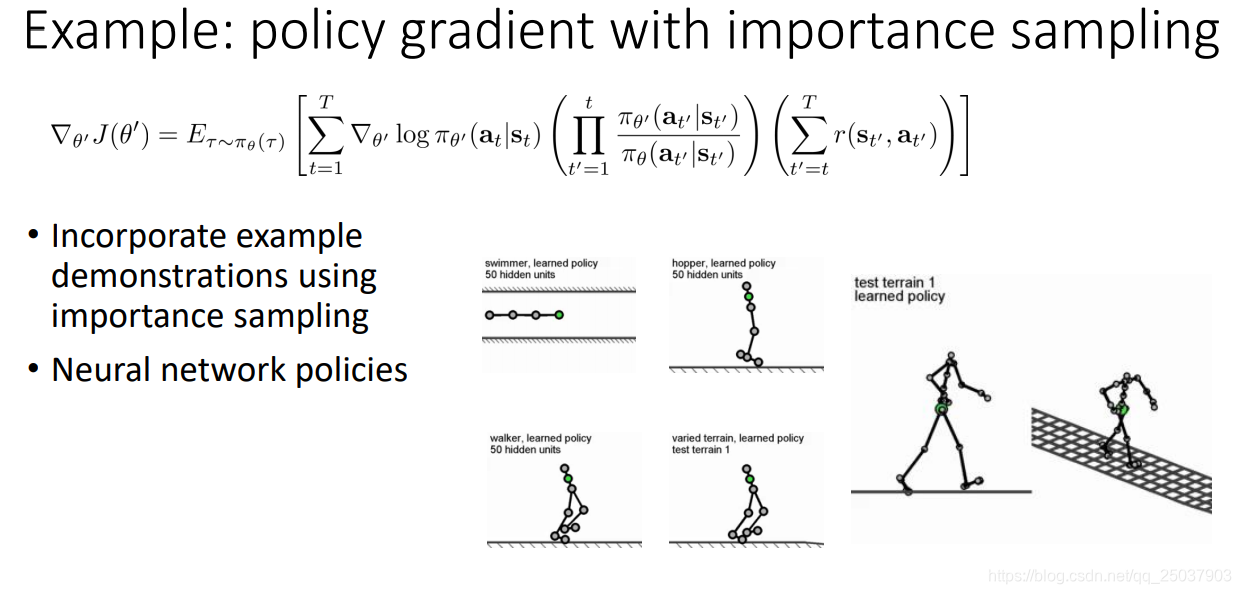
後面提到了幾個使用策略梯度的例子,似乎TRPO後面會詳細講。

最後是一些推薦的文章:

路漫漫其修遠兮,吾將早晚聽不懂。
