人工智慧中的很多應用問題需要演算法在每個時刻做出決策並執行動作。對於圍棋，每一步需要決定在棋盤的哪個位置放置棋子，以最大可能的戰勝對手；對於自動駕駛演算法，需要根據路況來確定當前的行駛策略以保證安全的行駛到目的地；對於機械手，要驅動手臂運動以抓取到設定的目標物體。這類問題有一個共同的特點：要根據當前的條件作出決策和動作，以達到某一預期目標。解決這類問題的機器學習演算法稱為強化學習（reinforcement learning，RL）。雖然傳統的強化學習理論在過去幾十年中得到了不斷的完善，但還是難以解決現實世界中的複雜問題。

深度強化學習（DRL，deep reinforcement learning）是深度學習與強化學習相結合的產物，它集成了深度學習在視覺等感知問題上強大的理解能力，以及強化學習的決策能力，實現了端到端學習。深度強化學習的出現使得強化學習技術真正走向實用，得以解決現實場景中的複雜問題。從2013年DQN（深度Q網路，deep Q network）出現到目前為止，深度強化學習領域出現了大量的演算法，以及解決實際應用問題的論文。在這篇文章中，SIGAI將對深度強化學習的演算法與應用進行總結。整個綜述分為上下兩篇，本篇介紹強化學習的基本原理，深度強化學習的基本思想，以及基於價值函式的深度強化學習演算法。下篇介紹基於策略的深度強化學習演算法，基於搜尋與監督的深度強化學習演算法，以及深度強化學習演算法的應用情況與未來的方向。

什麼是強化學習

強化學習[1]是一類特殊的機器學習演算法，借鑑於行為主義心理學。與有監督學習和無監督學習的目標不同，演算法要解決的問題是智慧體（agent，即執行強化學習演算法的實體）在環境中怎樣執行動作以獲得最大的累計獎勵。例如，對於自動行駛的汽車，強化學習演算法控制汽車的動作，保證安全行駛到目的地。對於圍棋演算法，演算法要根據當前的棋局來決定如何走子，以贏得這局棋。對於第一個問題，環境是車輛當前行駛狀態（如速度）、路況這樣的引數構成的系統的抽象，獎勵是我們期望得到的結果，即汽車正確的在路面上行駛，到達目的地而不發生事故。

很多控制、決策問題都可以抽象成這種模型。和有監督學習類似，強化學習也有訓練過程，需要不斷的執行動作，觀察執行動作後的效果，積累經驗形成一個模型。與有監督學習不同的是，這裡每個動作一般沒有直接標定的標籤值作為監督訊號，系統只給演算法執行的動作一個反饋，這種反饋一般具有延遲性，當前的動作所產生的後果在未來才會完全體現，另外未來還具有隨機性，例如下一個時刻路面上有哪些行人、車輛在運動，演算法下一個棋子之後對手會怎麼下，都是隨機的而不是確定的。當前下的棋產生的效果，在一局棋結束時才能體現出來。

強化學習應用廣泛，被認為是通向強人工智慧/通用人工智慧的核心技術之一。所有需要做決策和控制的地方，都有它的身影。典型的包括遊戲與博弈，如打星際爭霸、Atari遊戲：

演算法需要根據當前的遊戲畫面和狀態決定其要執行的動作，如按遊戲的鍵盤、手柄，滑鼠。

 

圍棋，象棋等棋類遊戲：

演算法需要根據當前的棋局決定當前該怎麼走子。

 

自動駕駛系統/無人車：

演算法需要根據當前的路況，無人車自身的狀態（如速度、加速度）決定其行駛的行為，如控制方向盤，油門，剎車等。

 

機器人控制：

機器人要根據當前所處的環境，自身的狀態，決定其要執行的動作。

所有這些問題總計起來都有一個特點，即智慧體需要觀察環境和自身的狀態，然後決定要執行的動作，以達到想要的目標：

智慧體是強化學習的動作實體。對於自動駕駛的汽車，環境是當前的路況；對於圍棋，狀態是當前的棋局。在每個時刻，智慧體和環境有自己的狀態，如汽車當前位置和速度，路面上的車輛和行人情況。智慧體根據當前狀態確定一個動作，並執行該動作。之後它和環境進入下一個狀態，同時系統給它一個反饋值，對動作進行獎勵或懲罰，以迫使智慧體執行期望的動作。

強化學習是解決這種決策問題的一類方法。演算法要通過樣本學習得到一個對映函式，稱為策略函式，其輸入是當前時刻環境資訊，輸出是要執行的動作：

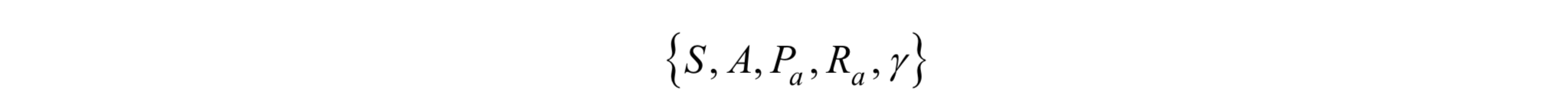
其中s為狀態，a為要執行的動作，狀態和動作分別來自狀態集合和動作集合。動作和狀態可以是離散的，如左轉30度、右轉30度，也可以是連續的實數，如左轉30度、右轉30度。對於前者，動作和狀態集合是有限集，對於後者，是無限集。執行動作的目標是要達到某種目的，如無人汽車安全的行駛，贏得本次圍棋比賽，用回報函式對此進行建模。

馬爾可夫決策過程

強化學習要解決的問題可以抽象成馬爾可夫決策過程（Markov Decision Process，簡稱MDP）。馬爾可夫過程的特點是系統下一個時刻的狀態由當前時刻的狀態決定，與更早的時刻無關。與馬爾可夫過程不同的是，在MDP中系智慧體可以執行動作，從而改變自己和環境的狀態，並且得到懲罰或獎勵。馬爾可夫決策過程可以表示成一個五元組：

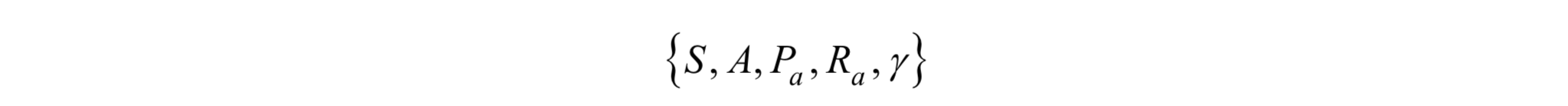
其中S和A分別為狀態和動作的集合。假設t時刻狀態為st，智慧體執行動作a，下一時刻進入狀態st+1。這種狀態轉移與馬爾可夫模型類，不同的是下一時刻的狀態由當前狀態以及當前採取的動作決定，是一個隨機性變數，這一狀態轉移的概率為：

 

這是當前狀態為s時行動作a，下一時刻進入狀態s'的條件概率。下一時刻的狀態與更早時刻的狀態和動作無關，狀態轉換具有馬爾可夫性。有一種特殊的狀態稱為終止狀態（也稱為吸收狀態），到達該狀態之後不會再進入其他後續狀態。對於圍棋，終止狀態是一局的結束。

執行動作之後，智慧體會收到一個立即回報：

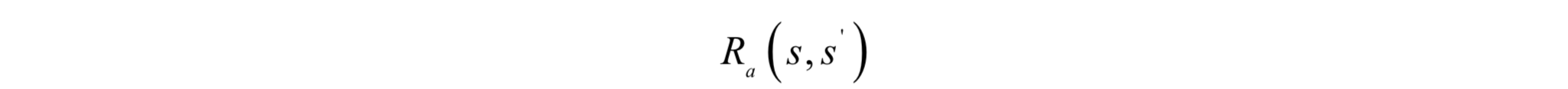
立即回報與當前狀態、當前採取的動作以及下一時刻的狀態有關。在每個時刻t，智慧體選擇一個動作at執行，之後進入下一狀態st+1，環境給出回報值。智慧體從某一初始狀態開始，每個時刻選擇一個動作執行，然後進入下一個狀態，得到一個回報，如此反覆：

問題的核心是執行動作的策略，它可以抽象成一個函式π，定義了在每種狀態時要選擇執行的動作。這個函式定義了在狀態s所選擇的動作為：

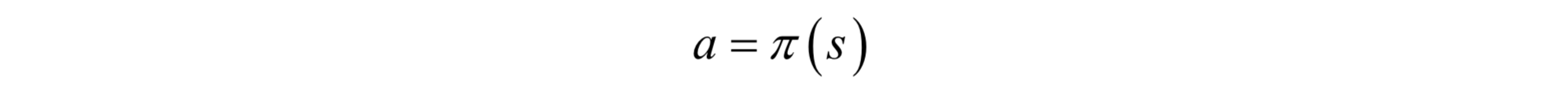
這是確定性策略。對於確定性策略，在每種狀態下智慧體要執行的動作是唯一的。另外還有隨機性策略，智慧體在一種狀態下可以執行的動作有多種，策略函式給出的是執行每種動作的概率：

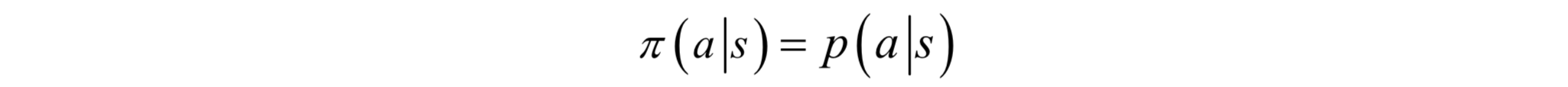
即按概率從各種動作中隨機選擇一種執行。策略只與當前所處的狀態有關，與時間點無關，在不同時刻對於同一個狀態所執行的策略是相同的。

強化學習的目標是要達到某種預期，當前執行動作的結果會影響系統後續的狀態，因此需要確定動作在未來是否能夠得到好的回報，這種回報具有延遲性。對於圍棋，當前走的一步棋一般不會馬上結束，但會影響後續的棋局，需要使得未來贏的概率最大化，而未來又具有隨機性，這為確定一個正確的決策帶來了困難。

選擇策略的目標是按照這個策略執行後，在各個時刻的累計回報值最大化，即未來的預期回報最大。按照某一策略執行的累計回報定義為：

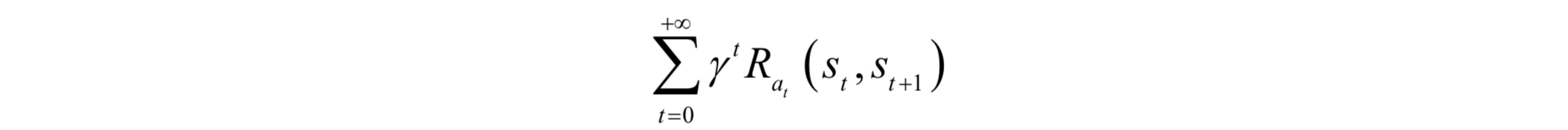
這裡使用了帶衰減係數的回報和。按照策略π，智慧體在每個時刻t執行的動作為：

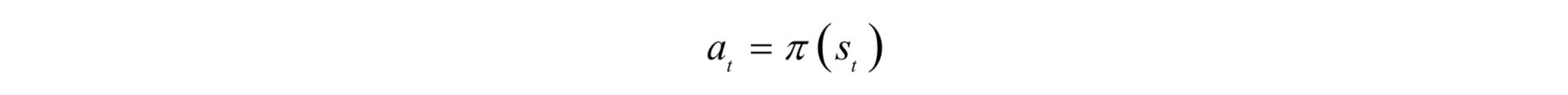
其中γ稱為折扣因子，是[0, 1]之間的一個數。在每個時刻t執行完動作at得到的回報為：

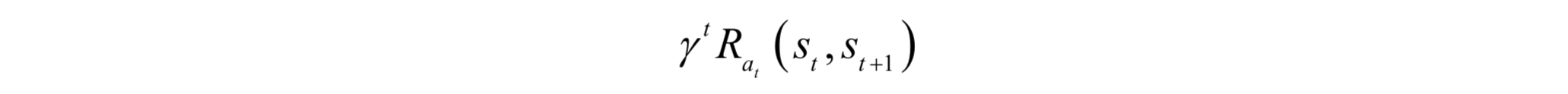
使用折扣因子是因為未來具有更大的不確定性，所以回報值要隨著時間衰減。另外如果不加上這種按照時間的指數級衰減會導致整個求和項趨向於無窮大。這裡假設狀態轉移概率以及每個時刻的回報是已知的，演算法要尋找最佳策略來最大化上面的累計回報。

如果每次執行一個動作進入的下一個狀態是確定的，則可以直接用上面的累計回報計算公式。如果執行完動作後進入的下一個狀態是隨機的，則需要計算各種情況的數學期望。類似於有監督學習中需要定義損失函式來評價預測函式的優劣，在強化學習中也需要對策略函式的優劣進行評價。為此定義狀態價值函式的概念，它是在某個狀態s下，按照策略π執行動作，累計回報的數學期望，衡量的是按照某一策略執行之後的累計回報。狀態價值函式的計算公式為：

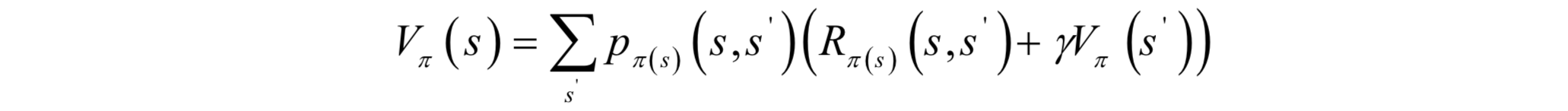
這是一個遞迴的定義，函式的自變數是狀態與策略函式，將它們對映成一個實數，每個狀態的價值函式依賴於從該狀態執行動作後能到達的後續狀態的價值函式。在狀態s時執行動作π(s)，下一時刻的狀態s'是不確定的，進入每個狀態的概率為pπ(s)(s,s'),當前獲得的回報是Rπ(s)(s,s')，因此需要對下一時刻所有狀態計算數學期望即概率意義上的均值，而總的回報包括當前的回報，以及後續時刻的回報值之和即Vπ(s')。在這裡R(s)表示當前時刻獲得的回報。如果是非確定性策略，還要考慮所有的動作，這種情況的狀態價值函式計算公式為：

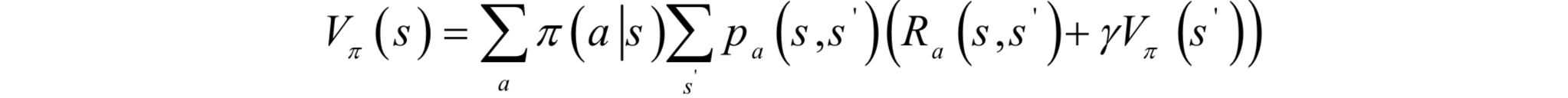
對於終止狀態，無論使用什麼策略函式，其狀態價值函式為0。類似的可以定義動作價值函式。它是智慧體按照策略π執行，在狀態s時執行具體的動作a後的預期回報，計算公式為：

動作價值函式除了指定初始狀態s與策略π之外，還指定了在當前的狀態s時執行的動作a。這個函式衡量的是按照某一策略，在某一狀態時執行各種動作的價值。這個值等於在當前狀態s下執行一個動作後的立即回報Ra(s,s')，以及在下一個狀態s'時按照策略π執行所得到的狀態價值函式Vπ(s')之和，此時也要對狀態轉移pa(s,s')概率求數學期望。狀態價值函式和動作值函式的計算公式稱為貝爾曼方程，它們是馬爾可夫決策過程的核心。

 

因為演算法要尋找最優策略，因此需要定義最優策略的概念。因為狀態價值函式定義了策略的優劣，因此我們可以根據此函式值對策略的優劣進行排序。對於兩個不同的策略π和π'，如果對於任意狀態s都有：

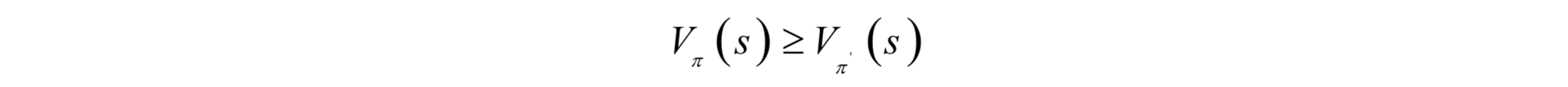
則稱策略π優於策略π'。對於任意有限狀態和動作的馬爾可夫決策過程，都至少存在一個最優策略，它優於其他任何不同的策略。

一個重要結論是，所有的最優策略有相同的狀態價值函式和動作價值函式值。最優動作價值函式定義為：

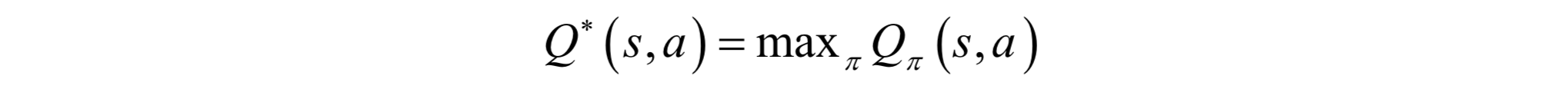
對於狀態-動作對(s,a)，最優動作價值函式給出了在狀態s時執行動作a，後續狀態時按照最優策略執行時的預期回報。找到了最優動作價值函式，根據它可以得到最優策略，具體做法是在每個狀態時執行動作價值函式值最大的那個動作：

因此可以通過尋找最優動作價值函式而得到最優策略函式。如果只使用狀態價值函式，雖然能找到其極值，但不併知道此時所採用的策略函式。

最優狀態價值函式和最優動作價值函式都滿足貝爾曼最優性方程。對於狀態價值函式，有：

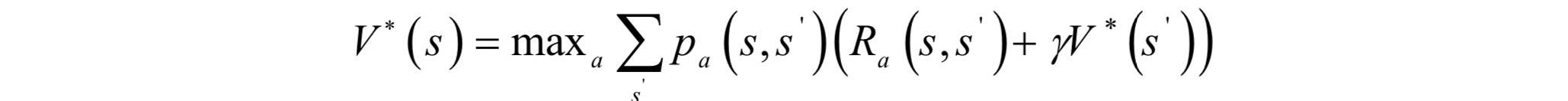
上式的意義是對任何一個狀態s，要保證一個策略π能讓狀態價值函式取得最大值，則需要本次執行的動作a所帶來的回報與下一狀態s'的最優狀態價值函式值之和是最優的。對於動作價值函式，類似的有：

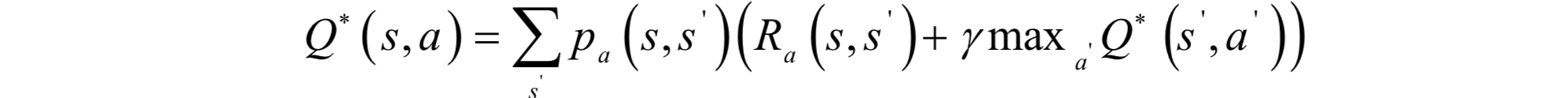
其意義是要保證一個策略使得動作價值函式是最優的，則需要保證在執行完本動a之後，在下一個狀態s'所執行的動作a'是最優的。對於任意有限狀態和動作的馬爾可夫決策過程，貝爾曼最優方程有唯一解，且與具體的策略無關。可以將貝爾曼最優性方程看成一個方程組，每個狀態有一個方程，未知數的數量也等於狀態的數量。

時序差分演算法

如果能知道所有狀態的狀態轉移概率，以及回報值，則理論上可以用動態規劃演算法求解，這是一種迭代法，從一個隨機設定的初始值開始，用某種規則進行迭代，直到收斂到狀態價值函式或者動作價值函式的極大值。迭代的規則一般是貝爾曼方程或貝爾曼最優性方程。

但在很多實際應用中，我們無法得到所有狀態的轉移概率，例如自動駕駛、圍棋，此時無法使用動態規劃演算法求解，只能採用隨機演算法，其核心思想是：從一個初始的隨機策略開始隨機的執行一些動作，然後觀察回報和狀態轉移，以此估計價值函式的值，或者更新價值函式的值。形象的說，就是加大效果的動作的執行力度，減小效果不好的動作的執行力度。蒙特卡洛演算法和時序差分演算法是典型的代表，在這裡我們重點介紹時序差分演算法的一種實現-Q學習。

時序差分演算法（Temporal Difference learning，簡稱TD學習）[2]在執行一個動作之後進行動作價值函式更新。TD演算法無需依賴狀態轉移概率，直接通過生成隨機的樣本來計算。TD演算法用貝爾曼方程估計價值函式的值，然後構造更新項。其典型實現有SARSA演算法和Q學習演算法。

Q學習演算法[3]是時序差分演算法的一種，它估計每個動作價值函式的最大值，通過迭代可以直接找到Q函式的極值，從而確定最優策略。Q學習訓練演算法的流程如下：

初始化，將所有非終止狀態的Q(s, a)初始化為任意值，終止狀態的初始化為0

實現時需要根據當前的動作價值函式的估計值為每個狀態選擇一個動作來執行，有3種方案。第1種是隨機選擇一個動作，稱為探索（exploration）。第2種是根據當前的動作函式值選擇一個價值最大的動作執行：

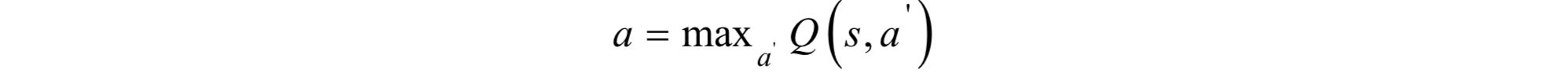
稱為利用（exploitation）。第3種是前兩者的結合，即ε-貪心策略。執行完動作之後，進入狀態s'，然後尋找狀態s'下所有動作的價值函式的極大值，構造更新項。演算法最終會收斂到動作價值函式的最優值。

用於預測時，在每個狀態下選擇函式值最大的動作執行，這就是最優策略，具體實現時同樣可以採用ε-貪心策略。

具體實現時，將所有狀態、動作的Q(s, a)儲存在一個二維表格中，先初始化，然後通過此表格來確定一些動作執行，然後更新表格的值，直到收斂。

深度強化學習的早期探索

前面介紹的Q學習都只能用於狀態和動作的集合是有限的離散基且狀態和動作數量較少的情況，狀態和動作需要人工預先設計，Q函式值需要儲存在一個二維表格中。實際應用中的場景可能會很複雜，很難定義出離散的狀態；即使能夠定義，數量也非常大，無法用陣列儲存。

對於強化學習來說，很多實際應用問題的輸入資料是高維的，如影象，聲音，演算法要根據它們來選擇一個動作執行以達到某一預期的目標。比如，對於自動駕駛演算法，要根據當前的畫面決定汽車的行駛方向和速度。經典的強化學習演算法如Q學習需要列舉出所有可能的情況（稱為狀態，這是對當前所處環境的抽象），然後進行迭代。Q學習的經典實現是列舉出所有的狀態和動作，構建Q函式表，這是一個二維的表，然後迭代計算各種狀態下執行各種動作的預期回報的最大值。對於高維的輸入資料，顯然是不現實的，因為如果直接以原始資料作為狀態，維數太高，而且狀態數量太多。

一種解決方案是從高維資料中抽象出特徵，作為狀態，然後用強化學習建模，但這種做法很大程度上依賴於人工特徵的設計。如從畫面中提取出目標的位置、速度等資訊，也非常困難，這也是一個難題。

用一個函式來逼近價值函式或策略函式成為解決這個問題的一種思路，函式的輸入是原始的狀態資料，函式的輸出是價值函式值或策略函式值。

在有監督學習中，我們用神經網路來擬合分類或迴歸函式，同樣的，也可以用神經網路可來擬合強化學習中的價值函式和策略函式，這就是深度強化學習的基本思想。

將神經網路與強化學習進行結合並不是一個新的想法，早在1995年就有人進行了這一的嘗試。首先是TD-gammon演算法[4]，這是一種用強化學習玩西洋雙陸棋的方法，取得了比人類選手更好的成績。這種方法採用了與Q學習類似的策略，用多層感知器模型來逼近狀態價值函式（V函式而不是Q函式）。

對這個演算法感興趣的話，可以閱讀文獻[4]。然而，後來將這種演算法用於國際象棋，圍棋，西洋跳棋時，效果卻非常差。這使得人們認為TD-gammon演算法只是一個特例，而不具有通用性。

後面的分析表明，將Q學習這樣的無模型強化學習演算法（即不知道環境的狀態轉移概率，以及回報函式）與非線性價值函式逼近結合使用時會導致Q網路不收斂。即在訓練時Q網路無法收斂到Q函式的極大值。相比之下，用線性函式來逼近價值函式，會有更好的收斂性。對於收斂性問題，文獻[5]有詳細的分析與證明。

深度學習出現之後，將深度神經網路用於強化學習是一個很自然的想法。深度神經網路能夠實現端到端的學習，直接從影象，聲音等高維資料中學習得到有用的特徵，這比人工設計的特徵更為強大和通用。

在文獻[6]中，受限玻爾茲曼機被用於表示價值函式，在文獻[7]中，被用於表示策略函式。神經網路用於Q學習時不收斂的問題被gradient temporal-difference演算法部分解決。用非線性函式來學習一個固定的策略時，這些方法的收斂性是可以得到保證的，感興趣的可以閱讀文獻[]。用線性函式來近似價值函式，採用Q學習訓練，收斂性也可以得到保證，文獻[]對此有詳細的分析與論證。

文獻[8]提出了neural fitted Q-learning (NFQ)。這種方法優化方程上面定義的目標函式，採用 RPROP演算法更新Q網路的引數。需要強調的是，它採用了批量梯度下降法進行更新迭代，即每次進行梯度下降法迭代時使用了所有訓練樣本，因此單次迭代的計算量太大。這種方法需要反覆的對神經網路進行從頭開始的上百次的迭代，因此不適合訓練大規模的神經網路，因為效率太低。

NFQ也被用於現實世界中的控制任務[9]。以自動編碼器作為提取特徵的網路，直接接收視覺輸入訊號，然後將NFQ演算法作用於提取出的特徵表示。文獻[10]將Q學習與經驗回放機制進行整合，採用簡單的神經作為逼近器。這裡還是用低維的狀態向量作為神經網路的輸入，而不是高維的影象等原始資料。

深度學習取得了成功，在計算機視覺，語音識別領域，深度神經網路可以直接從場景資料如影象、聲音中提取出高層特徵，實現端到端的學習，而無需再人工設計特徵。一個很自然的想法是能否用深度學習來為強化學習的輸入原始資料進行建模。如果用神經王來近似Q函式，則網路的輸入值為狀態資料，如原始的遊戲畫面，輸出值為在當前狀態下執行各種動作所得到的最大預期回報。訓練樣本為狀態，目標Q函式值對。但是將深度學習用於強化學習將面臨幾個挑戰：

首先，深度學習需要大量的有標籤的訓練樣本，而在強化學習中，演算法要根據標量回報值進行學習，這個回報值往往是稀疏的，即不是執行每個動作都立刻能得到回報。例如對於打乒乓球這樣的遊戲，只有當自己或者對手失球時得分才會變化，此時才有回報，其他時刻沒有回報。回報值帶有噪聲，另外還具有延遲，當前時刻的動作所得到的回報在未來才能得到體現。例如，在下棋時，當前所走的一步的結果會延遲一段時間後才能得到體現。

第2個問題是有監督學習一般要求訓練樣本之間是相互獨立的，在強化學習中，經常遇到的是前後高度相關的狀態序列。在某個狀態下執行一個動作之後進入下一個狀態，前後兩個狀態之間存在著明顯的概率關係，不是獨立的。

第3個問題是在強化學習中，隨著學習到新的動作，樣本資料的概率分佈會發生變化，而在深度學習中，要求訓練樣本的概率分佈是固定的。

基於價值函式的演算法

基於價值函式的深度強化學習的典型代表是DQN（深度Q網路），由DeepMind公司在2013年提出，2015年其改進型發表在Nature上。這種方法用卷積神經網路擬合價值函式，一般是Q函式。網路的輸入為原始場景資料，如遊戲的畫面影象，輸出為在這種場景下執行各種動作時所能得到的Q函式的極大值。

文獻[11]第一次提出了DQN演算法，是深度強化學習真正意義上的開山之作。這篇文章用Atari遊戲對演算法進行了測試。演算法用深度卷積神經網路來擬合Q函式，這個網路稱為Q網路。網路的輸入為經過處理後的遊戲畫面（最近4幀遊戲畫面），輸出為在這種狀態下執行各種動作的Q函式值。網路結構如下圖所示：

損失函式用神經網路的輸出值與Q學習每次迭代時的更新值構造，是神經網路的輸出值與Q函式估計值之間的誤差，與Q學習中的更新項相同：

 

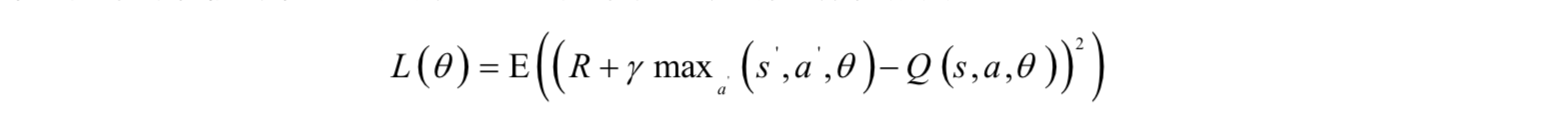
和Q學習類似，可以通過執行動作來生成樣本。實現時，給定一個狀態，用當前的神經網路進行預測，得到所有動作的Q函式，然後按照策略選擇一個動作執行，得到下一個狀態以及回報值，以此構造訓練樣本。

確定網路結構和損失函式之後，剩下的就是神經網路的訓練，與普通的有監督學習不同，這裡的訓練樣本是通過不停的執行動作而動態生成的。為了解決訓練樣本之間存在相關性，以及樣本的概率分佈不固定的問題，採用了經驗回放機制，具體做法是，先把執行動作構造的訓練樣本儲存到一個大的集合中，在訓練Q網路時每次從這個集合中隨機抽取出部分樣本作為訓練樣本，以此打破樣本之間的相關性。

訓練演算法的流程如下：

一旦訓練出了神經網路，便可以得到任何畫面下要執行的動作，這通過使用Q函式值和貪心策略來實現，從而完成遊戲的控制。

實驗結果證明了DQN的收斂性，作者對此也進行了細緻的分析。文章分析了遊戲片段的平均回報值，隨著迭代的進行，回報會升高，雖然有震盪。另外還分析了動作價值函式值，即Q函式的均值。同樣的，隨著迭代的進行會升高，雖然會震盪。

另外還在實驗中比較了DQN與其他各種演算法，以及人類選手的效能。參加比較的演算法有SARSA演算法，採用人工設計的特徵。Contingency演算法，採用和SARSA相同的方法，但是通過學習部分螢幕的表達增強了特徵，特徵提取採用影象處理方法如背景減除。人類的得分是人類玩兩小時的結果。在絕大部分遊戲上，DQN超過了之前最好的演算法，在部分遊戲上，甚至超過了人類玩家的水平。

DQN實現了端到端學習，無需人工提取狀態和特徵，整合了深度學習與強化學習，深度學習用於感知任務。可以解決複雜環境下的決策問題。方法具有通用性，可以用於各種不同的問題。

DQN在隨機嘗試執行動作，生成訓練樣本的過程中，需要用當前的Q網路來計算訓練樣本的標籤值，這存在著自身依賴：

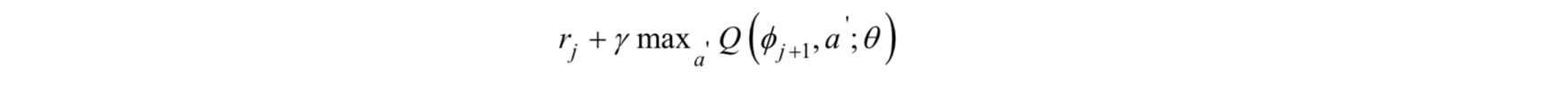
即Q值與Q學習的目標值r+γmaxa'Q(s',a')之間的相關性。為了解決此問題，文獻[12]對DQN進行了改進。它提出的演算法和2013年DQN主要的不同是計算目標值是使用了另外一個Q網路，兩個網路週期性的進行同步。

Q學習在第i次迭代時的損失函式為：

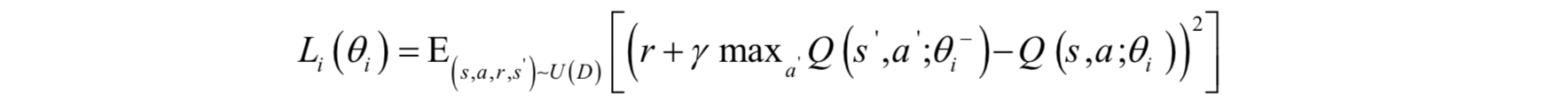
其中γ為折扣因子，θi為Q網路在第次迭代時的引數值，為第第次迭代時用於計算目標值的Q網路的引數值，這個神經網路稱為目標網路。目標網路與當前的Q網路分離開來，這是與2013年DQN最大的區別，當前Q網路的值在訓練時每次都迭代更新，而目標網路則週期性的從當前Q網路同步過來，每多次迭代執行一次拷貝。系統結構如下圖所示：

除了分析訓練演算法的收斂性、與其他演算法以及人類進行比較之外，文獻[12]還對DQN學習到的表達進行了分析，正是由它支撐了演算法在遊戲環境中的成功表現。這通過使用一種對高維資料進行視覺化的方法-t-SNE而實現。t-SNE可以將感知上相似的狀態通過DQN學習到的表達對映為相鄰的點。作者發現，對於有些畫面，t-SNE對DQN學習得到的表示的投影結果非常相近，這些遊戲畫面不相似，但Q函式值很相似，這意味著在這些畫面下要採用類似的動作。這與我們的觀點一致，神經網路可以從場景資料中學習得到支撐自適應行為的表示，即不同的場景下可能會使用相同的行為。
雖然DQN取得了成功，但還有很大的優化空間，此後DQN出現了大量改進型演算法，這些改進包括系統整體結構、訓練樣本的構造、神經網路結構等方面。

文獻[13]提出了Double DQN（DDQN）演算法。DDQN中有兩組不同的引數，和θ和θ-。θ用於選擇對應最大Q值的動作，θ-用於評估最優動作的Q值。這兩組引數將動作選擇和策略評估分離，降低了過高估計Q值的風險。DDQN 使用當前值網路的引數θ選擇最優動作，用目標值網路的引數θ-評估該最優動作。實驗結果證明，DDQN能更準確的估計Q函式值，使得訓練演算法和訓練得到的策略更為穩定。

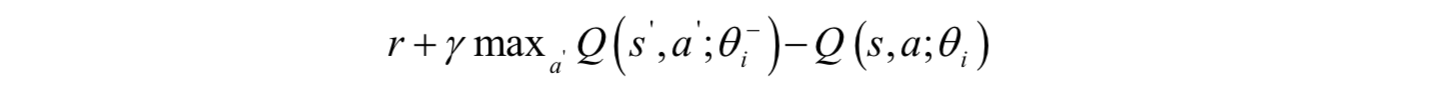
文獻[14]提出了基於優先順序取樣的DQN，是對經驗回放機制的改進。在之前的DQN中，經驗回放通過經驗池中的樣本等概率隨機抽樣來獲得每次迭代時的訓練樣本。顯然，這沒有利用每個樣本的重要性。文獻[14]的方法為經驗池中的每個樣本計算優先順序，增大有價值的訓練樣本在取樣時的概率。樣本的優先順序用時序差分演算法的誤差項進行構造，計算公式為：

這個值的絕對值越大，樣本在取樣時的概率越大。實驗結果證明這種演算法有更快的訓練速度，並且在執行時有更好的效果。

文獻[15]提出了基於競爭架構的 DQN。其主要改進是將CNN卷積層之後的全連線層替換為兩個分支，其中一個分支擬合狀態價值函式，另外一個分支擬合動作優勢函式。最後將兩個分支的輸出值相加，形成Q函式值。實驗表明，這種改進能夠更準確的估計價值函式值。

DQN中的深度神經網路是卷積神經網路，不具有長時間的記憶能力。為此，文獻[16]提出了一種整合了迴圈神經網路（RNN）的DQN演算法（DRQN）。這種方法在CNN的卷積層之後加入了迴圈層（LSTM單元），能夠記住之前的資訊。

參考文獻

[1] Sutton, R. & Barto, A. Reinforcement Learning: An Introduction (MIT Press, 1998).

[2] Richard Sutton. Learning to predict by the methods of temporal differences. Machine Learning. 3 (1): 9-44.1988.

[3] Christopher JCH Watkins and Peter Dayan. Q-learning. Machine learning, 8(3-4):279–292, 1992.

[4] Gerald Tesauro. Temporal difference learning and td-gammon. Communications of the ACM,

38(3):58–68, 1995.

[5] Tsitsiklis J N, Van R B. An analysis of temporal-difference learning with function approximation. IEEE Transactions on Automatic Control, 1997, 42(5): 674-690

[6] Brian Sallans and Geoffrey E. Hinton. Reinforcement learning with factored states and actions.

Journal of Machine Learning Research, 5:1063–1088, 2004.

[7] Nicolas Heess, David Silver, and Yee Whye Teh. Actor-critic reinforcement learning with

energy-based policies. In European Workshop on Reinforcement Learning, page 43, 2012.

[8] Riedmiller M. Neural fitted q iteration-first experiences with a data efficient neural reinforcement learning method. Proceedings of the Conference on Machine Learning. Berlin, German, 2005: 317-328

[9] Sascha Lange and Martin Riedmiller. Deep auto-encoder neural networks in reinforcement

learning. In Neural Networks (IJCNN), The 2010 International Joint Conference on, pages

1–8. IEEE, 2010.

[10] Long-Ji Lin. Reinforcement learning for robots using neural networks. Technical report, DTIC

Document, 1993.

[11] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou. Playing Atari with Deep Reinforcement Learning. NIPS 2013.

[12] Mnih, Volodymyr, et al. Human-level control through deep reinforcement learning. Nature. 518 (7540): 529-533, 2015.

[13] Van H V, Guez A, Silver D. Deep reinforcement learning with double q-learning. Proceedings of the AAAI Conference on Artificial Intelligence. Phoenix, USA, 2016: 2094-2100.

[14] Schaul T, Quan J, Antonoglou I, Silver D. Prioritized experience replay. Proceedings of the 4th International Conference on Learning Representations. San Juan, Puerto Rico, 2016:322-355.

[15] Wang Z, Freitas N D, Lanctot M. Dueling network architectures for deep reinforcement learning. Proceedings of the International Conference on Machine Learning. New York, USA, 2016: 1995-2003.

[16] Hausknecht M, Stone P. Deep recurrent q-learning for partially observable MDPs. arXiv preprint arXiv:1507.06527, 2015.