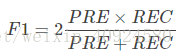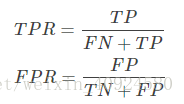練習總結 +sklearn引數選擇調優
比賽相關部分練習總結
df_train = pd.read_csv('C:/Users/zhangy/Desktop/kaggle_competition_feature_engineering/kaggle_bike_competition_train.csv') # print(train.shape) # print(train.apply(lambda x:sum(x.isnull()))) #檢視每一列缺失值的數量 df_train['month'] = pd.DatetimeIndex(df_train.datetime).month df_train['day'] = pd.DatetimeIndex(df_train.datetime).dayofweek df_train['hour'] = pd.DatetimeIndex(df_train.datetime).hour df_train_origin = df_train df_train=df_train.drop(['datetime'],axis=1) df_train_target = df_train['count'] #訓練集標籤 df_train_data = df_train.drop(['count'],axis=1) #訓練集資料 X_train,X_test,y_train,y_test=train_test_split(df_train_data,df_train_target,test_size=0.2,random_state=0)
# clf = RandomForestRegressor(n_estimators=100)
# clf.fit(X_train,y_train)
# print(clf.score(X_train,y_train))
# print(clf.score(X_test,y_test))
RandomForest:
sklearn.ensemble.RandomForestRegressor( n_estimators=10, criterion='mse', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features='auto', max_leaf_nodes=None, min_impurity_split=1e-07, bootstrap=True, oob_score=False, n_jobs=1, random_state=None, verbose=0, warm_start=False)
其中關於決策樹的引數:
criterion: “mse”來選擇最合適的節點。
splitter: ”best” or “random”(default=”best”)隨機選擇屬性還是選擇不純度最大的屬性,建議用預設。
max_features: 選擇最適屬性時劃分的特徵不能超過此值。
當為整數時,即最大特徵數;當為小數時,訓練集特徵數*小數;
if “auto”, then max_features=sqrt(n_features).
If “sqrt”, thenmax_features=sqrt(n_features).
If “log2”, thenmax_features=log2(n_features).
If None, then max_features=n_features.
max_depth: (default=None)設定樹的最大深度,預設為None,這樣建樹時,會使每一個葉節點只有一個類別,或是達到min_samples_split。
min_samples_split: 根據屬性劃分節點時,每個劃分最少的樣本數。
min_samples_leaf: 葉子節點最少的樣本數。
max_leaf_nodes: (default=None)葉子樹的最大樣本數。
min_weight_fraction_leaf: (default=0) 葉子節點所需要的最小權值
verbose: (default=0) 是否顯示任務程序
關於隨機森林特有的引數:
n_estimators=10: 決策樹的個數,越多越好,但是效能就會越差,至少100左右(具體數字忘記從哪裡來的了)可以達到可接受的效能和誤差率。
bootstrap=True: 是否有放回的取樣。
oob_score=False: oob(out of band,帶外)資料,即:在某次決策樹訓練中沒有被bootstrap選中的資料。多單個模型的引數訓練,我們知道可以用cross validation(cv)來進行,但是特別消耗時間,而且對於隨機森林這種情況也沒有大的必要,所以就用這個資料對決策樹模型進行驗證,算是一個簡單的交叉驗證。效能消耗小,但是效果不錯。
n_jobs=1: 並行job個數。這個在ensemble演算法中非常重要,尤其是bagging(而非boosting,因為boosting的每次迭代之間有影響,所以很難進行並行化),因為可以並行從而提高效能。1=不併行;n:n個並行;-1:CPU有多少core,就啟動多少job
warm_start=False: 熱啟動,決定是否使用上次呼叫該類的結果然後增加新的。
class_weight=None: 各個label的權重。
進行預測可以有幾種形式:
predict_proba(x): 給出帶有概率值的結果。每個點在所有label的概率和為1.
predict(x): 直接給出預測結果。內部還是呼叫的predict_proba(),根據概率的結果看哪個型別的預測值最高就是哪個型別。
predict_log_proba(x): 和predict_proba基本上一樣,只是把結果給做了log()處理。
# clf = svm.SVC(kernel='rbf',C=10,gamma=0.001,probability=True)
# clf.fit(X_train,y_train)
#
# print(clf.score(X_train,y_train))
# print(clf.score(X_test,y_test))
SVM:
sklearn.svm.SVC(C=1.0, kernel=‘rbf’, degree=3, gamma=‘auto’, coef0=0.0, shrinking=True, probability=False,
tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=None,random_state=None)
引數:
l C:C-SVC的懲罰引數C?預設值是1.0
C越大,相當於懲罰鬆弛變數,希望鬆弛變數接近0,即對誤分類的懲罰增大,趨向於對訓練集全分對的情況,這樣對訓練集測試時準確率很高,但泛化能力弱。C值小,對誤分類的懲罰減小,允許容錯,將他們當成噪聲點,泛化能力較強。
l kernel :核函式,預設是rbf,可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’
0 – 線性:u’v
1 – 多項式:(gamma*u’*v + coef0)^degree
2 – RBF函式:exp(-gamma|u-v|^2)
3 –sigmoid:tanh(gamma*u’*v + coef0)
l degree :多項式poly函式的維度,預設是3,選擇其他核函式時會被忽略。
l gamma : ‘rbf’,‘poly’ 和‘sigmoid’的核函式引數。預設是’auto’,則會選擇1/n_features
l coef0 :核函式的常數項。對於‘poly’和 ‘sigmoid’有用。
l probability :是否採用概率估計?.預設為False
l shrinking :是否採用shrinking heuristic方法,預設為true
l tol :停止訓練的誤差值大小,預設為1e-3
l cache_size :核函式cache快取大小,預設為200
l class_weight :類別的權重,字典形式傳遞。設定第幾類的引數C為weight*C(C-SVC中的C)
l verbose :允許冗餘輸出?
l max_iter :最大迭代次數。-1為無限制。
l decision_function_shape :‘ovo’, ‘ovr’ or None, default=None3
l random_state :資料洗牌時的種子值,int值
主要調節的引數有:C、kernel、degree、gamma、coef0
tuned_parameters = [{'n_estimators':[10,100,500]}]
scores = ['r2']
for score in scores:
clf = GridSearchCV(RandomForestRegressor(),tuned_parameters,cv=5,scoring=score)
clf.fit(X_train,y_train)
print("最佳引數為:")
print(clf.best_params_)
print("得分分別為:")
for params, mean_score, scores in clf.grid_scores_:
print("%0.3f (+/-%0.03f) for %r"% (mean_score, scores.std()/2, params))
GridSearchCV:
sklearn.model_selection.GridSearchCV(estimator, param_grid, scoring=None, fit_params=None, n_jobs=1, iid=True, refit=True, cv=None, verbose=0, pre_dispatch=‘2*n_jobs’, error_score=’raise’, return_train_score=’warn’)
estimator —— 模型
param_grid —— dict or list of dictionaries
scoring ---- 評分函式
fit_params --- dict, optional
n_jobs ------並行任務個數,int, default=1
pre_dispatch ------ int, or string, optional ‘2*n_jobs’
iid ----- boolean, default=True
cv ----- int, 交叉驗證,預設3
refit ---- boolean, or string, default=True
verbose ----- integer
error_score ------ ‘raise’ (default) or numeric
總結一些特徵檢視處理小技巧
print(train.apply(lambda x:sum(x.isnull()))) #檢視每列特徵缺失值個數
print(train['grade'].value_counts()) #檢視某列資料不同值的個數
print(train['int_rate'].unique()) #檢視某特徵中只有一個值得項
train.drop(['id','member_id'],axis=1,inplace=True) #刪掉資料集中的某些列
train.boxplot(column=['open_acc'],return_type='axes') #繪製某一列特徵的箱體圖
temp = pd.DatetimeIndex(train['datetime'])
train['date'] = temp.date
train['time'] = temp.time #2011/1/1 2:00:00原特徵,現在講時間和日期分開
train['hour'] = pd.to_datetime(train.time, format="%H:%M:%S")
train['hour'] = pd.Index(train['hour']).hour #再單獨把hour拿出來
train['dayofweek'] = pd.DatetimeIndex(train.date).dayofweek #把資料轉換為周幾
train['dateDays'] = (train.date - train.date[0]).astype('timedelta64[D]') #表示距離第一套的時長
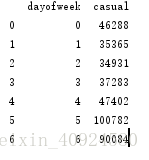
byday = train.groupby('dayofweek')
print(byday['casual'].sum().reset_index()) #統計一週每天‘casual’特徵的情況
train['Saturday']=0
train.Saturday[train.dayofweek==5]='a'
train['Sunday']=0
train.Sunday[train.dayofweek==6]='b' #單獨去除某一天作為特徵,並賦值(任意)
train['Saturday']=0
train.Saturday[train.dayofweek==5]='a'
train['Sunday']=0
train.Sunday[train.dayofweek==6]='b' #單獨去除某一天作為特徵,並賦值(任意)
dataRel = train.drop(['datetime', 'count','date','time','dayofweek'], axis=1) #刪除某些列
對於pandas的dataframe我們有方法/函式可以直接轉成python中的dict。另外,在這裡我們要對離散值和連續值特徵區分一下了,以便之後分開做不同的特徵處理
featureConCols = ['temp','atemp','humidity','windspeed','dateDays','hour']
dataFeatureCon = dataRel[featureConCols]
dataFeatureCon = dataFeatureCon.fillna( 'NA' ) #in case I missed any
X_dictCon = dataFeatureCon.T.to_dict().values()
把離散值的屬性放到另外一個dict中
featureCatCols = ['season','holiday','workingday','weather','Saturday', 'Sunday']
dataFeatureCat = dataRel[featureCatCols]
dataFeatureCat = dataFeatureCat.fillna( 'NA' ) #in case I missed any
X_dictCat = dataFeatureCat.T.to_dict().values()
向量化特徵
vec = DictVectorizer(sparse = False)
X_vec_con = vec.fit_transform(X_dictCon)
X_vec_cat = vec.fit_transform(X_dictCat)
對連續值屬性做一些處理,最基本的當然是標準化,讓連續值屬性處理過後均值為0,方差為1。
from sklearn import preprocessing
# 標準化連續值資料
scaler = preprocessing.StandardScaler().fit(X_vec_con)
X_vec_con = scaler.transform(X_vec_con) #標準化連續值向量
類別特徵編碼,最常用的當然是one-hot編碼咯,比如顏色 紅、藍、黃 會被編碼為[1, 0, 0],[0, 1, 0],[0, 0, 1]
from sklearn import preprocessing
# one-hot編碼
enc = preprocessing.OneHotEncoder()
enc.fit(X_vec_cat)
X_vec_cat = enc.transform(X_vec_cat).toarray()
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
y = le.fit_transform(y) # 把字串標籤轉換為整數,惡性-1,良性-0 標籤編碼
k-fold交叉驗證:
1自己手寫!!
from sklearn.cross_validation import StratifiedKFold
import numpy as np
scores = []
kfold = StratifiedKFold(y=y_train, n_folds=10, random_state=1) # n_folds引數設定為10份
for train_index, test_index in kfold:
pipe_lr.fit(X_train[train_index], y_train[train_index])
score = clf.score(X_train[test_index], y_train[test_index])
scores.append(score)
print('類別分佈: %s, 準確度: %.3f' % (np.bincount(y_train[train_index]), score))
2、sklearn
from sklearn.cross_validation import cross_val_score
scores = cross_val_score(estimator=clf, X=X_train, y=y_train, cv=10, n_jobs=1)
F-score:
from sklearn.metrics import confusion_matrix
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
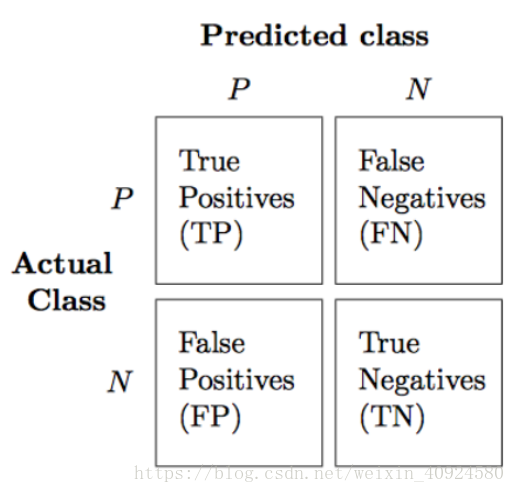
confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)
confmat即為:
在類別很不平衡的機器學習系統中,我們通常用precision(PRE)和recall(REC)來度量模型的效能,下面我給出它們的公式:
在實際中,我們通常結合兩者,組成F1-score:
在介紹ROC曲線前,我先給出true positive rate(TPR)和false positive rate(FPR)的定義:
from sklearn.metrics import roc_curve, auc
from scipy import interp
X_train2 = X_train[:, [4, 14]]
cv = StratifiedKFold(y_train, n_folds=3, random_state=1)
fig = plt.figure()
mean_tpr = 0.0
mean_fpr = np.linspace(0, 1, 100)
all_tpr = []
# plot每個fold的ROC曲線,這裡fold的數量為3,被StratifiedKFold指定
for i, (train, test) in enumerate(cv):
# 返回預測的每個類別(這裡為0或1)的概率
probas = pipe_lr.fit(X_train2[train], y_train[train]).predict_proba(X_train2[test])
fpr, tpr, thresholds = roc_curve(y_train[test], probas[:, 1], pos_label=1)
mean_tpr += interp(mean_fpr, fpr, tpr)
mean_tpr[0] = 0.0
roc_auc = auc(fpr, tpr)
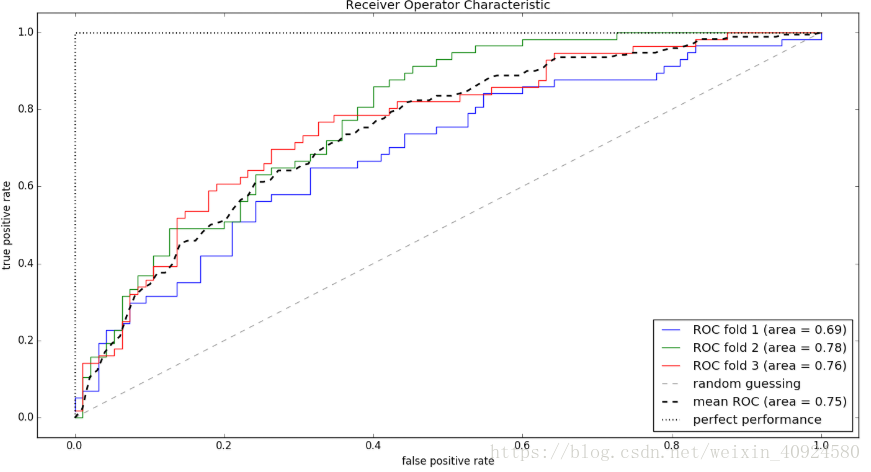
plt.plot(fpr, tpr, linewidth=1, label='ROC fold %d (area = %0.2f)' % (i+1, roc_auc))
# plot random guessing line
plt.plot([0, 1], [0, 1], linestyle='--', color=(0.6, 0.6, 0.6), label='random guessing')
mean_tpr /= len(cv)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
plt.plot(mean_fpr, mean_tpr, 'k--', label='mean ROC (area = %0.2f)' % mean_auc, lw=2)
# plot perfect performance line
plt.plot([0, 0, 1], [0, 1, 1], lw=2, linestyle=':', color='black', label='perfect performance')
# 設定x,y座標範圍
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('false positive rate')
plt.ylabel('true positive rate')
plt.title('Receiver Operator Characteristic')
plt.legend(loc="lower right")
plt.show()
roc官方文件:
http://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_curve.html