1.計數排序：Counting Sort

計數排序是一個非基於比較的排序演算法，該演算法於1954年由 Harold H. Seward 提出，它的優勢在於在對於較小範圍內的整數排序。它的複雜度為Ο(n+k)（其中k是待排序數的最大值），快於任何比較排序演算法，缺點就是非常消耗空間。很明顯，如果而且當O(k)>O(n*log(n))的時候其效率反而不如基於比較的排序，比如堆排序和歸併排序和快速排序。

演算法原理：  基本思想是對於給定的輸入序列中的每一個元素x，確定該序列中值小於x的元素的個數。一旦有了這個資訊，就可以將x直接存放到最終的輸出序列的正確位置上。例如，如果輸入序列中只有17個元素的值小於x的值，則x可以直接存放在輸出序列的第18個位置上。當然，如果有多個元素具有相同的值時，我們不能將這些元素放在輸出序列的同一個位置上，在程式碼中作適當的修改即可。

用待排序的數作為計數陣列的下標，統計每個數字的個數。然後依次輸出即可得到有序序列。

演算法步驟：  （1）找出待排序的陣列中最大的元素；  （2）統計陣列中每個值為i的元素出現的次數，存入陣列C的第i項；  （3）對所有的計數累加（從C中的第一個元素開始，每一項和前一項相加）；  （4）反向填充目標陣列：將每個元素i放在新陣列的第C(i)項，每放一個元素就將C(i)減去1。

時間複雜度：Ο(n+k)。

空間複雜度：Ο(k)。

要求：待排序數中最大數值不能太大。最大值確定並且不大，必須是正整數。 

穩定性：穩定。

計數排序需要佔用大量空間，它僅適用於資料比較集中的情況。比如 [0~100]，[10000~19999] 這樣的資料。

計數排序的基本思想是：對每一個輸入的元素arr[i]，確定小於 arr[i] 的元素個數。 所以可以直接把 arr[i] 放到它輸出陣列中的位置上。假設有5個數小於 arr[i]，所以 arr[i] 應該放在陣列的第6個位置上。

計數排序用到一個額外的計數陣列C，根據陣列C來將原陣列A中的元素排到正確的位置。

　　通俗地理解，例如有10個年齡不同的人，假如統計出有8個人的年齡不比小明大（即小於等於小明的年齡，這裡也包括了小明），那麼小明的年齡就排在第8位，通過這種思想可以確定每個人的位置，也就排好了序。當然，年齡一樣時需要特殊處理（保證穩定性）：通過反向填充目標陣列，填充完畢後將對應的數字統計遞減，可以確保計數排序的穩定性。

計數排序屬於線性排序，它的時間複雜度遠遠大於常用的比較排序。（計數是O(n)，而比較排序不會超過O(nlog2nJ)）。

其實計數排序大部分很好理解的，唯一理解起來很蛋疼的是為了保證演算法穩定性而做的資料累加，大家聽我說說就知道了：

1、首先，先取出要排序陣列的最大值，假如我們的陣列是int[] arrayData = { 2, 4, 1, 5, 6, 7, 4, 65, 42 };，那麼最大值就是65.（程式碼17-21行就是在查詢最大值）

2、然後建立一個計數陣列，計數陣列的長度就是我們的待排序陣列長度+1。即65+1=66。計數陣列的作用就是用來儲存待排序陣列中，數字出現的頻次。 例如，4出現了兩次，那麼計數陣列arrayCount[4]=2。 OK，現在應該明白為什麼計數陣列長度為什麼是66而不是65了吧？ 因為為了儲存0

    然後再建立一個儲存返回結果的陣列，陣列長度與我們的原始資料長度是相同的。（24和26行）

3、進行計數（程式碼29至31行）

4、將計數陣列進行數量累計，即arrayCount[i]+=arrayCount[i-1]（程式碼35行至程式碼37行）。　

　  目的是為了資料的穩定性， 這塊我其實看了許久才看懂的…再次證明我的資質真的很差勁。 我來盡力解釋一下：

     其實這個與後邊那步結合著看理解起來應該更容易些。

     例如我們計數陣列分別是 1 2 1 2 1 的話，那麼就代表0出現了一次，1出現了兩次，2出現了一次，3出現了兩次。

　　這個是很容易理解的。 那我們再換個角度來看這個問題。

　　我們可以根據這個計數陣列得到每個數字出現的索引位置，即數字0出現的位置是索引0，數字1出現的問題是索引1，2；數字2出現的位置是索引3，數字4出現的位置是索引4，5。。。。

　　OK，大家可以看到，這個索引位置是累加的，所以我們需要arrayCount[i]+=arrayCount[i-1]來儲存每個數字的索引最大值。 這樣為了後邊的輸出

5、最後，把原始資料從後往前輸出；然後每個數字都能找到計數器的最後實現索引。  然後將數字儲存在實際索引的結果陣列中。 然後計數陣列的索引--， 結果就出來了。

PS:計數排序其實是特別吃記憶體的

時間複雜度：

O(n+k)  

請對照下方程式碼：因為有n的迴圈，也有k的迴圈，所以時間複雜度是n+k

空間複雜度：

O(n+k)  

請對照下方程式碼：需要一個k+1長度的計數陣列，需要一個n長度的結果陣列，所以空間複雜度是n+k

    public static void main(String[] args) {

        int[] arrayData = { 2, 3, 1, 5, 6, 7, 4, 65, 42 };

        int[] arrayResult = CountintSort(arrayData);

    }

public static int[] CountintSort(int[] arrayData) {
    int maxNum = 0;
    // 取出最大值
    for (int i : arrayData) {
        if (i > maxNum) {
            maxNum = i;
        }
    }

    // 計數陣列
    int[] arrayCount = new int[maxNum + 1];
    // 結果陣列
    int[] arrayResult = new int[arrayData.length];

    // 開始計數
    for (int i : arrayData) {
        arrayCount[i]++;
    }

    // 對於計數陣列進行 i=i+(i-1)
    // 目的是為了保證資料的穩定性
    for (int i = 1; i < arrayCount.length; i++) {
        arrayCount[i] = arrayCount[i] + arrayCount[i - 1];
    }

    for (int i = arrayData.length - 1; i >= 0; i--) {
        arrayResult[arrayCount[arrayData[i]] - 1] = arrayData[i];
        arrayCount[arrayData[i]]--;
    }

    return arrayResult;

}

演算法分析

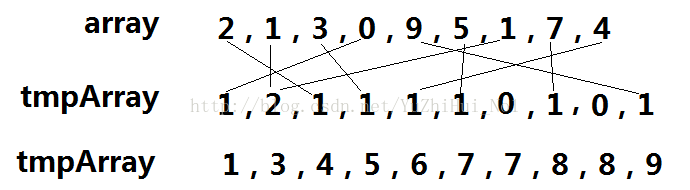
        主要思想：根據array陣列元素的值進行排序，然後統計大於某元素的元素個數，最後就可以得到某元素的合適位置；比如：array[4] = 9；統計下小於array[4]的元素個數為：8；所以array[4] = 9 應該放在元素的第8個位置；

        主要步驟：

       1、根據array陣列，把相應的元素值對應到tmpArray的位置上；

2、然後根據tmpArray陣列元素進行統計大於array陣列各個元素的個數；

     3、最後根據上一步統計到的元素，為array元素找到合適的位置，暫時存放到tmp陣列中；

        如下圖所示：array 是待排序的陣列；tmpArray 是相當於桶的概念； tmp 是臨時陣列，儲存array排好序的陣列；

        注意：計數排序對輸入元素有嚴格要求，因為array元素值被用來當作tmpArray陣列的下標，所以如果array的元素值為100的話，那麼tmpArray陣列就要申請101（包括0，也就是 mix - min + 1）。

時間複雜度

        時間複雜度可以很好的看出了就是：O( n )；

空間複雜度

        空間複雜度也可以很好的看出來：O( n )；

總結

        計數排序的時間複雜度和空間複雜度都是非常有效的，但是該演算法對輸入的元素有限制要求，所以並不是所有的排序都使用該演算法；最好的是0～9之間的數值差不會很大的資料元素間比較；有人會說這個沒多大用，但是在後面的基數排序中會看到，這可以算是基數排序中的一個基礎；