1.計數排序：Counting Sort

計數排序是一個非基於比較的排序演算法，該演算法於1954年由 Harold H. Seward 提出，它的優勢在於在對於較小範圍內的整數排序。它的複雜度為Ο(n+k)（其中k是待排序數的最大值），快於任何比較排序演算法，缺點就是非常消耗空間。很明顯，如果而且當O(k)>O(n*log(n))的時候其效率反而不如基於比較的排序，比如堆排序和歸併排序和快速排序。

演算法原理： 
基本思想是對於給定的輸入序列中的每一個元素x，確定該序列中值小於x的元素的個數。一旦有了這個資訊，就可以將x直接存放到最終的輸出序列的正確位置上。例如，如果輸入序列中只有17個元素的值小於x的值，則x可以直接存放在輸出序列的第18個位置上。當然，如果有多個元素具有相同的值時，我們不能將這些元素放在輸出序列的同一個位置上，在程式碼中作適當的修改即可。

用待排序的數作為計數陣列的下標，統計每個數字的個數。然後依次輸出即可得到有序序列。

演算法步驟： 
（1）找出待排序的陣列中最大的元素； 
（2）統計陣列中每個值為i的元素出現的次數，存入陣列C的第i項； 
（3）對所有的計數累加（從C中的第一個元素開始，每一項和前一項相加）； 
（4）反向填充目標陣列：將每個元素i放在新陣列的第C(i)項，每放一個元素就將C(i)減去1。

時間複雜度：Ο(n+k)。

空間複雜度：Ο(k)。

要求：待排序數中最大數值不能太大。最大值確定並且不大，必須是正整數。 

穩定性：穩定。

 

計數排序需要佔用大量空間，它僅適用於資料比較集中的情況。比如 [0~100]，[10000~19999] 這樣的資料。

計數排序的基本思想是：對每一個輸入的元素arr[i]，確定小於 arr[i] 的元素個數。
所以可以直接把 arr[i] 放到它輸出陣列中的位置上。假設有5個數小於 arr[i]，所以 arr[i] 應該放在陣列的第6個位置上。

 

計數排序用到一個額外的計數陣列C，根據陣列C來將原陣列A中的元素排到正確的位置。

　　通俗地理解，例如有10個年齡不同的人，假如統計出有8個人的年齡不比小明大（即小於等於小明的年齡，這裡也包括了小明），那麼小明的年齡就排在第8位，通過這種思想可以確定每個人的位置，也就排好了序。當然，年齡一樣時需要特殊處理（保證穩定性）：通過反向填充目標陣列，填充完畢後將對應的數字統計遞減，可以確保計數排序的穩定性。

 

計數排序屬於線性排序，它的時間複雜度遠遠大於常用的比較排序。（計數是O(n)，而比較排序不會超過O(nlog2nJ)）。

其實計數排序大部分很好理解的，唯一理解起來很蛋疼的是為了保證演算法穩定性而做的資料累加，大家聽我說說就知道了：

1、首先，先取出要排序陣列的最大值，假如我們的陣列是int[] arrayData = { 2, 4, 1, 5, 6, 7, 4, 65, 42 };，那麼最大值就是65.（程式碼17-21行就是在查詢最大值）

2、然後建立一個計數陣列，計數陣列的長度就是我們的待排序陣列長度+1。即65+1=66。計數陣列的作用就是用來儲存待排序陣列中，數字出現的頻次。 例如，4出現了兩次，那麼計數陣列arrayCount[4]=2。 OK，現在應該明白為什麼計數陣列長度為什麼是66而不是65了吧？ 因為為了儲存0

    然後再建立一個儲存返回結果的陣列，陣列長度與我們的原始資料長度是相同的。（24和26行）

3、進行計數（程式碼29至31行）

4、將計數陣列進行數量累計，即arrayCount[i]+=arrayCount[i-1]（程式碼35行至程式碼37行）。　

　  目的是為了資料的穩定性， 這塊我其實看了許久才看懂的…再次證明我的資質真的很差勁。 我來盡力解釋一下：

     其實這個與後邊那步結合著看理解起來應該更容易些。

     例如我們計數陣列分別是 1 2 1 2 1 的話，那麼就代表0出現了一次，1出現了兩次，2出現了一次，3出現了兩次。

　　這個是很容易理解的。 那我們再換個角度來看這個問題。

　　我們可以根據這個計數陣列得到每個數字出現的索引位置，即數字0出現的位置是索引0，數字1出現的問題是索引1，2；數字2出現的位置是索引3，數字4出現的位置是索引4，5。。。。

　　OK，大家可以看到，這個索引位置是累加的，所以我們需要arrayCount[i]+=arrayCount[i-1]來儲存每個數字的索引最大值。 這樣為了後邊的輸出

5、最後，把原始資料從後往前輸出；然後每個數字都能找到計數器的最後實現索引。  然後將數字儲存在實際索引的結果陣列中。 然後計數陣列的索引--， 結果就出來了。

PS:計數排序其實是特別吃記憶體的

 

時間複雜度：

O(n+k)  

請對照下方程式碼：因為有n的迴圈，也有k的迴圈，所以時間複雜度是n+k

空間複雜度：

O(n+k)  

請對照下方程式碼：需要一個k+1長度的計數陣列，需要一個n長度的結果陣列，所以空間複雜度是n+k

    public static void main(String[] args) {

        int[] arrayData = { 2, 3, 1, 5, 6, 7, 4, 65, 42 };

        int[] arrayResult = CountintSort(arrayData);

    }

public static int[] CountintSort(int[] arrayData) {
    int maxNum = 0;
    // 取出最大值
    for (int i : arrayData) {
        if (i > maxNum) {
            maxNum = i;
        }
    }

    // 計數陣列
    int[] arrayCount = new int[maxNum + 1];
    // 結果陣列
    int[] arrayResult = new int[arrayData.length];

    // 開始計數
    for (int i : arrayData) {
        arrayCount[i]++;
    }

    // 對於計數陣列進行 i=i+(i-1)
    // 目的是為了保證資料的穩定性
    for (int i = 1; i < arrayCount.length; i++) {
        arrayCount[i] = arrayCount[i] + arrayCount[i - 1];
    }

    for (int i = arrayData.length - 1; i >= 0; i--) {
        arrayResult[arrayCount[arrayData[i]] - 1] = arrayData[i];
        arrayCount[arrayData[i]]--;
    }

    return arrayResult;

}

 

演算法分析

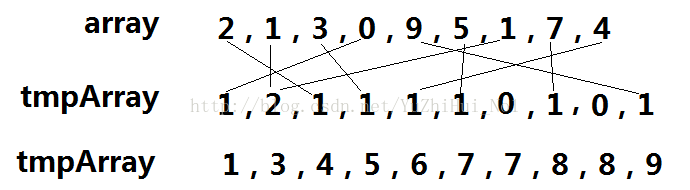
        主要思想：根據array陣列元素的值進行排序，然後統計大於某元素的元素個數，最後就可以得到某元素的合適位置；比如：array[4] = 9；統計下小於array[4]的元素個數為：8；所以array[4] = 9 應該放在元素的第8個位置；

        主要步驟：

       1、根據array陣列，把相應的元素值對應到tmpArray的位置上；

     2、然後根據tmpArray陣列元素進行統計大於array陣列各個元素的個數；

     3、最後根據上一步統計到的元素，為array元素找到合適的位置，暫時存放到tmp陣列中；

 

        如下圖所示：array 是待排序的陣列；tmpArray 是相當於桶的概念； tmp 是臨時陣列，儲存array排好序的陣列；

        

        注意：計數排序對輸入元素有嚴格要求，因為array元素值被用來當作tmpArray陣列的下標，所以如果array的元素值為100的話，那麼tmpArray陣列就要申請101（包括0，也就是 mix - min + 1）。

 

 

時間複雜度

        時間複雜度可以很好的看出了就是：O( n )；

 

空間複雜度

        空間複雜度也可以很好的看出來：O( n )；

 

總結

        計數排序的時間複雜度和空間複雜度都是非常有效的，但是該演算法對輸入的元素有限制要求，所以並不是所有的排序都使用該演算法；最好的是0～9之間的數值差不會很大的資料元素間比較；有人會說這個沒多大用，但是在後面的基數排序中會看到，這可以算是基數排序中的一個基礎；

 

 

 

 

基數排序(Radix Sort)

 

　　基數排序的發明可以追溯到1887年赫爾曼·何樂禮在打孔卡片製表機上的貢獻。它是這樣實現的：將所有待比較正整數統一為同樣的數位長度，數位較短的數前面補零。然後，從最低位開始進行基數為10的計數排序，一直到最高位計數排序完後，數列就變成一個有序序列（利用了計數排序的穩定性）。

        基數排序的時間複雜度是O(n * dn)，其中n是待排序元素個數，dn是數字位數。這個時間複雜度不一定優於O(n log n)，dn的大小取決於數字位的選擇（比如位元位數），和待排序資料所屬資料型別的全集的大小；dn決定了進行多少輪處理，而n是每輪處理的運算元目。

　　如果考慮和比較排序進行對照，基數排序的形式複雜度雖然不一定更小，但由於不進行比較，因此其基本操作的代價較小，而且如果適當的選擇基數，dn一般不大於log n，所以基數排序一般要快過基於比較的排序，比如快速排序。由於整數也可以表達字串（比如名字或日期）和特定格式的浮點數，所以基數排序並不是只能用於整數排序。

 

基數排序已經不再是一種常規的排序方式，它更多地像一種排序方法的應用，基數排序必須依賴於另外的排序方法。基數排序的總體思路就是將待排序資料拆分成多個關鍵字進行排序，也就是說，基數排序的實質是多關鍵字排序。

如果按照習慣思維，會先比較百位，百位大的資料大，百位相同的再比較十位，十位大的資料大；最後再比較個位。人得習慣思維是最高位優先方式。但一旦這樣，當開始比較十位時，程式還需要判斷它們的百位是否相同--這就認為地增加了難度，計算機通常會選擇最低位優先法。

基數排序方法對任一子關鍵字排序時必須藉助於另一種排序方法，而且這種排序方法必須是穩定的。對於多關鍵字拆分出來的子關鍵字，它們一定位於0-9這個可列舉的範圍內，這個範圍不大，因此用桶式排序效率非常好。對於多關鍵字排序來說，程式將待排資料拆分成多個子關鍵字後，對子關鍵字排序既可以使用桶式排序，也可以使用任何一種穩定的排序方法。

 

基數排序（radix sort）屬於“分配式排序”（distribution sort），又稱“桶子法”（bucket sort）或bin sort，顧名思義，它是透過鍵值的部份資訊，將要排序的元素分配至某些“桶”中，藉以達到排序的作用，基數排序法是屬於穩定性的排序，其時間複雜度為O (nlog(r)m)，其中r為所採取的基數，而m為堆數，在某些時候，基數排序法的效率高於其它的穩定性排序法。

 

演算法分析

 

     主要思想：

        基數排序的實現雖然有很多，但是基本思想就是把元素從個位排好序，然後再從十位排好序，，，，一直到元素中最大數的最高位排好序，那麼整個元素就排好序了。

                比如：2，22，31，1221，90，85，105

        個位排序：90，31，1221，2，22，85，105

        十位排序：2，105，1221，22，31，85，90

        百位排序：2，22，31，85，90，105，1221

        千位排序：2，22，31，85，90，105，1221

         注意：每次排序都是在上次排序的基礎上進行排序的，也就是說此次排序的位數上他們相對時，就不移動元素（即順序引數上一個位數的排序順序）

 

    主要步驟：

        1、把所有元素都分配到相應的桶中

       2、把所有桶中的元素都集合起來放回到陣列中

       3、依次迴圈上面兩步，迴圈次數為最大元素最高位數

 

    程式碼分析：

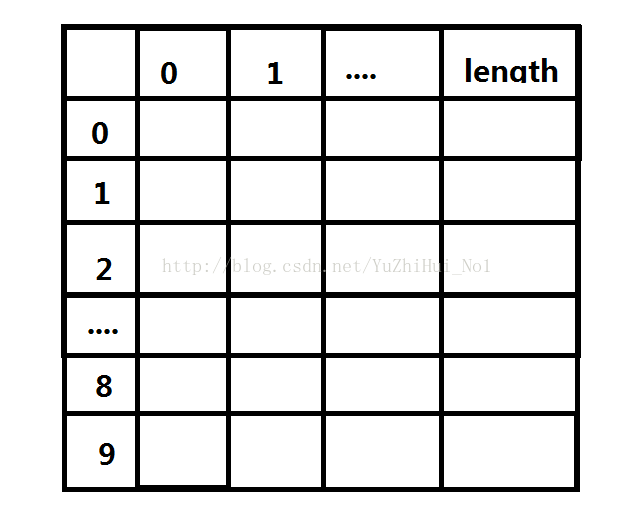
        參考下圖

     1、豎  0～9：表示桶個數（每個位數上的數字都在0到9之間）；

     2、行 0～length：0 表示在某個桶內有多少個元素；

     3、比如：所有元素中個位為5的有兩個元素，5 ， 95；那麼在下圖中存放，分別是：（5，0） = 2；（5，1） = 5；（5，2）= 95；

 

基數排序是基於計數排序的，所以看這個之前要先看一下計數排序對於理解基數排序是很有幫助的（發現計數和基數的音節幾乎一致啊）。

所謂基數排序，其實就是分別對數字的個位，十位，百位，百位。。。。分別進行計數排序。

當然可以從個位往上進行計數排序，也可以從高位往個數計數排序，這裡我們使用個位往上計數排序的方法。

 

先從與計數排序的區別說起吧，區別在於計數排序是直接對數字進行排序。而基數排序是分別對個位，十位，百位。。。進行排序的。

然後，每個位數中，都有0至9共10個數字（即個數時，其實就是10個數字做排序；十數時，其實也是對10個數字做排序），接著我們對每個數字中的數字進行計數排序（好繞口，意思就是說，當進行個數排序時，個位為1時，所以個位為1的數字進行計排，例如11，21，31，221，411等等）。

所以我們申請的是二維陣列int[][] radixBucket = new int[10][length]; （程式碼27行）  第一維的10儲存的就是我們每次都是對10個數分別進行計排。第二維儲存的就是對應的要排序的數字啦  

同時，因為我們要保證數字的穩定性，當我們把低位的數字進行計排後，要把低位數字輸出至原始陣列中，然後再進行高位排序。

 

public class RadixSort {
    public static void main(String[] args) {
        int[] arrayData = { 2, 3, 1, 5, 6, 7, 4, 65, 42 };
        RadixSortMethod(arrayData, 100);
        for (int integer : arrayData) {
            System.out.print(integer);
            System.out.print(" ");
        }
    }

    /*
     * arrayData - 要排序的資料 height - 要排序的步長 如果100，則只排序個位十位
     */
    public static void RadixSortMethod(int[] arrayData, int height) {
        int maxNum = 0; // 最大值，用於儲存桶資料臨時陣列空間大小
        for (int data : arrayData) {
            if (data > maxNum) {
                maxNum = data;
            }
        }

        int step = 1;
        int length = arrayData.length;
        int[][] radixBucket = new int[10][length]; // 二維陣列，排序的容器
        int[] arrayTemp = new int[maxNum + 1]; // 這個是每個桶中的數字個數
        int num;
        int index = 0;
        while (step < height) {
            for (int data : arrayData) {
                // 當step=1時統計個數，這時取出個位的數字。
                // 當step=10時，統計十數，這時取出十位的數字
                num = data / step % 10;
                radixBucket[num][arrayTemp[num]] = data;
                arrayTemp[num]++;
            }

            for (int i = 0; i < 10; i++) {
                if (arrayTemp.length > i && arrayTemp[i] != 0) {
                    for (int j = 0; j < arrayTemp[i]; j++) {
                        arrayData[index] = radixBucket[i][j];
                        index++;
                    }
                    arrayTemp[i] = 0; // 將當前數字個數重置為0，用於下次的統計
                }
            }

            step *= 10;
            index = 0;
        }
    }
}

 

時間複雜度：

假設步長是s,待排序陣列長度是n,數字最大值是m

那麼時間複雜度就是O(s(n+(10*m)))=O(s(m+n))

 

空間複雜度：

待排序陣列長度是n,數字最大值是m。

那麼空間複雜度就是O(10*n+(m+1))=O(m+n)

 

穩定性：是穩定的

 

應用場景：

針對最大值相對比較小的正整數。

 

時間複雜度

        該演算法所花的時間基本是在把元素分配到桶裡和把元素從桶裡串起來；把元素分配到桶裡：迴圈 length 次；

       把元素從桶裡串起來：這個計算有點麻煩，看似兩個迴圈，其實第二迴圈是根據桶裡面的元素而定的，可以表示為：k×buckerCount；其中 k 表示某個桶中的元素個數，buckerCount  則表示存放元素的桶個數；

       有幾種特殊情況：

       第一、所有的元素都存放在一個桶內：k = length，buckerCount = 1；

       第二、所有的元素平均分配到每個桶中：k = length/ bukerCount，buckerCount = 10；（這裡已經固定了10個桶）

       所以平均情況下收集部分所花的時間為：length （也就是元素長度 n）

 

       綜上所述：

       時間複雜度為：posCount * (length  + length) ；其中 posCount 為陣列中最大元素的最高位數；簡化下得：O( k*n ) ；其中k為常數，n為元素個數；

 

空間複雜度

        該演算法的空間複雜度就是在分配元素時，使用的桶空間；所以空間複雜度為：O（10 × length）= O （length）

 

 

 

 

桶排序(Bucket Sort)

 

　　桶排序也叫箱排序。工作的原理是將陣列元素對映到有限數量個桶裡，利用計數排序可以定位桶的邊界，每個桶再各自進行桶內排序（使用其它排序演算法或以遞迴方式繼續使用桶排序）。

桶排序可用於最大最小值相差較大的資料情況，比如[9012,19702,39867,68957,83556,102456]。
但桶排序要求資料的分佈必須均勻，否則可能導致資料都集中到一個桶中。比如[104,150,123,132,20000], 這種資料會導致前4個數都集中到同一個桶中。導致桶排序失效。

桶排序的基本思想是：把陣列 arr 劃分為n個大小相同子區間（桶），每個子區間各自排序，最後合併。
計數排序是桶排序的一種特殊情況，可以把計數排序當成每個桶裡只有一個元素的情況。

1.找出待排序陣列中的最大值max、最小值min
2.我們使用 動態陣列ArrayList 作為桶，桶裡放的元素也用 ArrayList 儲存。桶的數量為(max-min)/arr.length+1
3.遍歷陣列 arr，計算每個元素 arr[i] 放的桶
4.每個桶各自排序
5.遍歷桶陣列，把排序好的元素放進輸出陣列

 

桶排序的邏輯其實特別好理解，它是一種純粹的分而治之的排序方法。

舉個例子簡單說一下大家就知道精髓了。

假如對11,4,2,13,22,24,20 進行排序。

那麼，我們將4和2放在一起，將11,13放在一起，將22,24,20放在一起。  然後將這三部分分別排序（可以根據實現情況任意選擇排序方式，我的程式碼中使用的是快排），將子陣列排序後，再順序輸出就是最終排序結果了（大概應該明白了，我們是根據數字大小進行分組的，故而順序輸出即可）

/*
 * 桶排序
 */
public class BucketSort {
    public static void main(String[] args) {
        int[] arrayData = { 22, 33, 57, 55, 58, 77, 44, 65, 42 };
        BucketSortMethod(arrayData, 10);
        for (int integer : arrayData) {
            System.out.print(integer);
            System.out.print(" ");
        }
    }

    /*
     * buckenCount - 桶的數量
     */
    public static void BucketSortMethod(int[] arrayData, int buckenCount) {
        int[][] arrayBucket = new int[buckenCount][arrayData.length]; // 桶容器

        for (int i = 0; i < arrayBucket.length; i++) {
            for (int j = 0; j < arrayBucket[i].length; j++) {
                arrayBucket[i][j] = -1;
            }
        }

        int[] arrayLength = new int[arrayData.length];
        int num;

        // 將資料分桶
        for (int i = 0; i < arrayData.length; i++) {
            // 根據結果來確定是存在在哪個桶中
            num = arrayData[i] / buckenCount;
            num = 10 - num; // 這是為了降序

            // System.out.println(num);
            arrayBucket[num][arrayLength[num]] = arrayData[i];
            arrayLength[num]++;
        }

        // 將桶內資料進行排序，這裡使用的是快排
        for (int i = 0; i < arrayBucket.length; i++) {
            QuickSort.QuickSortMethod(arrayBucket[i]);
        }

        int resultIndex = 0;
        // 對於桶內的資料進行輸出
        for (int i = 0; i < arrayBucket.length - 1; i++) {
            if (arrayLength[i] > 0) {
                for (int j = 0; j < arrayBucket[i].length; j++) {
                    if (arrayBucket[i][j] != -1) {
                        arrayData[resultIndex++] = arrayBucket[i][j];
                    }
                }
            }
        }
    }
}

 

 

時間複雜度：

時間複雜度主要還是取決於子陣列的排序時間複雜度。 子陣列的排序複雜度平均是O(n*log2n)，然後分桶這塊的的空間複雜度是O(n)

即O(n+n*log2n)

 

空間複雜度：

假設桶的數量是b，待排序陣列的長度是n。

那麼O(b*n)=O(n)

 

穩定性：穩定性主要取決於子陣列中的排序（即44行呼叫的快排），子陣列中使用的排序方法是穩定的，那麼桶排序就是穩定的。

 

.