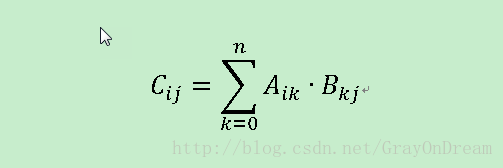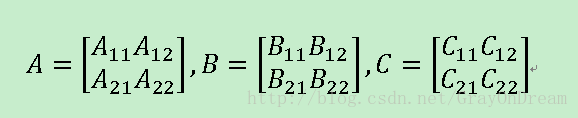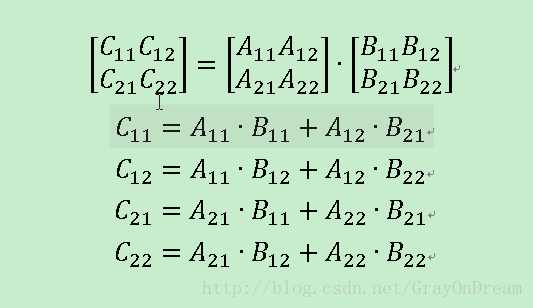矩陣乘積計算（Strassen）

阿新 • • 發佈：2018-12-09

矩陣乘積計算（Strassen）

問題描述

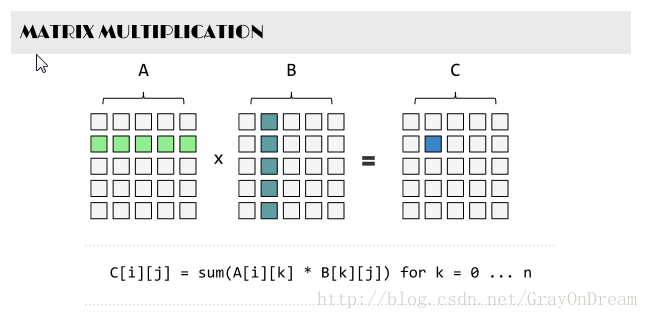
已知A，B兩個矩陣計算其乘積C？

矩陣乘積數學公式：

假設存在兩個矩陣A為m×n矩陣，B為k×l矩陣，若需要計算AB則必須n=k，若需要計算BA必須l=m否則無法進行計算，先假定n=k即B為n×l矩陣則AB的結果為一個m×l的矩陣並且該矩陣每個點的元素的值表示為 $Cij$ 則：

這裡寫圖片描述

方法一：直接計算

直接利用多重for迴圈求出相關矩陣對應的點的值即可

//矩陣的資料結構,隨機矩陣，非特殊矩陣
struct array
{
    int **data;                 //資料域 

    int row;
    int col;
};

/**
 *  初始化矩陣元素，用隨機數填充
 *  只為研究演算法因此為進行相關的記憶體檢查
 *  flag用來標記是否生成空矩陣，即元素全部為0的矩陣
 */
void init_array(struct array *ptr,const int row,const int col,int flag)
{
    int i = 0,j = 0;
    ptr->data = (int **)malloc(sizeof(int)*row);                                    //？？記憶體分配
    for 
 (i = 0; i < row; i++)
    {
        *(ptr->data + i) = (int*)malloc(sizeof(int)*col);                           //？？記憶體分配
    }

    ptr->col = col;
    ptr->row = row;
    srand(time(NULL));
    for (i = 0; i < row; i++)
    {
        for (j = 0; j < col; j++)
        {
            if 
 (flag)
            {
                ptr->data[i][j] = rand() % ARRAY_PRCE;
            }
            else
            {
                ptr->data[i][j] = 0;
            }
        }
    }
}

/**
 *  列印矩陣元素
 */
void print_array(const struct array *ptr, const char *msg)
{
    int i, j;
    printf("%s\n", msg);
    for (i = 0; i < ptr->row; i++)
    {
        for (j = 0; j < ptr->col; j++)
        {
            printf("%4d", ptr->data[i][j]);
        }

        printf("\n");
    }
}
/**
 *  銷燬記憶體
 */
void delete_array(struct array *ptr)
{
    int i = 0;
    for (i = 0; i < ptr->row; i++)
    {
        free(*(ptr->data + i));
        *(ptr->data + i) = NULL;
    }

    free(ptr->data);
}

/*******************************************************************************************

*******************************************************************************************/

/**
*   矩陣乘法求解  
*   問題描述：已知兩個可以進行相乘的矩陣，求的乘積後的結果
*/

/**
*   方法一：暴力直接求解  
*   利用矩陣乘法規則直接進行求解羅列出每個點的值求的最終的矩陣
*/
struct array mult_array(const struct array *ptr1, const struct array *ptr2)
{
    int i = 0;
    int j = 0;
    int k = 0;
    struct array ptr;
    if (ptr1->col != ptr2->row)                         //檢查是否符合可以進行乘積的要求
    {
        return;
    }

    init_array(&ptr, ptr1->row, ptr2->col, 0);
    for (i = 0; i < ptr.row;i ++)
    {
        for (j = 0; j < ptr.col; j++)
        {
            for (k = 0; k < ptr1->col; k++)
            {
                ptr.data[i][j] += ptr1->data[i][k] * ptr2->data[k][j];
            }
        }
    }

    return ptr;
}

執行效果

這裡寫圖片描述

時間複雜度為O( $n^3$ )

方法二：分治演算法

將矩陣分解為一個個小矩陣進行計算然後將計算結果合併得到相關的結果。源於矩陣服從分配率和結合律，並不支援交換律。

三個矩陣本身就可以寫成下面的格式

這裡寫圖片描述

那麼相關的計算可以寫成

這裡寫圖片描述

同理A11等一些子矩陣也可以寫成相關的子矩陣，就這樣將矩陣不斷分解為小矩陣進行計算，最後歸併為一個矩陣。

時間複雜度為O( $n^3$ )

/**
 *  方法二：利用分治思想進行求解
 *  存在問題無法解決不同型別的矩陣的問題，要求矩陣的行列必須為2的n次方，若不符合要求可以使用
 *  補0來構造相關的矩陣
 */
Matrix* Matrix::merge_calc(const Matrix& x)
{
    if (x.row == 1)             //當前的矩陣為單個的元素
    {
        Matrix *ptr = new Matrix(x.row, x.col);
        ptr->clear((this->getElem(0, 0))*(x.getElem(0, 0)));
        return ptr;
    }

    //將第一個矩陣分解為四個子矩陣
    Matrix A11(0,0,row/2,col/2,*this);
    Matrix A12(row / 2, 0, row, col / 2, *this);
    Matrix A21(0, col / 2, row / 2, col, *this);
    Matrix A22(row / 2, col / 2, row, col, *this);
    //將第二個矩陣分解為四個子矩陣
    Matrix B11(0, 0, row / 2, col / 2, x);
    Matrix B12(row / 2, 0, row, col / 2, x);
    Matrix B21(0, col / 2, row / 2, col, x);
    Matrix B22(row / 2, col / 2, row, col, x);

    Matrix *C11 = Matrix::add(A11.merge_calc(B11), A12.merge_calc(B21));
    Matrix *C12 = Matrix::add(A11.merge_calc(B12), A12.merge_calc(B22));
    Matrix *C21 = Matrix::add(A21.merge_calc(B11), A22.merge_calc(B21));
    Matrix *C22 = Matrix::add(A21.merge_calc(B12), A22.merge_calc(B22));

    //將C11，C12，C21，C22合併為一個完整的矩陣
    Matrix* ptr = Matrix::merge(C11, C12, C21, C22);

    return ptr;
}

方法三：Strassen演算法

Strassen演算法同樣是使用分治的思想解決問題，只不過，不同的是當矩陣的階很大時就會採取一個遞推式進行計算相關遞推式為：

                            S1 = B12 - B22
                            S2 = A11 + A12
                            S3 = A21 + A22
                            S4 = B21 - B11
                            S5 = A11 + A22
                            S6 = B11 + B22
                            S7 = A12 - A22
                            S8 = B21 + B22
                            S9 = A11 - A21
                            S10 = B11 + B12

                            P1 = A11 * S1
                            P2 = S2 * B22
                            P3 = S3 * B11
                            P4 = A22 * S4
                            P5 = S5 * S6
                            P6 = S7 * S8
                            P7 = S9 * S10

                            C11 = P5 + P4 - P2 + P6
                            C12 = P1 + P2
                            C21 = P3 + P4
                            C22 = P5 + P1 - P3 - P7

其中A11，A12，A21，A22和B11，B12，B21，B22分別為兩個乘數A和B矩陣的四個子矩陣。C11，C12，C21，C22為最終的結果C矩陣的四個子矩陣。該遞推式是被數學家證明過的。

該演算法的效率為O( $n^(log_27)$ ),但是相對來說額外空間的使用也是很多的。

Matrix* Matrix::strassen_calc(const Matrix& x)
{
    if (x.row < 2)
    {
        return this->force_calc(x);
    }

    //將第一個矩陣分解為四個子矩陣
    Matrix A11(0, 0, row / 2, col / 2, *this);
    Matrix A12(row / 2, 0, row, col / 2, *this);
    Matrix A21(0, col / 2, row / 2, col, *this);
    Matrix A22(row / 2, col / 2, row, col, *this);
    //將第二個矩陣分解為四個子矩陣
    Matrix B11(0, 0, row / 2, col / 2, x);
    Matrix B12(row / 2, 0, row, col / 2, x);
    Matrix B21(0, col / 2, row / 2, col, x);
    Matrix B22(row / 2, col / 2, row, col, x);

    Matrix* S1 = B12 - B22;
    Matrix* S2 = A11 + A12;
    Matrix* S3 = A21 + A22;
    Matrix* S4 = B21 - B11;
    Matrix* S5 = A11 + A22;
    Matrix* S6 = B11 + B22;
    Matrix* S7 = A12 - A22;
    Matrix* S8 = B21 + B22;
    Matrix* S9 = A11 - A21;
    Matrix* S10 = B11 + B12;

    Matrix* P1 = B12 - B22;
    Matrix* P2 = B12 - B22;
    Matrix* P3 = B12 - B22;
    Matrix* P4 = B12 - B22;
    Matrix* P5 = B12 - B22;
    Matrix* P6 = B12 - B22;
    Matrix* P7 = B12 - B22;

    P1 = A11.strassen_calc(*S1);
    P2 = S2->strassen_calc(B22);
    P3 = S3->strassen_calc(B11);
    P4 = A22.strassen_calc(*S4);
    P5 = S5->strassen_calc(*S6);
    P6 = S7->strassen_calc(*S8);
    P7 = S9->strassen_calc(*S10);

    Matrix *C11 = Matrix::sub(Matrix::add(P5, P4), Matrix::sub(P2, P6));
    Matrix *C12 = Matrix::add(P1, P2);
    Matrix *C21 = Matrix::add(P3, P4);
    Matrix *C22 = Matrix::sub(Matrix::add(P5, P1), Matrix::add(P3, P7));

    return Matrix::merge(C11,C12,C21,C22);
}

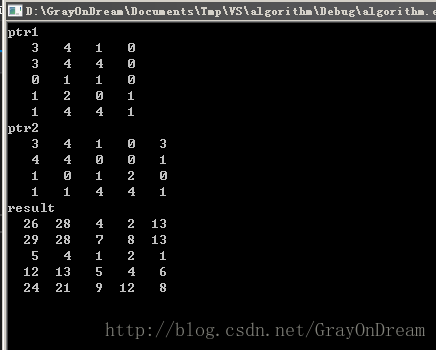
執行效果：

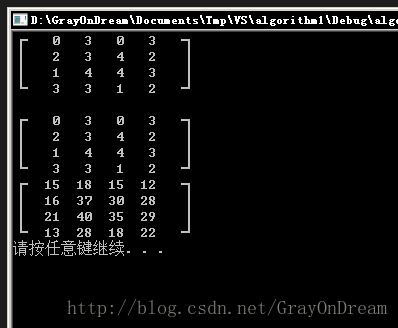
這裡寫圖片描述

完整的程式碼

//Matrix.h
#pragma once
#ifndef _MATRIX_H_
#define _MATRIX_H_

#include <iostream>
#include <vector>
using std::vector;
#define VISE 5
#define GATE 16                 //用來限定使用哪種演算法進行計算

#include <cstdlib>
#include <ctime>

typedef int type;
class Matrix
{
private:
    int row;                            //行
    int col;                            //列
    vector<vector<type>> data;          //資料
public:
    Matrix(int row, int col) :data(row),row(row),col(col)                   //矩陣資料生成利用隨機數進行生成
    {
        for (int i = 0; i < row; i++)
        {
            data[i].resize(col);
        }

        srand(time(0));
        for (int i = 0; i < row; i++)
        {
            for (int j = 0; j < col; j++)
            {
                data[i][j] = rand() % VISE;
            }
        }
    }

    Matrix(int row1, int col1, int row2, int col2, const Matrix& x) :row(row2 - row1), col(col2 - col1),data(row)
    {
        for (int i = 0; i < row; i++)
        {
            data[i].resize(col);
        }

        for (int i = 0; i < row; i++)
        {
            for (int j = 0; j < col; j++)
            {
                data[i][j] = x.getElem(col1 + i, row1 + j);
            }
        }
    }

    Matrix(const Matrix& x)
    {
        *this = x;
    }

    //相關算數運算操作
    Matrix* operator+(const Matrix&);
    Matrix* operator-(const Matrix&);
    Matrix* operator*(const Matrix&);
    static Matrix* add(const Matrix*, const Matrix*);                               //+
    static Matrix* sub(const Matrix*, const Matrix*);                               //-
    static Matrix* merge(const Matrix*, const Matrix*,const Matrix*,const Matrix*); //將四個子矩陣合併為一個矩陣
    //獲取矩陣的相關元素
    vector<type> operator[](const int);             //取得row
    type getElem(const int,const int) const;        //獲取相關節點的資料
    void setElem(const int, const int, type);       //設定節點的資料   

    //計算乘法的演算法
    Matrix* force_calc(const Matrix&);              //直接暴力求解
    Matrix* merge_calc(const Matrix&);              //分治求解
    Matrix* strassen_calc(const Matrix&);           //Strassen演算法

    void show();                                    //列印矩陣
    bool isSimilar(const Matrix& x);                //行列相同即為同類型矩陣
    void clear(type);                               //設定矩陣中所有的元素為同一個指定的值                                

    ~Matrix();
};

#endif
//_MATRIX_H_

//Matrix.cpp
#include "Matrix.h"

Matrix* Matrix::operator*(const Matrix& x)
{
    if (x.row != this->col)
    {
        return nullptr;
    }

    if (x.row < VISE && x.col < VISE && row < VISE && col < VISE)
    {
        return this->merge_calc(x);
    }

    return this->strassen_calc(x);
}

/**
 *  方法一：暴力直接求解問題
 *  時間複雜度為O(n^3)
 */
Matrix* Matrix::force_calc(const Matrix& x)
{
    if (x.row != this->col)                                             //行列不同無法進行乘法，可以進行補零將相關矩陣填充為可使用的矩陣
    {                                                                   //這裡不進行相關的編寫
        return nullptr;
    }

    Matrix *ptr = new Matrix(row, x.col);
    ptr->clear(0);
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < x.col; j++)
        {
            for (int k = 0; k < col; k++)
            {
                ptr->setElem(i, j, ptr->getElem(i, j) + getElem(i, k) * x.getElem(k, j));
            }
        }
    }

    return ptr;
}

void Matrix::clear(type cur = 0)
{
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            data[i][j] = cur;
        }
    }
}

/**
 *  方法二：利用分治思想進行求解
 *  存在問題無法解決不同型別的矩陣的問題，要求矩陣的行列必須為2的n次方，若不符合要求可以使用
 *  補0來構造相關的矩陣
 */
Matrix* Matrix::merge_calc(const Matrix& x)
{
    if (x.row == 1)             //當前的矩陣為單個的元素
    {
        Matrix *ptr = new Matrix(x.row, x.col);
        ptr->clear((this->getElem(0, 0))*(x.getElem(0, 0)));
        return ptr;
    }

    //將第一個矩陣分解為四個子矩陣
    Matrix A11(0,0,row/2,col/2,*this);
    Matrix A12(row / 2, 0, row, col / 2, *this);
    Matrix A21(0, col / 2, row / 2, col, *this);
    Matrix A22(row / 2, col / 2, row, col, *this);
    //將第二個矩陣分解為四個子矩陣
    Matrix B11(0, 0, row / 2, col / 2, x);
    Matrix B12(row / 2, 0, row, col / 2, x);
    Matrix B21(0, col / 2, row / 2, col, x);
    Matrix B22(row / 2, col / 2, row, col, x);

    Matrix *C11 = Matrix::add(A11.merge_calc(B11), A12.merge_calc(B21));
    Matrix *C12 = Matrix::add(A11.merge_calc(B12), A12.merge_calc(B22));
    Matrix *C21 = Matrix::add(A21.merge_calc(B11), A22.merge_calc(B21));
    Matrix *C22 = Matrix::add(A21.merge_calc(B12), A22.merge_calc(B22));

    //將C11，C12，C21，C22合併為一個完整的矩陣
    Matrix* ptr = Matrix::merge(C11, C12, C21, C22);

    return ptr;
}

Matrix* Matrix::strassen_calc(const Matrix& x)
{
    if (x.row < 2)
    {
        return this->force_calc(x);
    }

    //將第一個矩陣分解為四個子矩陣
    Matrix A11(0, 0, row / 2, col / 2, *this);
    Matrix A12(row / 2, 0, row, col / 2, *this);
    Matrix A21(0, col / 2, row / 2, col, *this);
    Matrix A22(row / 2, col / 2, row, col, *this);
    //將第二個矩陣分解為四個子矩陣
    Matrix B11(0, 0, row / 2, col / 2, x);
    Matrix B12(row / 2, 0, row, col / 2, x);
    Matrix B21(0, col / 2, row / 2, col, x);
    Matrix B22(row / 2, col / 2, row, col, x);

    Matrix* S1 = B12 - B22;
    Matrix* S2 = A11 + A12;
    Matrix* S3 = A21 + A22;
    Matrix* S4 = B21 - B11;
    Matrix* S5 = A11 + A22;
    Matrix* S6 = B11 + B22;
    Matrix* S7 = A12 - A22;
    Matrix* S8 = B21 + B22;
    Matrix* S9 = A11 - A21;
    Matrix* S10 = B11 + B12;

    Matrix* P1 = B12 - B22;
    Matrix* P2 = B12 - B22;
    Matrix* P3 = B12 - B22;
    Matrix* P4 = B12 - B22;
    Matrix* P5 = B12 - B22;
    Matrix* P6 = B12 - B22;
    Matrix* P7 = B12 - B22;

    P1 = A11.strassen_calc(*S1);
    P2 = S2->strassen_calc(B22);
    P3 = S3->strassen_calc(B11);
    P4 = A22.strassen_calc(*S4);
    P5 = S5->strassen_calc(*S6);
    P6 = S7->strassen_calc(*S8);
    P7 = S9->strassen_calc(*S10);

    Matrix *C11 = Matrix::sub(Matrix::add(P5, P4), Matrix::sub(P2, P6));
    Matrix *C12 = Matrix::add(P1, P2);
    Matrix *C21 = Matrix::add(P3, P4);
    Matrix *C22 = Matrix::sub(Matrix::add(P5, P1), Matrix::add(P3, P7));

    return Matrix::merge(C11,C12,C21,C22);
}

/**
 *  將四個子矩陣合併為一個完整的矩陣
 *  也可以使用分治思想進行解決，以後可能會新增相關的功能
 */
Matrix* Matrix::merge(const Matrix* p1, const Matrix* p2,const Matrix* p3, const Matrix* p4)
{
    //不符合可以進行合併的條件
    if (!(p1->row == p2->row && p2->col == p4->col && p4->row == p3->row && p1->col == p3->col))
    {
        return nullptr;
    }

    Matrix* ptr = new Matrix(p1->row + p3->row, p2->col + p1->col);
    ptr->clear(0);
    //重新裝值
    for (int i = 0; i < p1->row; i++)
    {
        for (int j = 0; j < p1->col; j++)
        {
            ptr->setElem(i, j, p1->getElem(i, j));
        }
    }

    for (int i = 0; i < p2->row; i++)
    {
        for (int j = 0; j < p2->col; j++)
        {
            ptr->setElem(i, j + p1->col, p2->getElem(i, j));
        }
    }

    for (int i = 0; i < p3->row; i++)
    {
        for (int j = 0; j < p3->col; j++)
        {
            ptr->setElem(i + p1->row, j, p3->getElem(i, j));
        }
    }

    for (int i = 0; i < p4->row; i++)
    {
        for (int j = 0; j < p4->col; j++)
        {
            ptr->setElem(p1->row + i, p1->col + j, p4->getElem(i, j));
        }
    }

    return ptr;
}

Matrix* Matrix::sub(const Matrix* p1, const Matrix* p2)
{
    if (!(p1->col == p2->col && p1->row == p2->row))
    {
        return nullptr;
    }

    Matrix *ptr = new Matrix(p1->row, p1->col);
    for (int i = 0; i < p1->row; i++)
    {
        for (int j = 0; j < p1->col; j++)
        {
            ptr->setElem(i, j, (p1->getElem(i, j) - p2->getElem(i, j)));
        }
    }

    return ptr;
}

Matrix* Matrix::add(const Matrix* p1, const Matrix* p2)
{
    if (!(p1->col == p2->col && p1->row == p2->row))
    {
        return nullptr;
    }

    Matrix *ptr = new Matrix(p1->row, p1->col);
    for (int i = 0; i < p1->row; i++)
    {
        for (int j = 0; j < p1->col; j++)
        {
            ptr->setElem(i, j, (p1->getElem(i, j) + p2->getElem(i, j)));
        }
    }

    return ptr;
}

Matrix* Matrix::operator+(const Matrix& x)
{
    if (!isSimilar(x))
    {
        return nullptr;
    }

    Matrix *ptr = new Matrix(x.row, x.col);                             //記憶體需要釋放
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            ptr->setElem(i, j, this->getElem(i, j) + x.getElem(i, j));
        }
    }

    return ptr;
}

Matrix* Matrix::operator-(const Matrix& x)
{
    if (!isSimilar(x))
    {
        return nullptr;
    }

    Matrix *ptr = new Matrix(x.row, x.col);                             //記憶體需要釋放
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            ptr->setElem(i, j, this->getElem(i, j) - x.getElem(i, j));
        }
    }

    return ptr;
}

vector<type> Matrix::operator[](const int row)
{
    return data[row];
}

type Matrix::getElem(int row, int col)const
{
    return this->data[row][col];
}

void Matrix::setElem(int row, int col, type cur)
{
    this->data[row][col] = cur;
}

void Matrix::show()
{
    for (int i = 0; i < row; i++)
    {
        if (i == 0)
        {
            std::cout << "┏";
        }
        else if (i == row - 1)
        {
            std::cout << "┗";
        }
        else
        {
            std::cout << "┃";
        }

        for (int j = 0; j < col; j++)
        {
            std::cout.width(4);
            std::cout << data[i][j];
        }

        if (i == 0)
        {
            std::cout << "   ┓";
        }
        else if (i == row - 1)
        {
            std::cout << "   ┛";
        }
        else
        {
            std::cout << "   ┃";
        }

        std::cout << std::endl;
    }
}

bool Matrix::isSimilar(const Matrix& x)
{
    return x.row == this->row && this->col == x.col;
}

Matrix::~Matrix()
{
    this->row = 0;
    this->col = 0;
}

矩陣乘積計算（Strassen）

矩陣乘積計算（Strassen）問題描述已知A，B兩個矩陣計算其乘積C？矩陣乘積數學公式：假設存在兩個矩陣A為m×n矩陣，B為k×l矩陣，若需要計算AB則必須n=k，若需要計算BA必須l=m否則無法進行計算，先假定n=k即B為n×l矩陣則AB的結果為一個m

數學-矩陣計算（2）矩陣函式微積分前奏

矩陣微積分會涉及到對矩陣函式操作的規則。例如，假設將一個m×n 的矩陣 X 對映到一個p×q 的矩陣 Y 中。而我們期望獲得的導數表示式如下：對於所有的 i，j 和k，l 來說，這裡主要的困難在於如何將對矩陣內的元素對應的求導，我們在矩陣計算（1）中最後有關矩陣對矩陣的求導

5-5 多邊形周長計算（繼承）

oid int return () equal while per 參數化包含給出下面的多邊形基類框架： class polygon { protected: int number;//邊數，最多不超過100條邊 private: int side_l

Openstack 雲計算（一）： kvm 虛擬機配置

openstack kvm 虛擬化 Openstack 雲計算（一）： kvm 虛擬機配置

天馬行空雲計算（二）-Hardware&Hypervisor介紹

iso 雲計計算 viso alt 視圖 png mage 介紹天馬行空雲計算系列一介紹了總體抽象視圖，本篇展開Hardware&Hypervisor 介紹。如下是介紹大綱：天馬行空雲計算（二）-Hardware&Hypervisor介紹

安全多方計算（MPC）從入門到精通：簡易教程

編程部署門面 html 節點 lin 入門到精通插件之前簡介：JUGO平臺針對企業級用戶，打造基於MPC的安全數據交易平臺。本節內容將介紹具體如何通過在本地部署MPC節點的教程，完成數據協同計算。1.編程語言&開發環境1.1.計算邏輯編程語言　　Frutt

安全多方計算（MPC）從入門到精通：JUGO－IDE及SDK

限制異常側邊欄錯誤信息工作目錄 exp png 文件內容則表達式簡介：在上一節《安全多方計算（MPC）從入門到精通：Frutta語言》中，已經介紹了Frutta語言語法相關的內容，在本節中，我們將介紹JUGO－IDE及SDK。1.什麽是JUGO-IDE　　JUG

安全多方計算（MPC）從入門到精通：經典案例

err .html 希望 org 安裝nginx 錯誤碼 rri dst 14. 簡介：在上一節《安全多方計算（MPC）從入門到精通：JUGO－IDE及SDK》中，已經介紹了JUGO－IDE及SDK相關的內容，本節也是本系列的最後一篇文章，我們將介紹MPC的經典案例，以及這

矩陣求導（下）——矩陣對矩陣的求導

參考：https://zhuanlan.zhihu.com/p/24863977 本篇使用小寫字母x表示標量，粗體小寫字母 x \boldsym

矩陣求導（上）——標量對矩陣的求導

參考：https://zhuanlan.zhihu.com/p/24709748 這部分內容分兩篇整理，上篇講標量對矩陣的求導，下篇講矩陣對矩陣的求導。本文使用小寫字母x表示標量，粗體小寫字母

矩陣快速冪（hdu1575）

矩陣快速冪和一般的整數快速冪是非常相似的首先會以下一般的快速冪 int pow(int n,int k) { int ans=1; while(k) { if(k&1) ans*=n; k>>

矩陣快速冪（模板）

#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int maxn = 2; const int mod = 10000; //矩陣結構體 stru

劍指Offer 51. 構建乘積陣列（陣列）

題目描述給定一個數組A[0,1,...,n-1],請構建一個數組B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。題目地址 https://www.nowcoder.com/practice/94a4d381a

LeetCode-中級-矩陣置零（JavaScript）

給定一個 m x n 的矩陣，如果一個元素為 0，則將其所在行和列的所有元素都設為 0。請使用原地演算法。示例 1: 輸入: [ [1,1,1], [1,0,1], [1,1,1] ] 輸出: [

邊緣計算（1）

邊緣計算：萬物互聯時代新型計算模型施巍鬆主要解決 1.海量的邊緣資料的集中處理 2.邊緣資料傳遞到中心使用的頻寬負載 3.網路邊緣的個人隱私問題 4.傳輸過程中使用電能很大邊緣計算能做的：將雲資料中心的一些計算任務進行分解，遷移到邊緣節點進行處理，進而降低資料中心的負

C#賦值並進行簡單計算（dotnetcore）

使用vscode在dotnetcore環境下開發,C#賦值並進行簡單計算建立dotnetcore專案：不會的參考：使用vs code 建立.net core控制檯應用程式 : https://blog.csdn.net/qq_36051316/article/details/84

可達使用者投資額的計算（Java）

有話要說：前陣子遇到了一個計算可達使用者投資額的問題，覺得非常有趣，故把它記錄下來。問題描述：某產品可被投資，註冊後才可以投資，其註冊可以被邀請（並不是每個人都是被邀請的）。邀請人可以邀請多個人註冊投資，而被邀請人只能有一位邀請人。也就是說邀請人與被邀請人是一對多的關係。現給定兩組資料：邀請與被邀請的

服務計算（2）：go環境配置與學習

Go語言學習環境配置使用yum install 使用命令sudo yum install -y golang 直接下載安裝包環境：騰訊雲主機 Ubuntu 16.04 具體見官方文件。首先下載安裝包：wget https://studygolang.c

矩陣快速冪（模版）快速乘 + 快速冪 + 矩陣快速冪

矩陣快速冪：首先前置技能: 快速冪 + 矩陣乘法。 1 快速冪 1.1 快速乘法 1.1.1 引用自2009年國家集訓隊論文，駱可強：《論程式底層優化的一些方法與技巧》（膜膜膜）可以根據需要換成uLL (unsigned long long)

移動計算（三）

即前面兩節講的安卓開發的基本過程後我們來講一下移動計算方面的，個人認為移動計算，手機等裝置不只是進行訊息傳遞及獲取資訊的工具而是具有一定的計算能力.這裡我們主要介紹在手機端進行影象處理，利用的是OPENCV庫。首先我們來試一下opencv for Androi

矩陣乘積計算（Strassen）

矩陣乘積計算（Strassen）

問題描述

矩陣乘積數學公式：

方法一：直接計算

執行效果

方法二：分治演算法

方法三：Strassen演算法

完整的程式碼

相關推薦