問題描述：給定平面上N個點的座標，找出距離最近的兩個點。

這是程式設計之美2.11的一道題目，從昨天到現在就一直在設法解決它；如果用常規的解法，只需要將N個點兩兩計算距離，然後找出最小距離的兩個點就可以了；但是這種解法的演算法複雜度為O(N^2); 為了降低演算法的複雜度，我們需要有更好的方法。這裡我們找到的解法是分治法。

設點集為S，|S|=N，S的橫座標集合為Sx，縱座標集合為Sy;

演算法的步驟如下：

1.找出Sx的中位數:median_Sx;用median_Sx對點集S進行劃分，左邊的為S1，右邊的為S2;

2.分別求出S1和S2中的最近點對，設S1和S2中最近點對的距離分別為:delta(S1), delta(S2);

3.求出S1和S2最近點對距離的較小值：Delta = min{delta(S1), delta(S2)};

4.找出S2中y值前6大的點，設為S2’.(此處不用排序，用O(n)時間找出第i大的點，因為排序的時間複雜度為O(n*logn), 網上絕大部分的演算法是用排序，顯然用排序的方法來找出前6大的點效率低下）;

5.對於S1中的每一個點，與S2’中的每一個點計算距離delta’, 如果delta’ < Delta，令Delta=delta’;

現在我們分析一下上述演算法的時間複雜度，由於我們採用中位數進行劃分，每一次劃分都能確保點集被分為大小相當的兩個部分，所以：

T(n)= 2*T(n/2) + 合併複雜度。 由於合併的時候，是用S1中的n/2個點和S2中最多6個點進行比較，比較的次數為n/2 * 6 = 3n. 所以

T(n)= 2*T(n/2)+O(n). 由《演算法導論》中文第二版44頁的主定理，可知T(n) = O(n*log(n));

演算法第4步中，為什麼只用選取S2中最多前6大的6個點進行比較呢？對這個問題，《程式設計之美》上沒有說清楚，這裡再詳細的論證下；

如下圖所示：

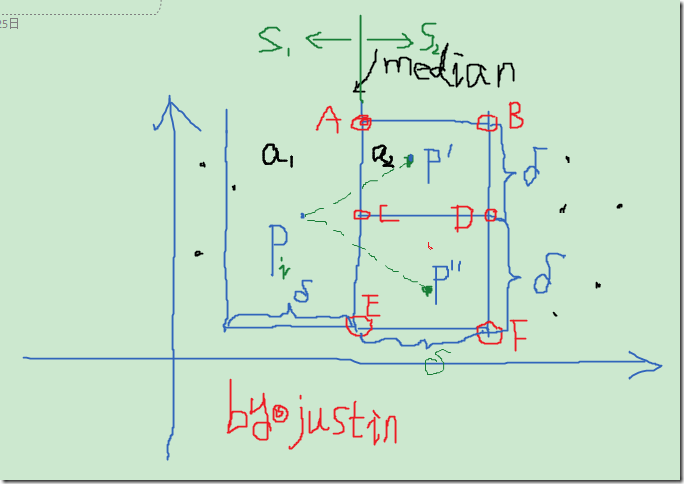
在上圖中，我們有一系列的點，按照上述的演算法，我們利用median(中位數)將點分為了S1和S2兩個部分，安裝演算法的第2、3步我們可以求得δ，在圖中median線的左邊和右邊，距離其δ的距離，分別作兩條直線，和直線median一起，我們得到了兩個區域，分別為a1、a2，如圖所示。由於δ是S1和S2中距離較小者，由此可知，a1和a2區域內不可能再存在距離<δ

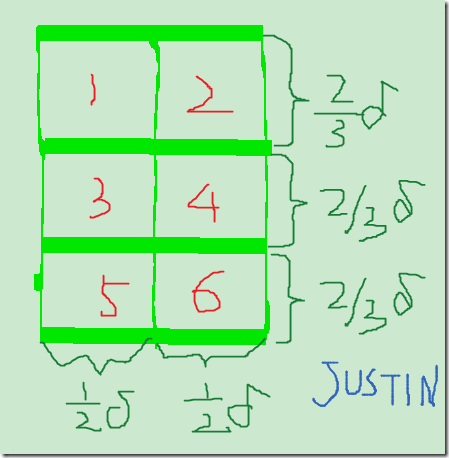
根據δ定義，我們知道，a2中的任意兩點的距離都必須大於δ，否則與δ的定義相矛盾。如下圖所示，我們將δ*2δ的矩形區域，分成邊長為1/2δ *2/3δ的六個小矩形，如圖中的紅色編號1..6所示。我們假設該區域內的點大於6個，那麼根據鴿籠原理，那麼必然有一個小矩形中存在至少兩個點，這兩個點的距離必然小於邊長為1/2δ *2/3δ矩形的對角線，即D^2<（1/2δ)^2 + (2/3δ)^2=(5/6δ)^2<δ^2;所以a2矩形區域當中的點數不可能大於6.最多就6個點，這種情況是如上圖中紅色的A,B…EF所示。

本問題的程式碼如下所示（有點長），有錯誤的地方還望大家批評指正~~

/*
Author:JustinZhang
Time:2012年4月24日11:29:25
End: 2012年4月25日16:56:35
Email:[email protected]
Desc:平面上有N個點，找出N個點中距離最近的兩個點；如果用窮舉法，那麼演算法的複雜度將達到O(n^2)；
本演算法採用分治法，可以將複雜度降低到O(n*log(n));
*/
 
 
#include <iostream>
#include <vector>
#include <iomanip>
#include <algorithm>
#include <cmath>
using namespace std;
 
//delta=min{min(dest(S1), min(dest(S2}}.
double delta = INT_MAX;
 
void swap(int &x, int &y)
{
    int tmp = x;
    x = y;
    y = tmp;
}
//插入排序演算法
void insert_sort(vector<int>&A, int p, int r)
{
    int i,j;
    int key = 0;
    for (i=p+1; i<=r; i++)
    {
        key = A[i];
        j = i - 1;
        while (j>=p && A[j]>key)
        {
            A[j+1] = A[j];//將A[j]往前移動
            j--;
        }
        A[j+1] = key;
    }
}
 
//將整型容器劃分為兩個部分
int partion(vector<int> &A,int p, int r)
{
    int count = p - 1;
    int key = A[r];
 
    for (int i=p; i<=r-1; i++)
    {
        if (A[i] < key)
        {
            count++;
            swap(A[count],A[i]);
        }
    }
    swap(A[count+1],A[r]);
    return count+1;
}
 
//根據演算法導論上的思想，取得中位數的中位數
int get_median(vector<int>&data, int p, int r)
{
    int i=0, j=0;
    int n = r - p + 1;            //獲得原始陣列資料個數
    int remains = n%5;
    int int_count = n - remains;
    int int_group = int_count/5;
    int group_count = (n+4)/5;   //計算出五個元素一組的組數；
 
    //int *group_median = new int[group_count];
    vector<int> group_median(group_count);
 
    if (p==r)
    {
        return data[p];
    }
    //以下程式碼求出五個元素為一組的中位數
    if (0 == remains) //如果元素的個數正好可以分為以5個元素為單位的整陣列
    {
        for (i=p; i<=r-4; i=i+5)
        {
            insert_sort(data, i, i+4);
            group_median[(i-p)/5] = data[p+2];
        }
    }
    else
    {
        for (i=p; i<=(r-remains-4);i=i+5)
        {
            insert_sort(data, i, i+4);
            group_median[(i-p)/5] = data[i+2];
        }
        //處理不夠5個元素的組，改組開始的序號為r-remains+1，結束序號為r
        insert_sort(data,r-remains+1,r);
        group_median[group_count-1] = data[r-remains+1+remains/2];
    }
    if (group_count==1)
    {
        return group_median[0];
    }
    else
    {
        return get_median(group_median,0,group_count-1);
    }
    return 0;
}
 
/*就是因為get_position函式寫錯了，導致很久都沒有能夠發現錯誤，要仔細啊~~*/
int get_position(vector<int> &A, int p, int r, int key)
{
    for (int i=p; i<=r; i++)
    {
        if (A[i]==key)
        {
            return i;
        }
    }
 
    return -1;
}
 
//該函式是為了找到陣列A中，第seq小的數
int select(vector<int> &A,int p, int r, int seq)
{
    //獲得陣列A的中位數的中位數，將其作為劃分陣列的支點
    int pivot_key = get_median(A, p, r);
    int pos = get_position(A,p,r,pivot_key);
    swap(A[pos],A[r]);
    int i = partion(A, p, r);
    int x = i - p + 1;
    if (seq == x)
    {
        return A[i];
    }
    else if (seq < x)
    {
        select(A, p, i-1, seq);
    }
    else
    {
        select(A, i+1, r, seq-x);
    }
 
}
 
 
 
class Point
{
public:
    int x;
    int y;
    Point(int x=0, int y=0)
    {
        this->x = x;
        this->y = y;
    }
    Point& operator=(const Point &p)
    {
        this->x = p.x;
        this->y = p.y;
        return *this;
    }
    Point(const Point &pp)
    {
        this->x = pp.x;
        this->y = pp.y;
    }
    friend ostream &operator<<(ostream &os, const Point & p)
    {
        os<<"("<<p.x<<"," << p.y << ")";
        
        return os;
    }
 
};
//將兩個點交換
void swap_point(Point &p1, Point &p2)
{
    Point tmp = p1;
    p1 = p2;
    p2 = tmp;
}
//根據點容器的最後一個點，將點集合劃分為兩個部分
int partion_Point_Set(vector<Point> &p,int l, int r)
{
    int count = -1;
    int key = p[r].x;
    for (unsigned i=0; i<=p.size()-2; i++)
    {
        if (p[i].x<key)
        {
            count++;
            swap_point(p[i],p[count]);
        }
    }
    swap_point(p[count+1],p[r]);
    return count+1;
}
//獲得兩點間的距離
double Distance(const Point &p1, const Point &p2)
{
    int x = (p1.x - p2.x);
    int y= (p1.y - p2.y);
    double distance = sqrt((double)(x*x+y*y));
    return distance;
}
//找到兩個數的最小值
double min(double x, double y)
{
    if (x>y)
    {
        return y;
    }
    else
    {
        return x;
    }
        
}
//按照點的x座標來檢索點在容器中的位置
int get_point_position_x(const vector<Point> &p, int l, int r, int x_key)
{
    for (int i=l; i<=r; i++)
    {
        if (p[i].x == x_key)
        {
            return i;
        }
    }
    return -1;
}
//按照點的y座標來檢索點在容器中的位置
int get_point_position_y(const vector<Point> &p, int l, int r, int y_key)
{
    for (int i=l; i<=r; i++)
    {
        if (p[i].y == y_key)
        {
            return i;
        }
    }
    return -1;
}
 
 
//找到p中y座標第order大的點
Point select_point(vector<Point> &p,int l, int r, int order)
{
    vector<int> point_y; 
    for (int i=l; i<=r; i++)
    {
        point_y.push_back(p[i].y);
    }
    int key_y = select(point_y,0,point_y.size()-1,order);
    int position_y = get_point_position_y(p, 0, p.size()-1,key_y);
    return p[position_y];
}
 
double get_minimum_distance(vector<Point> &p,int l, int r,vector<Point> &result)
{
 
    int i=0,j=0;
 
   if ((r-l+1)==2)//如果點數為兩個
    {
        double ret = Distance(p[l],p[r]);
 
        if (ret < delta)
        {        
        result[0]=p[l];
        result[1]=p[r];
        }
 
 
        return ret;
    }
    else if ((r-l+1)==3) //如果點數為3個
    {
        double tmp_dis1 = Distance(p[l],p[l+1]);
        double tmp_dis2 = Distance(p[l],p[l+2]);
        double tmp_dis3 = Distance(p[l+1],p[l+2]);
        double ret = min(min(tmp_dis1,tmp_dis2),tmp_dis3);
 
    if (ret <delta )
    {
        
        if (tmp_dis1 == ret)
        {
            result[0] = p[l];
            result[1] = p[l+1];
        }
        else if (tmp_dis2==ret)
        {
            result[0]=p[l];
            result[1]=p[l+2];
        }
        else
        {
            result[0]= p[l+1];
            result[1]= p[l+2];
        }
    }
        return ret;
    }
    else //大於三個點的情況
    {
        //求出點集p的x座標和y座標
        vector<int> Pointx;
        vector<int> Pointy;
        for (i=l; i<=r; i++)
        {
            Pointx.push_back(p[i].x);
            Pointy.push_back(p[i].y);
        }
        //找到點x座標的中位數
        int x_median = select(Pointx,0,Pointx.size()-1,(Pointx.size()+1)/2);
        int point_median_pos = get_point_position_x(p,l,r,x_median);
        swap_point(p[point_median_pos],p[r]);
        //利用找到的中位數對點集進行劃分
        int point_pivot_index = partion_Point_Set(p,l,r);
        //利用x座標作為中位數，將點集合劃分好後，遞迴的求中位數左邊點集S1和右邊點集合S2距離最小值；
        //考慮如何將距離最小的兩個點儲存下來
        double min_s1 = get_minimum_distance(p,l,point_pivot_index,result);
        double min_s2 = get_minimum_distance(p,point_pivot_index+1,r,result);
        if (min_s1>min_s2)
        {
            delta = min_s2;
        }
        else
        {
            //result[0] = tmp_result1;
            //result[1] = tmp_result2;
            delta = min_s1;
        }
        //現在已經遞迴的求到了S1和S2中點集合最短距離，下面開始求S1和S2之間點之間的距離
        //找出點集合S2中，y座標前六大的點,如果|S2|<6，則只需找出|S2|個點
        int size_s2 = (r-point_pivot_index<6)?r-point_pivot_index:6;
        vector<Point> S2;
        Point tmp;
        for (i=1;i<=size_s2;i++)
        {
            tmp = select_point(p,point_pivot_index+1,r,i);
            S2.push_back(tmp);
        }
 
        for (i=l; i<=point_pivot_index; i++)
        {
            for (j=0; j<size_s2; j++)
            {
                double d = Distance(p[i],S2[j]);
                if (d < delta)
                {
                    result[0]= p[i];
                    result[1]= S2[j];
                    delta = d;
                }
            }
        }
                
        return delta;
    }
}
 
void getinput(vector<Point> &p)
{
    int i;
    Point pp;
    int Pointnumber = 0;
    cout << "please input Point numbers" <<endl;
    cin >> Pointnumber;
    for (i=0; i<Pointnumber; i++)
    {
        cin >> pp.x;
        cin >> pp.y;
        p.push_back(pp);
    }
 
}
 
 
int main()
{
 
    vector<Point> result(2);
    vector<Point> input;
    getinput(input);
    
    double minimum_distance = get_minimum_distance(input,0,input.size()-1,result);
    cout << "The nearest point is: "<<result[0] << " and " << result[1] << endl;
    cout << "their distance is : "<<minimum_distance << endl;
 
    return 0;
}