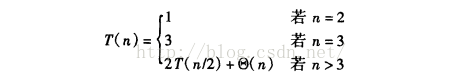設S是平面上n個點的集合，在S中找到兩點p、q，使得他們的歐幾里得距離d(p,q)是所有點對中最小的。

樸素的演算法是計算所有點對的距離，在求出最小的，需要Ω(n²)。

採用分治法可以在Θ(nlogn)完成任務。

基本思路：

我們用分治正規化來解釋這一過程：

（a）劃分階段：

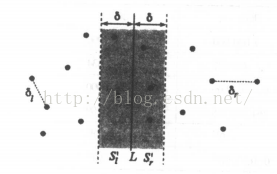
用一條垂直線L把S劃分成兩個儘可能大小接近的子集S_l、S_r，S_l包含左邊的n/2各點，S_r包含右邊的(n+1)/2個點。分別計算出S_l、S_r中的最近點對距離δ_l、δ_r。再計算S_l的點與S_r的點之間的最小距離δ’。

（b）治理階段：

這一階段需要計算出δ’，如果樸素的計算所有S_l中的點到S_r中所有點的距離，需要Ω(n²

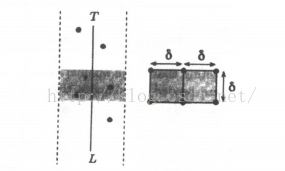
設δ=min{δ_l，δ_r}，可以理解，我們要找的點不會再L兩邊δ距離以外的範圍，只會在下圖中的灰色部分，我們把這一部分稱為T。

我們有下面這麼一個結論：

T中的每個點最多需要和T中的7個點進行比較。(*)

下面解釋一下這個結論的由來：

我們劃分出δ*2δ的矩形，如果該矩形內任意兩點之間的距離不超過δ，這個矩形最多能容納8個點，其中至多4個點屬於S_l，至多4個點屬於S_r。但有兩個點分別在矩形上下邊的中點時，可以取得最大點數。因此最多隻需要比較7次。

現在考慮演算法中怎麼得知我們需要比較哪7個點呢？

實際操作就是不要考慮，我們儘可以多比較幾次，常數的增長並不會帶來太大的影響。所以我們可以將T

（c）組合階段：

很明顯，最近點對距離：δ=min{δ_l，δ_r，δ’}。

演算法分析:

治理階段需要排序，但我們可以先對點按x、y軸座標進行一次排序並存儲，在治理階段只做提取的操作Θ(n)，排序結果依然存在，所以我們的遞推式是：

經過計算：

演算法的複雜度為Θ(nlogn)。

虛擬碼：

*實際上只需要4個點，詳見周玉林、熊鵬榮、朱洪，《求平面點集最近點對的一個改進演算法》。