分別求解損失函式L(w,b)對w和b的偏導數，對於w，當偏導數絕對值較大時，w取值移動較大，反之較小，通過不斷迭代，在偏導數絕對值接近於0時，移動值也趨近於0，相應的最小值被找到。

η選取一個常數引數，前面的負號表示偏導數為負數時（即梯度下降時），w向增大的地方移動。

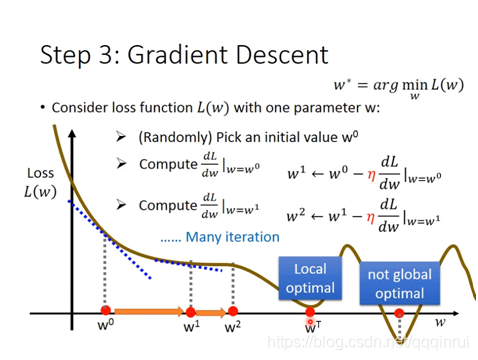
對於非單調函式，可能會陷入區域性最優的情況，可以通過設定不同的w初始值，來對比不同引數下的損失函式值。梯度下降法未必是最優的計算權重引數的方法，但是作為一種簡單快速的方法，經常被使用。

過擬合（overfitting）：

模型過於複雜（所需要的引數較多），而樣本數較少時就會出現過擬合的現象，表現為模型在

學習率（Learning Rate）：

前面梯度下降中的η就是學習率，學習率的大小決定了網路找到最優解需要迭代的次數，學習率越大，需要迭代的次數越少，但是可能越過最優值；學習率越小，優化效率較低，長時間可能無法收斂。

針對不同的資料量、損失函式等一些具體情況，學習率需要做相應的調整，有如下幾種方式：

1、η/N，表示隨著樣本數量的增加，需要的學習率越小，因為偏導數會隨著訓練資料的增多而變大（樣本越多，損失函式越大），因此學習率相應的設定更小的值

2、選擇一個不被訓練集樣本個數影響的成本函式，如均方平均值

3、在每次迭代中調節不同的學習率

基本思路：離最優值越遠，需要朝最優值移動的就越多

解決方法：每次迭代後，使用估計的模型引數檢查誤差函式值，如果相對一上一次迭代，錯誤率減少了，就可以增大學習率；如果增大了，就重新設定上一輪的w值，並減少學習率到之前的一半。

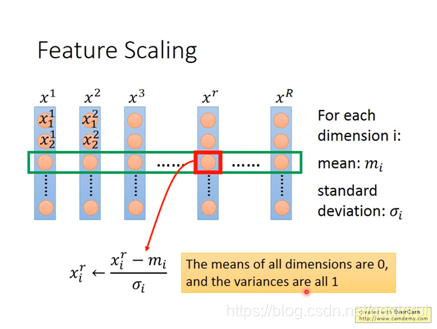
4、歸一化輸入向量：mix-max

分析梯度大小：

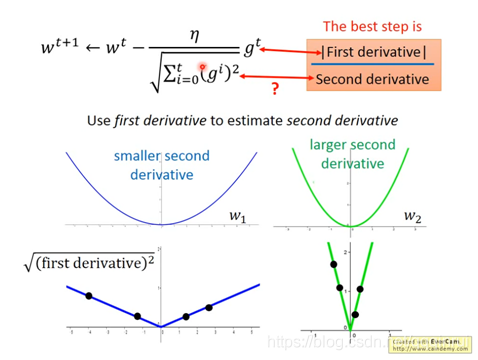
由前面可知，梯度大小 = 學習率*一次偏導，反映了偏導數絕對值越大，w取值離最小L函式越遠，梯度可設定越大；但並非完全如此，偏導數變化的快慢也影響了其與最優解的距離，即同樣的偏導數值，偏導數變化越快，說明離最優解越近，因此，梯度大小還與偏導數的變化率有關係，即二次偏導，二次偏導越大，距離越小。此時，學習率 =η/二次偏導。Adagrad給出一個近似的二次偏導式子，可減少計算量

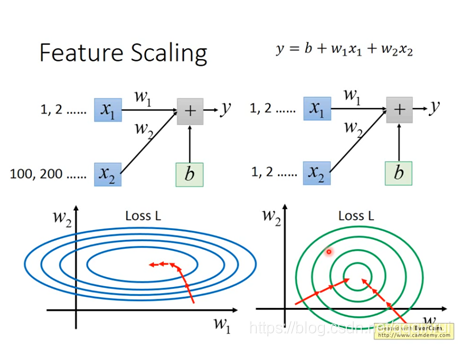
Feature Scaling：

梯度下降的過程中，由於w1和w2對loss函式的影響程度不同，表現為橢圓形，梯度下降的過程中不是朝著圓心走，效率會低一些，通過Feature Scaling，使得各權重佔比一致，梯度朝著圓心走。