理解：機器學習各種演算法的求解最終出來的幾乎都是求解最優模型引數的優化問題。

前言

       在優化問題領域有些很多優秀思想和演算法，從約束條件分類 分為無約束條件的優化和有約束條件的優化問題，有約束條件優化分支裡面又分為了等式約束條件和不等式約束條件，想不想逐一瞭解一下，本篇部落格讓我們一起來看一下無約束條件的演算法之一，叫做梯度下降 (GD)。

數學概念-梯度

       求導是高中數學上層中的內容，想必大家都有所耳聞，沒有把所有數學還給老師，其實對於數學不好的同學可以自己買兩本書回顧一下，我們沒有學好數學也不能怪咱們學的不好，只能說是那個老師沒有教好，學的時候是為了應付考試不知道數學的重要性，自從幹上機器學習感覺數學的價值發揮出來了，每一個概念和公式都是那麼熠熠生輝、流光溢彩，覺的是前人發明這個概念是順其自然 同時也讚歎前輩們智慧超能的大腦，竟然發明出來了這麼多概念，以後又非常重要。
       現在我們求y=x^2的導數，大家一看 為f’(x)=2x ,計算非常快，不過對於數學概念最大的誤區就是不能死記公式，一定要理解求導以及導數的定義以及意義，如此在數學領域才能一步步走的更遠。

定義：
導數（Derivative）是微積分中的重要基礎概念。當函式y=f(x)的自變數x在一點x0上產生一個增量Δx時，函式輸出值的增量Δy與自變數增量Δx的比值在Δx趨於0時的極限a如果存在，a即為在x0處的導數，記作f’(x0)或df(x0)/dx。

       從定義可以看出來導數表示的是因變數增量Δy和自變數增量Δx的比值，也就是自變數變化一點點時因變數變化了多少，表示因變數隨自變數變化的快慢程度，正規一點表示就是一個函式在某一點的導數描述了這個函式在這一點附近的變化率。如果函式的自變數和取值都是實數的話，函式在某一點的導數就是該函式所代表的曲線在這一點上的切線斜率。導數的本質是通過極限的概念對函式進行區域性（某點）的線性逼近。
       生活中複雜的事物比簡單的事物多，如果自變數變為2維、3維甚至更多時，這個導數如何求得，令其它自變數為常數，分別對各個維度單獨求導數即偏導數，對某個點的變化率引入新的概念叫做梯度，可以理解梯度是導數的昇華和抽象，是為了在多維空間描述多維空間函式變化快慢程度的量，它是一個向量，沿著梯度的方向移動是函式變化最快的方向，先看下定義：

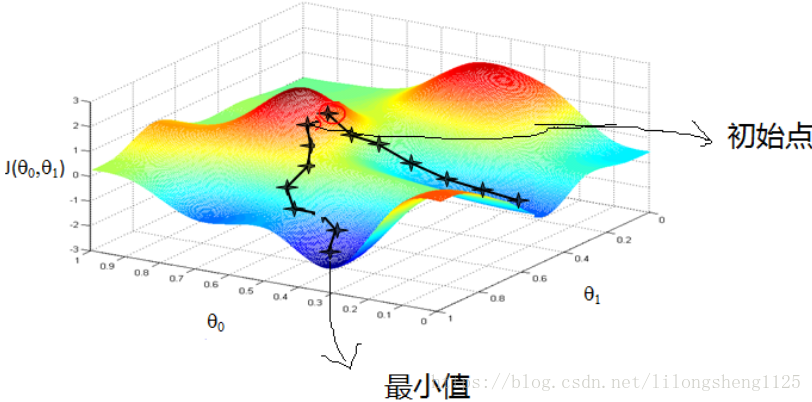
來看一下梯度的直觀解釋，如下圖：

       假設三維空間函式的幾何空間圖形如上所示，我們現在要找到全域性最小值，該怎麼樣求解呢？大家最常想到的是求導 令導數為零，這是一種方法，只是如果導數不能夠求出來時就不太管用了，我們可以用梯度下降法來求解，梯度即高維空間的導數可以看成是函式圖形坡度變化的速率，理論上無論沿著哪個方向都可以找到最小值，無非在圖形上多轉幾圈，需要持續大量計算，如果想盡可能快的找到最優的下坡路線圖，那麼需要藉助於梯度大小來確定，每次都朝著梯度最大值方向移動可見是最陡的路走，下坡將會非常快。

       從圖中還可以看到出現了兩條路徑，此問題也很好理解，設想你在一座山上，下山的路眾多，你可能從山頂一下能看到最優的下山路線，但是計算機並不知道它沒有眼睛，我們告訴它的規則是哪裡陡峭就走哪裡的思路，你覺得它一定能安全的山下嗎？如果最陡峭的地方連著另一個山就走不出去了，到了一個區域性最小點那裡，因此單純的梯度下降是很難找到全域性最優值得。

       在解決這類極值問題的時候，我們往往想讓函式為凸函式，這樣梯度演算法找出來的結果就是全域性最優值，在解決實際問題時 我麼的損失函式是否為凸函式呢？這就需要知道啥叫凸函式，在數學上有定義和定理，如果一個函式的海森矩陣是正定的它就是凸函式，還有啥半正定、行列式、主子式等等，涉及的數學知識較多，發現很多的實際問題模型，背後都離不開數學理論的支援，可以說數學是一門凝縮精華的學科，掌握了數學即可掌握世界的發展。

機器學習中梯度

       在機器學習中，哪裡可以用到梯度求解演算法呢，其實哪裡都可以用到只要求解最優值問題都可以將梯度方法用上，不過最常用的地方還是是求解損失函式的最小值，通過損失函式最小值求出來模型引數，損失函式一般代表著設計模型和真實值之間誤差多少的代表，從理論上來說 不考慮結構化風險 這個誤差當然是越小越好，這就引出了梯度求解損失函式最優值問題，每個模型原理和複雜度不一樣表示式也不一樣，本質是一樣的最優值問題。

應用實戰

       在機器學習實戰一書中，邏輯迴歸裡面再求最小誤差公式時，利用梯度上升演算法來求解，本質和梯度下降是一樣的東西，有多少個樣本就對模型引數訓練了多少次，主要程式碼如下：

def stocGradAscent0(dataMatrix,classLabels):
    '''
        獲取最佳擬合引數向量
    :param dataMatrix:資料集
    :param classLabels:類別標籤
    :return:最佳擬合引數向量
    '''
    m,n = np.shape(dataMatrix)
    print "m = %s,n = %s " % (m,n)
    # 步長
    alpha = 0.01
    # 初始化擬合引數向量
    weights = np.ones(n)
    print "weights %s = " % weights
    # 對迴歸係數進行樣本數量的梯度上升，每次僅僅使用一個樣本
    for i in range(m):
        print "dataMatrix[i] = %s" % dataMatrix[i]
        # h為單一樣本的預測結果
        h = sigmoid(sum(dataMatrix[i] * weights))
        # error為單一樣本的誤差
        error = classLabels[i] - h
        # 根據單一樣本結果來更新迴歸係數
        weights = weights +alpha * error * dataMatrix[i]
    return weights

在求解的時候通常利用矩陣進行計算，簡介明瞭，矩陣包含的資訊多看起來就簡單，簡單唯美。

優化

       步長(learning rate):即每次走的時候朝著梯度方向走多遠，梯度是一個向量，給我們確定走路的方向和大小，但是需要走向量的多少需要我們自己來確定，這個是一個可以持續優化的引數，步長選取是否合理對求解結果也會有影響。

       損失函式(loss function):為了評估模型擬合的好壞，通常用損失函式來度量擬合的程度。損失函式極小化，意味著擬合程度最好，對應的模型引數即為最優引數。
線上性迴歸中，損失函式通常為樣本輸出和假設函式的差取平方。比如對於m個樣本（xi,yi）(i=1,2,…m),採用線性迴歸，損失函式為：

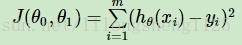
　　　　其中xi表示第i個樣本特徵，yi表示第i個樣本對應的輸出，hθ(xi)為假設函式。
根據訓練模型時樣本個數分類如下：
- 批量梯度下降（Batch Gradient Descent)
言簡意賅批量的意思是樣本一批一批傳給模型，讓模型從中訓練模型引數，如果有10萬樣本一次給模型5萬，兩次即可完成訓練過程，即求解兩次梯度如此求出來的結果很可能不太準確
- 隨機梯度下降 (Stochastic Gradient Descent)
隨機梯度下降是每次採用一個樣本來進行訓練模型，假如10萬個樣本點那麼得訓練10萬次，次數變多了像目標收斂的速度自然就變短了，訓練速度加快，因為模型一般是利用矩陣來進行計算，隨著樣本增多矩陣會越來越大，矩陣非常大時速度就會變慢。
小批量梯度下降 (Min Batch Gradient Descent)
此種方法介於批量和隨機梯度之間，樣本個數分成了很多小份來不斷更新模型，好像這種模式更常用一些，類似於交叉驗證，這也讓我聯想到這中庸之道旨在於一箇中和問題，在生活中同樣是這種道理凡是不能走極端，採取雙方都收益實現雙贏的局面才是最好的。

疑問

梯度法與最小二乘法區別 ？

最小二乘法（又稱最小平方法）是一種數學優化技術。它通過最小化誤差的平方和尋找資料的最佳函式匹配。利用最小二乘法可以簡便地求得未知的資料，並使得這些求得的資料與實際資料之間誤差的平方和為最小。

在我們得到我們的損失函式時正好也是利用了這一點，誤差平方和最小原理，出來了我們的損失函式，
梯度法是迭代法的一種，可以解決各種最優化問題（包括最小二乘問題），也可以翻過來理解，即如果把最小二乘看做是優化問題的話，那麼梯度下降是求解方法的一種。
最小二乘還有狹義和廣義之分，
線性迴歸的模型假設，這是最小二乘方法的優越性前提，否則不能推出最小二乘是最佳（即方差最小）的無偏估計，具體請參考高斯-馬爾科夫定理。特別地，當隨機噪聲服從正態分佈時，最小二乘與最大似然等價。

關於計算
計算一個矩陣的逆是相當耗費時間的, 而且求逆也會存在數值不穩定的情況 因而這樣的計算方法有時不值得提倡.相比之下, 梯度下降法雖然有一些弊端, 迭代的次數可能也比較高, 但是相對來說計算量並不是特別大. 而且, 在最小二乘法這個問題上, 收斂性有保證. 故在大資料量的時候, 反而是梯度下降法 (其實應該是其他一些更好的迭代方法) 更加值得被使用.。

總結

       梯度下降演算法是眾多優化演算法中的一個，他的原理是順著梯度方向逐步迭代求解，一步一步像最優解靠近最終得到最優解的過程，在演算法解法中如動態規劃、貪心演算法其實好多地方用到了迭代的方式解題，這種方式效率高，比普通的迴圈要高一些，在函數語言程式設計中大部分利用這種思想來編寫程式，還是老套路在學習一個演算法的時候要懂得這個演算法是如何來的？在哪裡應用以及侷限性，這樣才能靈活應用避免接觸的演算法多了變得一頭霧水，思路不清晰。

題外思考

貨幣的起源和其特性？
       這還要從歷史說起，回到遠古時代人們過著狩獵的生活，隨著生活有了規律屋子逐漸豐富起來，糧食等有了剩餘，但是發現缺少其它東西比如香皂等，這時人們就想將自家的糧食和別人交換，最開始只是拿一些易於儲存、有特徵的東西當做交換的憑證，比如大石頭，後來經過不斷髮展產生了大家公認的貨幣，其實貨幣概念要某個首領或者權威部門公式，只有大家都知道它代表這個等價的物品，別人才買你的賬，才可能和你交換，就如同現在的人民幣，再說說支付寶其實也是一個貨幣工作，在它裡面展示的只是一個數字而已，你卻可以用它來買賣這種東西，這種即貨幣的作用，其實貨幣正在向著數字化方向發展，我感覺自己已經很久沒有使用紙幣了，有時拿著一點也是為了手機沒電或者特殊情況備用，日常消費往往一部手機足以。
代表貨幣的工具、表現方式並不重要，重要的是它所公認的屬性所發揮的作用。