雜湊函式的構造方法
一個“好”的雜湊函式一般應考慮下列兩個因素:
- 計算簡單,以便提高轉換速度;
- 關鍵詞對應的地址空間分佈均勻,以儘量減少衝突。
1 數字關鍵詞的雜湊函式構造
1.1 直接定址法
取關鍵詞的某個線性函式值為雜湊地址,即
h(key) = a × key + b (a、b為常數)
地址 h(key) |
出生年月(key) |
人數(attribute) |
|---|---|---|
| 0 | 1900 | 1285萬 |
| 1 | 1901 | 1281萬 |
| 2 | 1902 | 1280萬 |
| …… | …… | …… |
| 10 | 2000 | 1250萬 |
| …… | …… | …… |
| 10 | 2011 | 1180萬 |
根據上表,得出雜湊函式的建構函式為:h(key)=key-1990
1.2 除留餘數法
雜湊函式為:h(key) = key mod p
例: h(key) = key % 17
| 地址 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 關鍵詞 | 34 | 18 | 2 | 20 | 23 | 7 | 42 | 27 | 11 | 30 | 15 |
一般,p 取素數,這裡:p = Tablesize = 17
1.3 數字分析法
分析數字關鍵字在各位上的變化情況,取比較隨機的位作為雜湊地址
比如:取11位手機號碼key的後4位作為地址:
雜湊函式為:h(key) = atoi(key+7) (char *key)

如果關鍵詞 key是18位的身份證號碼:
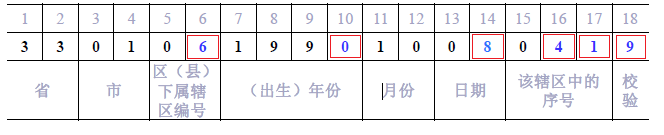
用紅線標出來的是變化比較大的的6位數字,這裡就取這6位數字來組建雜湊函式
h1(key) = (key[6]-‘0’)×104 + (key[10]-‘0’)×103 +(key[14]-‘0’)×102 + (key[16]-‘0’)×10 + (key[17]-‘0’)
當 key[18] = ‘x’時,身份證最後一位為X
h(key) = h1(key)×10 + 10
當 key[18] 為’0’~’9’時,身份證最後一位為數字
h(key) = h1(key)×10 + key[18]-‘0’
1.4 摺疊法
把關鍵詞分割成位數相同的幾個部分,然後疊加
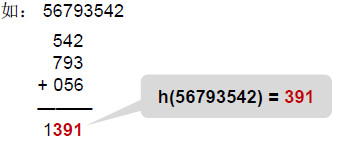
1.5 平方取中法
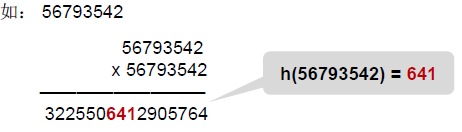
2 字元關鍵詞的雜湊函式構造
2.1 一個簡單的雜湊函式——ASCII碼加和法
對字元型關鍵詞key定義雜湊函式如下:
h(key) = (Σkey[i]) mod TableSize
問題:對於ASCII之和相同的字串就會衝突,比如a3、 b2、c1;eat、 tea;
2.2 簡單的改進——前3個字元移位法
把字串的前三個字元取出來,看成27進位制種的個位數,十位數,百位數,為什麼使用27,因為有26個字元,考錄空格,就是27。
h(key)=(key[0]×272 + key[1]×27 + key[2]) mod TableSize
問題:
1、仍然衝突:string、 street、strong、structure等等,前三個字元相同;
2、空間浪費:3000/263 ≈ 30%
前三個字元的不同組合在實際使用中大概有3000種可能,我們假設所有的字母(26個英文字母)排列組合有263種情況,散列表只用到30%。
2.3 好的雜湊函式——移位法
涉及關鍵詞所有n個字元,並且分佈得很好:
這裡就考慮這個字串的所有位。把它看成是32進位制數的每一位,為什麼是32進位制,後面會說。
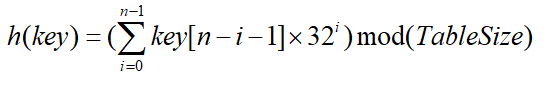
如何快速計算:
h(“abcde”)=‘a’*324+’b’*323+’c’*322+’d’*32+’e’
計算過程如下:
h=a
h=a * 32 + b
h=(a * 32 +b) * 32 + c
h=((a * 32 + b) * 32 + c) * 32 + d
h=(((a * 32 + b) * 32 + c) * 32 + d) * 32 + e
這裡a * 32 == a<<5,左移5位相當於乘以32
快速計算程式碼如下:
Index Hash(const char *Key, int TableSize)
{
unsigned int h = 0; //雜湊函式值,初始化為0
while (*Key != '\0') //位移對映
h = (h << 5) + *Key++;
return h % TableSize;
}
3 總結
- 數字關鍵詞的雜湊函式構造(1、直接定址法 2、除留餘數法 3、數字分析法 4、摺疊法 5、平方取中法)
- 字元關鍵詞的雜湊函式構造(1、ASCII碼加和法 2、前3個字元移位法 3、移位法)
