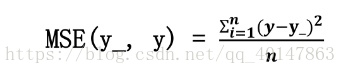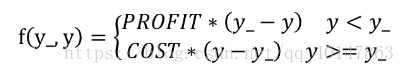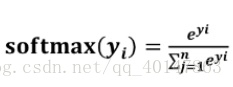2. 程式人生 > >TensorFlow筆記-06-神經網路優化-損失函式,自定義損失函式,交叉熵

TensorFlow筆記-06-神經網路優化-損失函式,自定義損失函式,交叉熵

阿新 • • 發佈：2018-12-09

TensorFlow筆記-06-神經網路優化-損失函式，自定義損失函式

  • **神經元模型：用數學公式比表示為：f(Σi xi*wi + b), f為啟用函式**
  • 神經網路 是以神經元為基本單位構成的
  • 啟用函式：引入非線性啟用因素，提高模型的表達能力 常用的啟用函式有relu、sigmoid、tanh等
  • (1)啟用函式relu：在Tensorflow中，用tf.nn.relu()表示 這裡寫圖片描述
  • (2)啟用函式sigmoid：在Tensorflow中，用tf.nn.sigmoid()表示 這裡寫圖片描述
  • (3)啟用函式tanh：在Tensorflow中，用tf.nn.tanh()表示 這裡寫圖片描述
  • 神經網路的複雜度：可用神經網路的的層數和神經網路中待優化引數個數表示
  • 神經網路的層數：一般不計入輸入層，層數 = n個隱藏層 + 1個輸入層
  • 神經網路待優化的引數：神經網路中所有引數w的個數 + 所有引數b的個數
  • 例如： 這裡寫圖片描述 在該神經網路中，包含1個輸入層，1個隱藏層和1個輸出層，該神經網路的引數為2層 在該神經網路中，引數的個數是所有引數w的個數加上所有引數b的總數，第一層引數用三行四列的二階張量表示（即12個線上的權重w）再加上4個偏置b；第二層引數是四行二列的二階張量（即8個線上的權重w）再加上2個偏置b 總引數 = 34+4 + 42+2 = 26

損失函式

  • 損失函式（loss）：用來表示預測（y）與已知答案（y_）的差距。在訓練神經網路時，通過不斷改變神經網路中所有引數，使損失函式不斷減小，從而訓練出更高準確率的神經網路模型
  • 常用的損失函式有均方誤差，自定義和交叉熵等
  • 均方誤差mse：n個樣本的預測值（y）與（y_）的差距。在訓練神經網路時，通過不斷的改變神經網路中的所有引數，使損失函式不斷減小，從而訓練出更高準確率的神經網路模型 這裡寫圖片描述
  • 在Tensorflow中用loss_mse = tf.reduce_mean(tf.square(y_-y))
  • 例如：
  • 預測酸奶日銷量y，x1和x2是兩個影響日銷量的因素
  • 應提前採集的資料有：一段時間內，每日的x1因素、x2因素和銷量y_。且資料儘量多
  • 在本例子中用銷量預測產量，最優的產量應該等於銷量，由於目前沒有資料集，所以擬造了一套資料集。利用Tensorflow中函式隨機生成x1、x2，製造標準答案y_ = x1 + x2，為了真實，求和後還加了正負0.05的隨機噪聲
  • 我們把這套自制的資料集喂入神經網路，構建一個一層的神經網路，擬合預測酸奶日銷量的函式
# coding:utf-8
# 預測多或者預測少的影響一樣
# 匯入模組，生成資料集
import tensorflow as tf
import numpy as np

# 一次喂入神經網路8組資料，數值不可以過大
BATCH_SIZE = 8
SEED = 23455

# 基於seed產生隨機數
rdm = np.random.RandomState(SEED)
# 隨機數返回32行2列的矩陣 表示32組 體積和重量 作為輸入資料集
X = rdm.rand(32, 2)
Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]
print("X:\n", X)
print("Y:\n", Y_)

# 定義神經網路的輸入，引數和輸出，定義前向傳播過程
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

# w1為2行1列
w1 = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)

# 定義損失函式及反向傳播方法
# 定義損失函式為MSE，反向傳播方法為梯度下降
loss_mse = tf.reduce_mean(tf.square(y_-y))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mse)
# 其他優化方法
# train_step = tf.train.GMomentumOptimizer(0.001, 0.9).minimize(loss_mse)
# train_step = tf.train.AdamOptimizer(0.001).minimize(loss_mse)

# 生成會話，訓練STEPS輪
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)

    # 訓練模型20000輪
    STEPS = 20000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 32
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
        # 沒500輪列印一次loss值
        if i % 1000 == 0:
            total_loss = sess.run(loss_mse, feed_dict={x: X, y_: Y_})
            print("After %d training step(s), loss on all data is %g" %(i, total_loss))
            print(sess.run(w1),"\n")

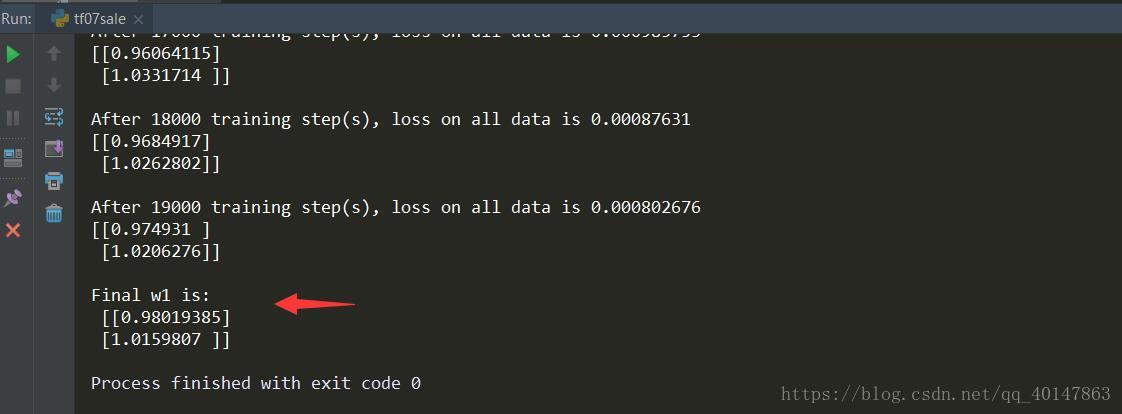
    print("Final w1 is: \n", sess.run(w1))

執行結果

這裡寫圖片描述

結果分析

有上述程式碼可知，本例中神經網路預測模型為y = w1x1 + w2x2，損失函式採用均方誤差。通過使損失函式值（loss）不斷降低，神經網路模型得到最終引數w1 = 0.98，w2 = 1.02，銷量預測結果為y = 0.98x1 + 1.02x2。由於在生成資料集時，標準答案為y = x1 + x2，因此，銷量預測結果和標準答案已經非常接近，說明該神經網路預測酸奶日銷量正確

自定義損失函式

  • 自定義損失函式：根據問題的實際情況，定製合理的損失函式
  • 例如：
    • 對於預測酸奶日銷量問題，如果預測銷量大於實際銷量則會損失成本；如果預測銷量小於實際銷量則會損失利潤。在實際生活中，往往製造一盒酸奶的成本和銷售一盒酸奶的利潤不是等價的。因此，需要使用符合該問題的自定義損失函式
    • 自定義損失函式為：loss = Σnf(y_, y)
    • 其中，損失函式成分段函式： 這裡寫圖片描述
    • 損失函式表示
      • 若預測結果y小於標準答案y_，損失函式為利潤乘以預測結果y與標準答案之差
      • 若預測結果y大於標準答案y_，損失函式為成本乘以預測結果y與標準答案之差

用Tensorflow函式表示為：

  • loss = tf.reduce_sum(tf.where(tf.greater(y, y_), COST(y-y_), PROFIT(y_-y)))

(1)第1種情況：若酸奶成本為1元，酸奶銷售利潤為9元，則製造成本小於酸奶利潤，因此希望預測結果y多一些。採用上述的自定義損失函式，訓練神經網路模型

# 第一種情況：酸奶成本1元，酸奶利潤9元
# 預測少了損失大，故不要預測少，故生成的模型會多預測一些
# 匯入模組，生成資料集
import tensorflow as tf
import numpy as np

# 一次喂入神經網路8組資料，數值不可以過大
BATCH_SIZE = 8
SEED = 23455
COST = 1
PROFIT = 9

# 基於seed產生隨機數
rdm = np.random.RandomState(SEED)
# 隨機數返回32行2列的矩陣 表示32組 體積和重量 作為輸入資料集
X = rdm.rand(32, 2)
Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]

# 定義神經網路的輸入，引數和輸出，定義前向傳播過程
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

# w1為2行1列
w1 = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)

# 定義損失函式及反向傳播方法
# 定義損失函式使得預測少了的損失大，於是模型應該偏向多的放心預測
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), COST*(y-y_), PROFIT*(y_-y)))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
# 其他優化方法
# train_step = tf.train.GMomentumOptimizer(0.001, 0.9).minimize(loss)
# train_step = tf.train.AdamOptimizer(0.001).minimize(loss)

# 生成會話，訓練STEPS輪
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)

    # 訓練模型20000輪
    STEPS = 20000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 32
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
        # 沒500輪列印一次loss值
        if i % 1000 == 0:
            total_loss = sess.run(loss, feed_dict={x: X, y_: Y_})
            print("After %d training step(s), loss on all data is %g" %(i, total_loss))
            print(sess.run(w1),"\n")

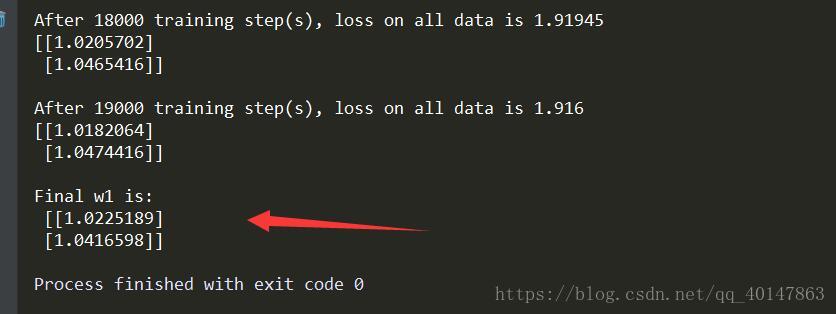
    print("Final w1 is: \n", sess.run(w1))

執行結果

這裡寫圖片描述

執行結果分析

由程式碼執行結果可知，神經網路最終引數為w1=1.03，w2=1.05，銷量預測結果為y = 1.03x1 + 1.05x2。由此可見，採用自定義損失函式預測的結果大於採用均方誤差的結果，更符合實際需求

(2)第2種情況：若酸奶成本為9元，酸奶銷售利潤為1元，則製造利潤小於酸奶成本，因此希望預測結果y小一些。採用上述的自定義損失函式，訓練神經網路模型

# 第二種情況：酸奶成本9元，酸奶利潤1元
# 預測多了損失大，故不要預測多，故生成的模型會少預測一些
# 匯入模組，生成資料集
import tensorflow as tf
import numpy as np

# 一次喂入神經網路8組資料，數值不可以過大
BATCH_SIZE = 8
SEED = 23455
COST = 9
PROFIT = 1

# 基於seed產生隨機數
rdm = np.random.RandomState(SEED)
# 隨機數返回32行2列的矩陣 表示32組 體積和重量 作為輸入資料集
X = rdm.rand(32, 2)
Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]

# 定義神經網路的輸入，引數和輸出，定義前向傳播過程
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

# w1為2行1列
w1 = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)

# 定義損失函式及反向傳播方法
# 重新定義損失函式使得預測多了的損失大，於是模型應該偏向少的方向預測
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), COST*(y-y_), PROFIT*(y_-y)))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
# 其他優化方法
# train_step = tf.train.GMomentumOptimizer(0.001, 0.9).minimize(loss)
# train_step = tf.train.AdamOptimizer(0.001).minimize(loss)

# 生成會話，訓練STEPS輪
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)

    # 訓練模型20000輪
    STEPS = 20000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 32
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
        # 沒500輪列印一次loss值
        if i % 1000 == 0:
            total_loss = sess.run(loss, feed_dict={x: X, y_: Y_})
            print("After %d training step(s), loss on all data is %g" %(i, total_loss))
            print(sess.run(w1),"\n")

    print("Final w1 is: \n", sess.run(w1))

執行結果

這裡寫圖片描述

執行結果分析

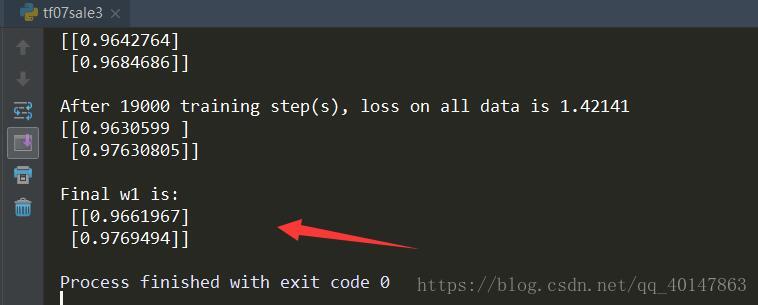
由執行結果可知，神經網路最終引數為w1 = 0.96，w2 = 0.97，銷量預測結果為y = 0.96+x1 + 0.7*x2。 因此，採用自定義損失函式預測的結果小於採用均方誤差預測得結果，更符合實際需求

交叉熵

  • 交叉熵（Cross Entropy）：表示兩個概率分佈之間的距離，交叉熵越大，兩個概率分佈距離越遠，兩個概率分佈越相異；交叉熵越小，兩個概率分佈距離越近，兩個概率分佈越相似
  • 交叉熵計算公式：H(y_, y) = -Σy_ * log y

  • 用 Tensorflow 函式表示

    ce = -tf.reduce_mean(y_*tf.clip_by_value(y, le-12, 1.0)))

  • 例如： 兩個神經網路模型解決二分類問題中，已知標準答案為 y_ = (1, 0)，第一個神經網路模型預測結果為 y1 = (0.6, 0.4)，第二個神經網路模型預測結果為 y2 = (0.8, 0.2)，判斷哪個神經網路模型預測得結果更接近標準答案

  • 根據交叉熵的計算公式得：

    H(1, 0), (0.6, 0.4) = -(1 * log0.6 + 0log0.4) ≈ -(-0.222 + 0) = 0.222 H(1, 0), (0.8, 0.2) = -(1 log0.8 + 0*log0.2) ≈ -(-0.097 + 0) = 0.097

softmax 函式

  • softmax 函式：將 n 分類中的 n 個輸出（y1, y2...yn）變為滿足以下概率分佈要求的函式: ∀x = P(X = x) ∈ [0, 1]
  • softmax 函式表示為： 這裡寫圖片描述
  • softmax 函式應用：在 n 分類中，模型會有 n 個輸出，即 y1，y2 ... n, 其中yi表示第 i 中情況出現的可能性大小。將 n 個輸出經過 softmax 函式，可得到符合概率分佈的分類結果

  • 在 Tensorflow 中，一般讓模型的輸出經過 softmax 函式，以獲得輸出分類的概率分佈再與標準答案對比，求出交叉熵，得到損失函式，用如下函式實現：

    ce = tf.nn.sparse_softmax_cross_entropy_with_logits(logits = y, labels = tf.argmax(y_, 1)) cem = tf.reduce_mean(ce)

  • 本筆記不允許任何個人和組織轉載

相關推薦

TensorFlow筆記-06-神經網路優化-損失函式,自定義損失函式,交叉熵

TensorFlow筆記-06-神經網路優化-損失函式，自定義損失函式 **神經元模型：用數學公式比表示為：f(Σi xi*wi + b), f為啟用函式** 神經網路 是以神經元為基本單位構成的 啟用函式：引入非線性啟用因素，提高模型的表達能力 常用的啟用函式有relu、sigmoid、tanh等 (1)

TensorFlow筆記-06-神經網絡優化-損失函數,自定義損失函數,交叉熵

dev rand() 所有 體積 sum 說明 where max ntop TensorFlow筆記-06-神經網絡優化-損失函數,自定義損失函數,交叉熵 神經元模型：用數學公式比表示為：f(Σi xi*wi + b), f為激活函數 神經網絡 是以神經元為基本單位構成

五、改進神經網路的學習方法（1）：交叉熵代價函式

本部落格主要內容為圖書《神經網路與深度學習》和National Taiwan University (NTU)林軒田老師的《Machine Learning》的學習筆記，因此在全文中對它們多次引用。初出茅廬，學藝不精，有不足之處還望大家不吝賜教。

Spring注入與無參建構函式自定義建構函式

在Java中，如果你自己寫了一個構造器，那麼Java機制將不會提供給你一個預設的構造器，除非你的類中無任何構造器時它才會提供預設的，但是Spring注入時，不管你是否新增屬性的注入，它都要去尋找預設構造器，為的是一旦你不注入屬性了，也能找到預設構造器，所以，規範的Java寫

TensorFlow北大公開課學習筆記4.4-神經網路優化----正則化 （正則化損失函式）

 今天學習了正則化，主要內容是：通過程式碼比較正則化與不正則化的區別。 什麼叫過擬合？           神經網路模型在訓練資料集上的準確率較高，在新的資料進行預測或分類時準確率較低， 說明模型的泛化能力差 什麼叫正則化：？           在損失函式中給每個引數

人工智慧實踐：TensorFlow筆記學習（四）—— 神經網路優化

神經網路優化 大綱4.1 損失函式4.2 學習率4.3 滑動平均4.4 正則化4.5 神經網路搭建八股目標掌握神經網路優化方法4.1 損失函式神經元模型：用數學公式表示為：，f為啟用函式。神經網路是以神經元為基本單元構成的。啟用函式：引入非線性啟用因素，提高模型的表達力。常用

tensorflow卷積神經網路例子學習筆記

tensorflow卷積神經網路例子 本文是對tensorflow教程中的cifar資料集卷積神經網路例子進行學習後的筆記，主要記錄了一些相關方法的使用。 模型輸入 模型的輸入包括input()、distorted_inputs等一些操作，分別

TensorFlow深度學習筆記 迴圈神經網路實踐

載入資料 使用text8作為訓練的文字資料集text8中只包含27種字元：小寫的從a到z，以及空格符。如果把它打出來，讀起來就像是去掉了所有標點的wikipedia。 直接呼叫lesson1中maybe_download下載text8.zip用zipfile讀取zip內容

深度學習筆記——TensorFlow學習筆記（三）使用TensorFlow實現的神經網路進行MNIST手寫體數字識別

本文是TensorFlow學習的第三部分，參考的是《TensorFlow實戰Google深度學習框架》一書，這部分講述的是使用TensorFlow實現的神經網路進行MNIST手寫體數字識別一個例項。 這個例項將第二部分講述的啟用函式、損失函式、優化演算法、正則化等都運用上了

【Tensorflow tf 掏糞記錄】筆記四——tensorflow搭建GAN神經網路

GAN，對抗神經網路。簡單通俗的說就是類似老頑童的左右互博術這種東西。機器試圖自己打敗自己，畢竟世界上最大的敵人是自己。哈哈哈哈。 2018/3/31 18:35 pm 下面是我最新訓練生成的結果，網路深度為512，個別的類似3，5，2的複雜的數我是用1

TensorFlow神經網路優化策略

在神經網路模型優化的過程中，會遇到許多問題，比如如何設定學習率的問題，我們可通過指數衰減的方式讓模型在訓練初期快速接近較優解，在訓練後期穩定進入最優解區域；針對過擬合問題，通過正則化的方法加以應對；滑動平均模型可以讓最終得到的模型在未知資料上表現的更加健壯。 一、學習率的設

tensorflow實現簡單神經網路層逼近一個二次函式的demo

  構造一個滿足一元二次函式y=a*x^2 + b的網路，生成一批原始資料，然後搭建簡單的神經網路，僅僅包含著一個輸入層、一個隱藏層和一個輸出層。通過TensorFlow吧隱藏層和輸出層的權重w和偏置

激勵函式簡介 Tensorflow最簡單的三層神經網路及matplotlib視覺化 附激勵函式常見型別

激勵函式： 有人說翻譯成“啟用函式”（activation function）會更好，因為主要作用是分割資料，判斷該“神經”是否被啟用。比如說，當你判斷面前的動物是否是一隻貓的時候，你會從各個部分去判斷。比如眼睛，當你覺得確實像貓的眼睛時，判斷眼睛的神經數值會特別高，如果覺

TensorFlow——卷積神經網路的相關函式

在TensorFlow中，使用tr.nn.conv2d來實現卷積操作，使用tf.nn.max_pool進行最大池化操作。通過闖傳入不同的引數，來實現各種不同型別的卷積與池化操作。 卷積函式tf.nn.conv2d TensorFlow裡使用tf.nn.conv2d函式來實現卷積，其格式如下： tf.nn

TensorFlow學習筆記——深層神經網路的整理

　　維基百科對深度學習的精確定義為“一類通過多層非線性變換對高複雜性資料建模演算法的合集”。因為深層神經網路是實現“多層非線性變換”最常用的一種方法，所以在實際中可以認為深度學習就是深度神經網路的代名詞。從維基百科給出的定義可以看出，深度學習有兩個非常重要的特性——多層和非線性。那麼為什麼要強調這兩個性質呢？

水電站入庫流量預測--基於自定義損失函式的迴圈神經網路建模方法

從志在必得到鎩羽而歸——記一次大資料競賽經歷 最近參加了一個比賽，在工業大資料產業創新平臺上，是一個水電站入庫流量預測問題。簡單看了一下題目，嚯，這個方向以前有做過啊，不說了~開整。 賽題背景：對進入水電站水庫的入庫流量進行精準預測，能夠幫助水電站對防洪、發電計劃排程工作進行合理安排。入庫流量受到降水、蒸發、

20180929 北京大學 人工智能實踐：Tensorflow筆記06

.com 分享 inf 智能 flow 人工智能 圖片 北京 技術分享 20180929 北京大學 人工智能實踐：Tensorflow筆記06

神經網路優化（二） - 滑動平均

1 滑動平均概述 滑動平均（也稱為 影子值 ）：記錄了每一個引數一段時間內過往值的平均，增加了模型的泛化性。 滑動平均通常針對所有引數進行優化：W 和 b， 簡單地理解，滑動平均像是給引數加了一個影子，引數變化，影子緩慢追隨。 滑動平均的表示公式為 影子 = 衰減率 * 影子 + ( 1 - 衰減率

神經網路優化（二） - 搭建神經網路八股

為提高程式的可複用性，搭建模組化的神經網路八股 1 前向傳播 前向傳播就是設計、搭建從輸入（引數 x ） 到輸出（返回值為預測或分類結果 y ）的完整網路結構，實現前向傳播過程，一般將其放在 forward.py 檔案中 前向傳播需要定義三個函式（實際上第一個函式是框架，第二、三個函式是賦初值過程）

Tensorflow實現單神經網路

#tensorflow實現模型評估 #訓練集 #測試集 #驗證集 import matplotlib.pyplot as plt import numpy as np import tensorflow as tf sess=tf.Session() #資料集準備 x_vals=n