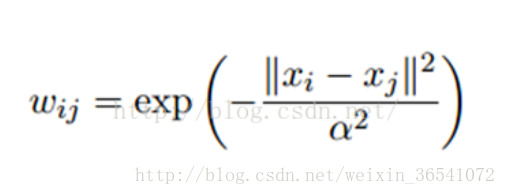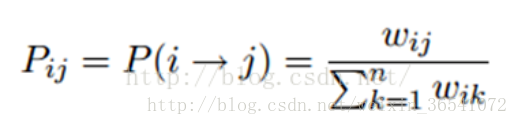社群發現演算法之標籤傳播(LPA)
標籤傳播演算法(LPA)的做法比較簡單:
第一步: 為所有節點指定一個唯一的標籤;
第二步: 逐輪重新整理所有節點的標籤,直到達到收斂要求為止。對於每一輪重新整理,節點標籤重新整理的規則如下:
對於某一個節點,考察其所有鄰居節點的標籤,並進行統計,將出現個數最多的那個標籤賦給當前節點。當個數最多的標籤不唯一時,隨機選一個。
- 1
注:演算法中的記號 N_n^k 表示節點 n 的鄰居中標籤為 k 的所有節點構成的集合。
標籤傳播演算法(label propagation)的核心思想非常簡單:相似的資料應該具有相同的label。LP演算法包括兩大步驟:1)構造相似矩陣;2)勇敢的傳播吧。
LP演算法是基於Graph的,因此我們需要先構建一個圖。我們為所有的資料構建一個圖,圖的節點就是一個數據點,包含labeled和unlabeled的資料。節點i和節點j的邊表示他們的相似度。這個圖的構建方法有很多,這裡我們假設這個圖是全連線的,節點i和節點j的邊權重為:
這裡,α是超參。
還有個非常常用的圖構建方法是knn圖,也就是隻保留每個節點的k近鄰權重,其他的為0,也就是不存在邊,因此是稀疏的相似矩陣。
- 1
標籤傳播演算法非常簡單:通過節點之間的邊傳播label。邊的權重越大,表示兩個節點越相似,那麼label越容易傳播過去。我們定義一個NxN的概率轉移矩陣P:
Pij表示從節點i轉移到節點j的概率。假設有C個類和L個labeled樣本,我們定義一個LxC的label矩陣YL,第i行表示第i個樣本的標籤指示向量,即如果第i個樣本的類別是j,那麼該行的第j個元素為1,其他為0。同樣,我們也給U個unlabeled樣本一個UxC的label矩陣YU。把他們合併,我們得到一個NxC的soft label矩陣F=[YL;YU]。soft label的意思是,我們保留樣本i屬於每個類別的概率,而不是互斥性的,這個樣本以概率1只屬於一個類。當然了,最後確定這個樣本i的類別的時候,是取max也就是概率最大的那個類作為它的類別的。那F裡面有個YU,它一開始是不知道的,那最開始的值是多少?無所謂,隨便設定一個值就可以了。
千呼萬喚始出來,簡單的LP演算法如下: 1)執行傳播:F=PF 2)重置F中labeled樣本的標籤:FL=YL 3)重複步驟1)和2)直到F收斂。 步驟1)就是將矩陣P和矩陣F相乘,這一步,每個節點都將自己的label以P確定的概率傳播給其他節點。如果兩個節點越相似(在歐式空間中距離越近),那麼對方的label就越容易被自己的label賦予,就是更容易拉幫結派。步驟2)非常關鍵,因為labeled資料的label是事先確定的,它不能被帶跑,所以每次傳播完,它都得迴歸它本來的label。隨著labeled資料不斷的將自己的label傳播出去,最後的類邊界會穿越高密度區域,而停留在低密度的間隔中。相當於每個不同類別的labeled樣本劃分了勢力範圍。
變身的LP演算法
我們知道,我們每次迭代都是計算一個soft label矩陣F=[YL;YU],但是YL是已知的,計算它沒有什麼用,在步驟2)的時候,還得把它弄回來。我們關心的只是YU,那我們能不能只計算YU呢?Yes。我們將矩陣P做以下劃分:
程式碼如下:
import time
import numpy as np
# return k neighbors index
def navie_knn(dataSet, query, k):
numSamples = dataSet.shape[0]
## step 1: calculate Euclidean distance
diff = np.tile(query, (numSamples, 1)) - dataSet
squaredDiff = diff ** 2
squaredDist = np.sum(squaredDiff, axis = 1) # sum is performed by row
## step 2: sort the distance
sortedDistIndices = np.argsort(squaredDist)
if k > len(sortedDistIndices):
k = len(sortedDistIndices)
return sortedDistIndices[0:k]
# build a big graph (normalized weight matrix)
def buildGraph(MatX, kernel_type, rbf_sigma = None, knn_num_neighbors = None):
num_samples = MatX.shape[0]
affinity_matrix = np.zeros((num_samples, num_samples), np.float32)
if kernel_type == 'rbf':
if rbf_sigma == None:
raise ValueError('You should input a sigma of rbf kernel!')
for i in xrange(num_samples):
row_sum = 0.0
for j in xrange(num_samples):
diff = MatX[i, :] - MatX[j, :]
affinity_matrix[i][j] = np.exp(sum(diff**2) / (-2.0 * rbf_sigma**2))
row_sum += affinity_matrix[i][j]
affinity_matrix[i][:] /= row_sum
elif kernel_type == 'knn':
if knn_num_neighbors == None:
raise ValueError('You should input a k of knn kernel!')
for i in xrange(num_samples):
k_neighbors = navie_knn(MatX, MatX[i, :], knn_num_neighbors)
affinity_matrix[i][k_neighbors] = 1.0 / knn_num_neighbors
else:
raise NameError('Not support kernel type! You can use knn or rbf!')
return affinity_matrix
# label propagation
def labelPropagation(Mat_Label, Mat_Unlabel, labels, kernel_type = 'rbf', rbf_sigma = 1.5, \
knn_num_neighbors = 10, max_iter = 500, tol = 1e-3):
# initialize
num_label_samples = Mat_Label.shape[0]
num_unlabel_samples = Mat_Unlabel.shape[0]
num_samples = num_label_samples + num_unlabel_samples
labels_list = np.unique(labels)
num_classes = len(labels_list)
MatX = np.vstack((Mat_Label, Mat_Unlabel))
clamp_data_label = np.zeros((num_label_samples, num_classes), np.float32)
for i in xrange(num_label_samples):
clamp_data_label[i][labels[i]] = 1.0
label_function = np.zeros((num_samples, num_classes), np.float32)
label_function[0 : num_label_samples] = clamp_data_label
label_function[num_label_samples : num_samples] = -1
# graph construction
affinity_matrix = buildGraph(MatX, kernel_type, rbf_sigma, knn_num_neighbors)
# start to propagation
iter = 0; pre_label_function = np.zeros((num_samples, num_classes), np.float32)
changed = np.abs(pre_label_function - label_function).sum()
while iter < max_iter and changed > tol:
if iter % 1 == 0:
print "---> Iteration %d/%d, changed: %f" % (iter, max_iter, changed)
pre_label_function = label_function
iter += 1
# propagation
label_function = np.dot(affinity_matrix, label_function)
# clamp
label_function[0 : num_label_samples] = clamp_data_label
# check converge
changed = np.abs(pre_label_function - label_function).sum()
# get terminate label of unlabeled data
unlabel_data_labels = np.zeros(num_unlabel_samples)
for i in xrange(num_unlabel_samples):
unlabel_data_labels[i] = np.argmax(label_function[i+num_label_samples])
return unlabel_data_labelsJBQkFCMA==/dissolve/70/gravity/SouthEast)測試程式碼:
import time import math import numpy as np from labelPropagation import labelPropagation
def show(Mat_Label, labels, Mat_Unlabel, unlabel_data_labels): import matplotlib.pyplot as plt
for i in range(Mat_Label.shape[0]):
if int(labels[i]) == 0:
plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Dr')
elif int(labels[i]) == 1:
plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Db')
else:
plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Dy')
for i in range(Mat_Unlabel.shape[0]):
if int(unlabel_data_labels[i]) == 0:
plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'or')
elif int(unlabel_data_labels[i]) == 1:
plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'ob')
else:
plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'oy')
plt.xlabel('X1'); plt.ylabel('X2')
plt.xlim(0.0, 12.)
plt.ylim(0.0, 12.)
plt.show()
def loadCircleData(num_data): center = np.array([5.0, 5.0]) radiu_inner = 2 radiu_outer = 4 num_inner = num_data / 3 num_outer = num_data - num_inner
data = []
theta = 0.0
for i in range(num_inner):
pho = (theta % 360) * math.pi / 180
tmp = np.zeros(2, np.float32)
tmp[0] = radiu_inner * math.cos(pho) + np.random.rand(1) + center[0]
tmp[1] = radiu_inner * math.sin(pho) + np.random.rand(1) + center[1]
data.append(tmp)
theta += 2
theta = 0.0
for i in range(num_outer):
pho = (theta % 360) * math.pi / 180
tmp = np.zeros(2, np.float32)
tmp[0] = radiu_outer * math.cos(pho) + np.random.rand(1) + center[0]
tmp[1] = radiu_outer * math.sin(pho) + np.random.rand(1) + center[1]
data.append(tmp)
theta += 1
Mat_Label = np.zeros((2, 2), np.float32)
Mat_Label[0] = center + np.array([-radiu_inner + 0.5, 0])
Mat_Label[1] = center + np.array([-radiu_outer + 0.5, 0])
labels = [0, 1]
Mat_Unlabel = np.vstack(data)
return Mat_Label, labels, Mat_Unlabel
def loadBandData(num_unlabel_samples): #Mat_Label = np.array([[5.0, 2.], [5.0, 8.0]]) #labels = [0, 1] #Mat_Unlabel = np.array([[5.1, 2.], [5.0, 8.1]])
Mat_Label = np.array([[5.0, 2.], [5.0, 8.0]])
labels = [0, 1]
num_dim = Mat_Label.shape[1]
Mat_Unlabel = np.zeros((num_unlabel_samples, num_dim), np.float32)
Mat_Unlabel[:num_unlabel_samples/2, :] = (np.random.rand(num_unlabel_samples/2, num_dim) - 0.5) * np.array([3, 1]) + Mat_Label[0]
Mat_Unlabel[num_unlabel_samples/2 : num_unlabel_samples, :] = (np.random.rand(num_unlabel_samples/2, num_dim) - 0.5) * np.array([3, 1]) + Mat_Label[1]
return Mat_Label, labels, Mat_Unlabel
if name == “main“: num_unlabel_samples = 800 #Mat_Label, labels, Mat_Unlabel = loadBandData(num_unlabel_samples) Mat_Label, labels, Mat_Unlabel = loadCircleData(num_unlabel_samples)
## Notice: when use 'rbf' as our kernel, the choice of hyper parameter 'sigma' is very import! It should be
## chose according to your dataset, specific the distance of two data points. I think it should ensure that
## each point has about 10 knn or w_i,j is large enough. It also influence the speed of converge. So, may be
## 'knn' kernel is better!
#unlabel_data_labels = labelPropagation.labelPropagation(Mat_Label, Mat_Unlabel, labels, kernel_type = 'rbf', rbf_sigma = 0.2)
unlabel_data_labels = labelPropagation(Mat_Label, Mat_Unlabel, labels, kernel_type = 'knn', knn_num_neighbors = 10, max_iter = 400)
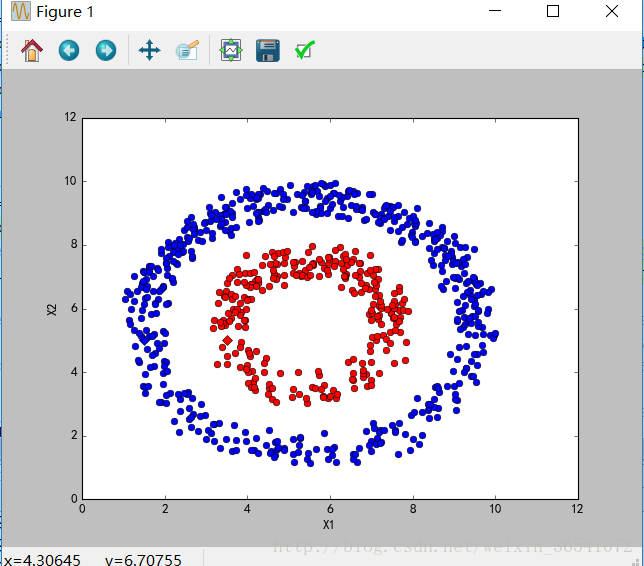
show(Mat_Label, labels, Mat_Unlabel, unlabel_data_labels)
結果如下:
利用networkx:
#coding:utf-8
'''
Created on 2017-1-4
@author: 劉帥
'''
import collections
import random
import networkx as nx
class LPA():
def __init__(self, G, max_iter = 20):
self._G = G
self._n = len(G.node) #number of nodes
self._max_iter = max_iter
def can_stop(self):
# all node has the label same with its most neighbor
for i in range(self._n):
node = self._G.node[i]
label = node["label"]
max_labels = self.get_max_neighbor_label(i)
if(label not in max_labels):
return False
return True
def get_max_neighbor_label(self,node_index):
m = collections.defaultdict(int)
for neighbor_index in self._G.neighbors(node_index):
neighbor_label = self._G.node[neighbor_index]["label"]
m[neighbor_label] += 1
max_v = max(m.itervalues())
return [item[0] for item in m.items() if item[1] == max_v]
'''asynchronous update'''
def populate_label(self):
#random visit
visitSequence = random.sample(self._G.nodes(),len(self._G.nodes()))
for i in visitSequence:
node = self._G.node[i]
label = node["label"]
max_labels = self.get_max_neighbor_label(i)
if(label not in max_labels):
newLabel = random.choice(max_labels)
node["label"] = newLabel
def get_communities(self):
communities = collections.defaultdict(lambda:list())
for node in self._G.nodes(True):
label = node[1]["label"]
communities[label].append(node[0])
return communities.values()
def execute(self):
#initial label
for i in range(self._n):
self._G.node[i]["label"] = i
iter_time = 0
#populate label
while(not self.can_stop() and iter_time<self._max_iter):
self.populate_label()
iter_time += 1
return self.get_communities()
if __name__ == '__main__':
G = nx.karate_club_graph()
algorithm = LPA(G)
communities = algorithm.execute()
for community in communities:
print community結果如下:
[0, 1, 3, 7, 11, 12, 13, 17, 19, 21]
[5, 6, 16]
[4, 10]
[2, 8, 9, 14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]