4. 二維陣列中的查詢

題目描述：
在一個二維陣列中，每一行都按照從左到右遞增的順序排序，每一列都按照從上到下遞增的順序排序。請完成一個函式，輸入這樣的一個二維陣列和一個整數，判斷陣列中是否含有該整數。

解題思路：
我們知道這個二維資料的規律了，所以我們可以從右上角的那個數著手來，從右上角開始查詢。矩陣中的一個數，它左邊的數都比它小，下邊的數都比它大。因此，從右上角開始查詢，就可以根據 target 和當前元素的大小關係來縮小查詢區間。
複雜度：O(M + N) + O(1)
程式碼：

public boolean Find(int target, int[][] matrix) {
    if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
        return false;
    int rows = matrix.length, cols = matrix[0].length;
    int r = 0, c = cols - 1; // 從右上角開始
    while (r <= rows - 1 && c >= 0) {
        if (target == matrix[r][c])
            return true;
        else if (target > matrix[r][c])
    //如果target數大於最右邊的數，肯定要換下一行，
  //因為l連最右邊的數都小於target，所以左邊的數肯定都小於target
  //先判斷行，再判斷列。從上到下，從右至左
            r++;
        else
            c--;
    }
    return false;
}
 

5. 替換空格

題目描述
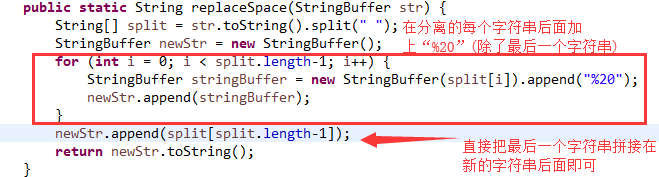
請實現一個函式，將一個字串中的每個空格替換成“%20”。例如，當字串為We Are Happy.則經過替換之後的字串為We%20Are%20Happy。

6. 從尾到頭列印連結串列

ListNode是由自己定義的java中的連結串列物件
類結構如下:

第一種解法：
遞迴思想：


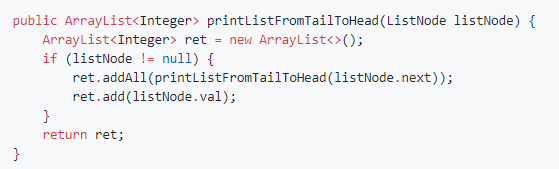
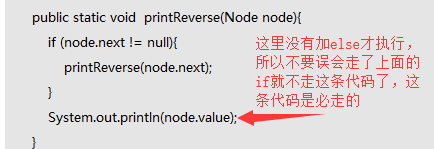
第二種解法：
非遞迴：利用棧（利用棧的“先進後出”特性）

7. 重建二叉樹（筆者對這個題還是有點小疑問）

題目描述
根據二叉樹的前序遍歷和中序遍歷的結果，重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重複的數字。
例如：

解題思路：
前序遍歷的第一個值為根節點的值，使用這個值將中序遍歷結果分成兩部分，左部分為樹的左子樹中序遍歷結果，右部分為樹的右子樹中序遍歷的結果。

// 快取中序遍歷陣列每個值對應的索引（這個陣列貫穿全部過程）
private Map<Integer, Integer> indexForInOrders = new HashMap<>();

public TreeNode reConstructBinaryTree(int[] pre, int[] in) {//？？？那這個pre到底傳中序還是前序呢????????
    for (int i = 0; i < in.length; i++)
        indexForInOrders.put(in[i], i);
    return reConstructBinaryTree(pre, 0, pre.length - 1, 0);
}

private TreeNode reConstructBinaryTree(int[] pre, int preL, int preR, int inL) {
    if (preL > preR)
        return null;
    TreeNode root = new TreeNode(pre[preL]);//前序遍歷的第一個值就是根節點
    int inIndex = indexForInOrders.get(root.val);
    int leftTreeSize = inIndex - inL;
    root.left = reConstructBinaryTree(pre, preL + 1, preL + leftTreeSize, inL);
    root.right = reConstructBinaryTree(pre, preL + leftTreeSize + 1, preR, inL + leftTreeSize + 1);
    return root;
}
 

8. 二叉樹的下一個結點

題目描述：
給定一個二叉樹和其中的一個結點，請找出中序遍歷順序的下一個結點並且返回。注意，樹中的結點不僅包含左右子結點，同時包含指向父結點的指標
節點的結構如下：

解題思路：
① 如果一個節點的右子樹不為空，那麼該節點的下一個節點是右子樹的最左節點；

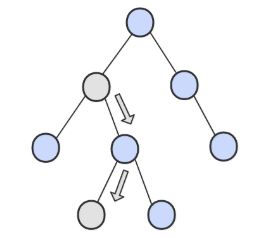
② 否則，向上找第一個左連結指向的樹包含該節點的祖先節點。

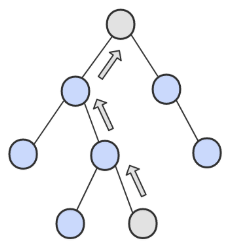
程式碼如下：

9. 用兩個棧實現佇列

題目描述：
用兩個棧來實現一個佇列，完成佇列的 Push 和 Pop 操作。

解題思路：
劍指offer的思路，用兩個棧來實現佇列，棧1的話用來入隊，佇列每進入一個元素就入棧1，棧2的話用來出隊，佇列如果要出隊，首先判斷棧2是不是空，是空，就把棧1彈出來進入棧2（因為棧是先入後出，兩次先入後出就是先入先出了，負負得正嘛~），然後從棧2開始彈，如果棧2不為空，直接從棧2開始彈
原始碼如下：

10.1 斐波那契數列

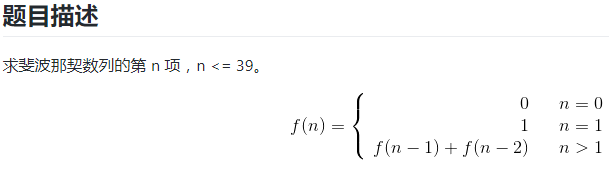
解題思路：
如果使用遞迴求解，會重複計算一些子問題。例如，計算 f(10) 需要遞迴計算 f(9) 和 f(8)，計算 f(9) 需要遞迴計算 f(8) 和 f(7)，可以看到 f(8) 被重複遞迴計算了。（解釋：你想想，計算f(10)的時候f(8)已經被遞迴了，f(9)又要遞迴f(8)有必要嗎？直接用剛才遞迴的結果就好啦）

解題思路：
遞迴是將一個問題劃分成多個子問題求解，動態規劃也是如此，但是動態規劃會把子問題的解快取起來，從而避免重複求解子問題。

優化方案：
考慮到第 i 項只與第 i-1 和第 i-2 項有關，因此只需要儲存前兩項的值就能求解第 i 項，從而將空間複雜度由 O(N) 降低為 O(1)。

由於題目中待求解的 n 小於 40，因此可以將前 40 項的結果先進行計算，之後就能以 O(1) 時間複雜度得到第 n 項的值了。

10.2 跳臺階

題目描述：
一隻青蛙一次可以跳上 1 級臺階，也可以跳上 2 級。求該青蛙跳上一個 n 級的臺階總共有多少種跳法。
解題思路：
解釋：之所以return的是target-1和target-2是因為跳到第n階臺階的最後一跳可能1步或者是2步，只有這兩種可能，所以只需要把JumpFloor(target-1)+JumpFloor(target-2)算出來就可以得到總結果

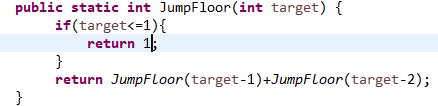
從上面明顯看出是斐波那契數列，所以還可以用下面的寫法

10.3 矩形覆蓋（小疑問：筆者也不是很明白這個題為什麼跟斐波那契數列掛鉤的）

題目描述：
我們可以用 21 的小矩形橫著或者豎著去覆蓋更大的矩形。請問用 n 個 21 的小矩形無重疊地覆蓋一個 2*n 的大矩形，總共有多少種方法？
程式碼如下：

10.4 變態跳臺階

題目描述：
一隻青蛙一次可以跳上 1 級臺階，也可以跳上 2 級… 它也可以跳上 n 級。求該青蛙跳上一個 n 級的臺階總共有多少種跳法。
解題思路：
跳到終點的最後一次跳可能是1級，也可能是2級，3，4，5…n
那麼f(n)=f(n-1)+f(n-2)+f(n-3)+…+f(n-n),
按這個公式推出f(n-1)=f((n-1)-1)+f((n-1)-2)+…+f((n-1)-(n-1))=f(n-2)+f(n-3)+…f(n-n);
將上面兩個式子相減得出f(n)=2*f(n-1),所以就有結論了