SLAM學習小組 : 視覺SLAM十四講 第三講 + 視覺SLAM理論與實踐 第二節
一、熟悉Eigen矩陣運算
Wiki Eigen
設線性⽅程 Ax = b,在 A 為⽅陣的前提下,請回答以下問題:
1. 在什麼條件下,x 有解且唯⼀?
線性方程組的矩陣滿秩(非奇異矩陣)
2. 高斯消元法的原理是什麼?
高斯消元法是將方程組中的一方程的未知數用含有另一未知數的代數式表示,並將其代人到另一方程中,這就消去了一未知數,得到一解;或將方程組中的一方程倍乘某個常數加到另外一方程中去,也可達到消去一未知數的目的。消元法主要用於二元一次方程組的求解。
在用係數矩陣表示的線性方程組中,高斯消元的過程就是將原來係數矩陣化為上三角矩陣的過程。主要是用初等變換將某一行倍乘後加到另一行,從而在下三角部分引入零元,變換以後所得線性代數方程組係數矩陣為上三角,很容易用回代求解。
4. QR 分解的原理是什麼?
如果實(復)非奇異矩陣A能夠化成正交(酉)矩陣Q與實(復)上三角矩陣R的乘積,即A=QR,則稱其為A的QR分解。(列滿秩矩陣必有QR分解)(當要求R的對角線元素為正時,該分解唯一)
其中Q的列向量是A的列空間的標準正交基,R是一個非奇異可逆的上三角矩陣
5. Cholesky 分解的原理是什麼?
Cholesky 分解是把一個對稱正定的矩陣表示成一個下三角矩陣L和其轉置的乘積的分解。它要求矩陣的所有特徵值必須大於零,故分解的下三角的對角元也是大於零的。Cholesky分解法又稱平方根法,是當A為實對稱正定矩陣時,LU三角分解法的變形。
6. 程式設計實現 A 為 100 × 100 隨機矩陣時,⽤ QR 和 Cholesky 分解求 x 的程式。你可以參考本次課用到的 useEigen 例程。
執行環境QT creator
#include <iostream>
using namespace std;
#include <ctime>
// Eigen 部分
#include <eigen3/Eigen/Core>
// 稠密矩陣的代數運算(逆,特徵值等)
#include <eigen3/Eigen/Dense>
#define MATRIX_SIZE 100
/****************************
* 本程式演示了 Eigen 基本型別的使用
****************************/
int main QR:
 Cholesky:
Cholesky:

提⽰:你可能需要參考相關的數學書籍或⽂章。請善⽤搜尋引擎。Eigen 固定⼤⼩矩陣最⼤⽀持到 50,
所以你會⽤到動態⼤⼩的矩陣。
二、幾何運算練習
執行環境QT creator
#include <iostream>
#include <cmath>
using namespace std;
#include <eigen3/Eigen/Core>
// Eigen 幾何模組
#include <eigen3/Eigen/Geometry>
/****************************
* 本程式演示了 Eigen 幾何模組的使用方法
****************************/
int main ( int argc, char** argv )
{
Eigen::Quaterniond q1(0.55,0.3,0.2,0.2);
Eigen::Quaterniond q2(-0.1,0.3,-0.7,0.2);
q1= q1.normalized();
q2= q2.normalized();
Eigen::Matrix3d R_ = q1.matrix().inverse();
Eigen::Matrix3d R2 = q2.matrix();
Eigen::Matrix<double,3,1> P1;
Eigen::Matrix<double,3,1> P2;
Eigen::Matrix<double,3,1> t1;
Eigen::Matrix<double,3,1> t2;
P1 << 0.5,-0.1,0.2;
t1 << 0.7,1.1,0.2;
t2 << -0.1,0.4,0.8;
P2 = R2 * R_ * (P1-t1) + t2;
cout<<"quaternion = \n"<<P2 <<endl; // 請注意coeffs的順序是(x,y,z,w),w為實部,前三者為虛部
// cout<<"quaternion = \n"<<t1 <<endl; // 請注意coeffs的順序是(x,y,z,w),w為實部,前三者為虛部
// cout<<"quaternion = \n"<<t2 <<endl; // 請注意coeffs的順序是(x,y,z,w),w為實部,前三者為虛部
// cout<<"quaternion = \n"<<R_ <<endl; // 請注意coeffs的順序是(x,y,z,w),w為實部,前三者為虛部
return 0;
}

三、 旋轉的表達
證明:
- 設有旋轉矩陣 R,證明 R T R = I 且 det R = +1
旋轉矩陣是由三個正交的單位向量定義的所以它是正交矩陣,因為是正交矩陣所以它的轉置等於它的逆,所以RTR=I
正交變換的矩陣的行列式等於1或-1,規定行列式等於1正交變換稱為旋轉變換,行列式等於-1正交變換稱為鏡面反射,所以“旋轉變換的矩陣的行列式為+1” - 設有四元數 q,我們把虛部記為 ε,實部記為 η,那麼 q = (ε, η)。請說明 ε 和 η 的維度。
ε虛部:三維
η實部:一維 - 定義運算
+和⊕為:

其中x含義與^相同,即取ε的反對稱矩陣(它們都成叉積的矩陣運算形式),1為單位矩陣。請證明對任意單位四元數 q 1 , q 2 ,四元數乘法可寫成矩陣乘法:
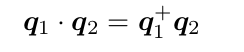
或
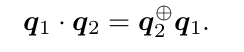
證:

四、 羅德里格斯公式的證明
羅德里格斯公式描述了從旋轉向量到旋轉矩陣的轉換關係。設旋轉向量長度為 θ,方向為 n,那麼旋轉矩陣 R 為:
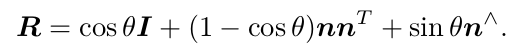
參考https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula
證:
 旋轉前根據矩陣投影公式可得:
旋轉前根據矩陣投影公式可得:
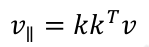
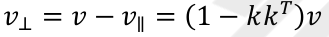
則旋轉後向量為:
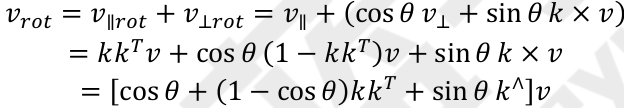
則旋轉矩陣為:

五、四元數運算性質的驗證
證明p ′ = qpq (−1) 是虛四元數;此外,上式亦可寫成矩陣運算:p ′ = Qp。請根據你的推導,給出矩陣 Q。注意此時 p 和 p ′ 都是四元數形式的變數,所以 Q 為 4 × 4 的矩陣。
設:
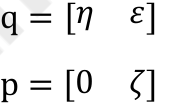
有:
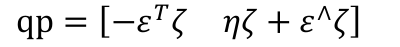
又有:
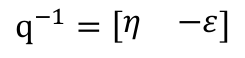
qpq (−1)的實部為:
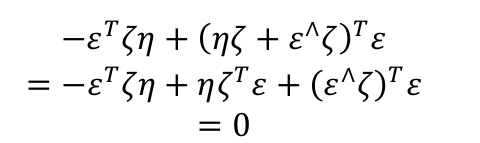
qpq (−1)的虛部為:
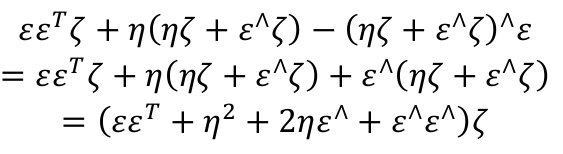
R為:
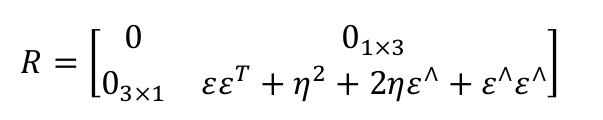
六、 熟悉C++11
 for:區間迭代
for:區間迭代
auto&:自動推導型別
[](const A&a1,const A&a2) {return a1.index<a2.index;}}:lambda函式
