2018-12-09 16:40:30

問題描述：

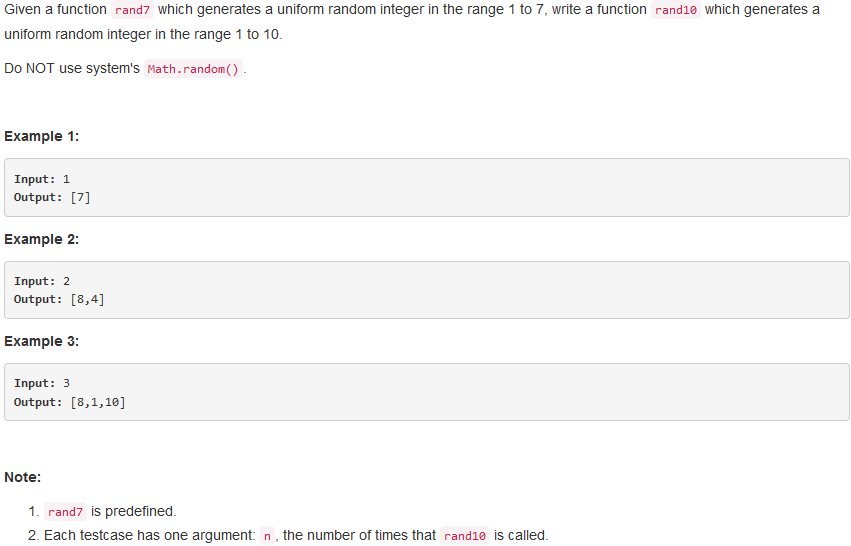
問題求解：

這個問題位元組跳動演算法崗面試有問到類似的，有rand6，求rand8，我想了好久，最後給了一個特殊解法，就進行三次，每次取前三個數和後三個數的概率相等為1 / 2，那麼最後需要得到的概率是1 / 8，就可以通過取三次得到。問題就轉變成了對映的問題，當然對映的方式是很簡單的，類似二進位制的方法，很容易就可以進行對映。

但是，上述的解法在本題中是沒有辦法使用的，就需要更通用的解法，說實話，之前也沒有做過Rejection Sampling標籤下的題目，這個問題的通用解法就是使用拒絕取樣的演算法來進行解決。

首先我們肯定是需要對原空間進行擴充的，因為原空間的大小比生成空間的大小要小。

我其實最初想到的也是兩次求rand7()，然後直接求和，但是很顯然的這樣得到的解空間中的1 - 10是不平均分配的，即使通過對10取餘 + 1也不能得到等概率的解。

當然還有人可能會想通過求乘積的方式來擴充空間，可惜的是這樣也是非等概率的，具體可以見下圖：

那麼怎麼樣才能得到等概率的呢？其實，我們只需要對兩次取得的各個可能的數進行編號，每個編號不就是等可能的麼？

由於編號的總長度大於10的倍數，後面的49 - 40 = 9個數字就需要拋棄掉。通過這種方式，我們就可以等概率的生成1 - 10這10個整數。

/**
 * The rand7() API is already defined in the parent class SolBase.
 * public int rand7();
 * @return a random integer in the range 1 to 7
 */
class Solution extends SolBase {
    public int rand10() {
        int res = Integer.MAX_VALUE;
        while (res >= 40) {
            res = 7 * (rand7() - 1) + rand7() - 1;
        }
        return res % 10 + 1;
    }
}