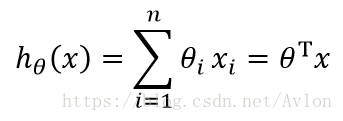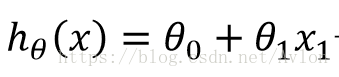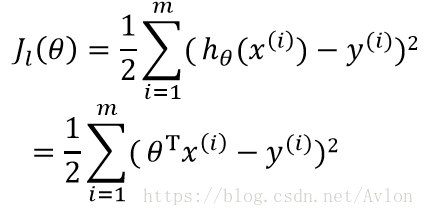ML課上老師佈置的第一個作業，利用線性迴歸預測南京房價，具體任務和資料如下圖所示：

首先我們可以很簡單的看出這是一個遞增的序列，所以2014年的價格大致應該是在13左右，這有助於我們除錯程式。

所謂線性迴歸就是用一條直線去擬合數據的關係，其擬合結果的理想情況當然是所有的資料點都能落到模型擬合的直線上，當然這基本是不可能的，線性迴歸的假設（或者說模型）便由下面這個公式表述：

在我們這個問題中因為x只有一維所以其模型為直線方程：

這裡你可以在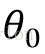旁乘上一個恆為1的x0這樣，便將偏置和其他引數統一化，也可以寫成上述的矩陣形式。為了衡量我們的模型的好壞，我們使用每個樣本點與預測點的歐氏距離的和作為代價函式（損失函式）即：

常係數是為了求導方便，有沒有都無所謂，當代價函式取到最小值時我們可以認為我們的模型達到了最佳擬合。這裡使用梯度下降法來進行最優化，梯度的求法見下式：

則引數的更新見下式：

這裡a是學習率，這個公式主要用來更新θ1，偏置θ0需要再對θ0求偏導，梯度結果就是”誤差“的和，不用乘上特徵。

按照上述過程，寫出程式就好，因為問題比較簡單這裡就不做可視化了。首先是我手寫的梯度下降：

資料存放在data.txt中，如下

這裡需要注意的是要對x（年份）進行標準化，原因不太明白，一般認為標準化是因為兩個特徵的取值範圍不同，這裡只有一個特徵不太明白為啥要標準化，不標準化的話會梯度爆炸，學習率設為0.0001一樣爆炸。這裡可以用numpy的矩陣操作，我嫌麻煩沒用，其實用熟練了的話會更簡潔。

import numpy as np
bias = 1
w = 1
learn_rate = 0.1
data_set = np.loadtxt("data.txt")

x = data_set[0:1, :]
x = np.array(x)
x = x.reshape(-1, 1)
y = data_set[1:, :]
y = np.array(y)
y = y.reshape(-1, 1)
mean = np.mean(x)
variance = np.std(x)

for i in range(14):         # 量化為標準高斯分佈
    x[i] = (x[i]-mean)/variance

old_loss = 0
loss = 0

for i in range(14):
    loss += (x[i]*w+bias-y[i])*(x[i]*w+bias-y[i])

while abs(loss - old_loss) > 0.00001:
    dew = 0
    for i in range(14):                # 計算θ1梯度
        dew += (x[i]*w-y[i])*x[i]
    w = w - dew*learn_rate
    dew = 0
    for i in range(14):                # 計算θ0梯度
        dew += (x[i]*w+bias-y[i])
    bias = bias - dew*learn_rate
    old_loss = loss
    loss = 0
    for i in range(14):
        loss += (x[i]*w+bias-y[i])*(x[i] * w +bias- y[i])
    print(old_loss)
print(((2014-mean)/variance)*w+bias)
 

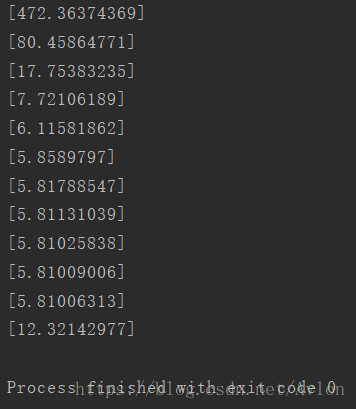
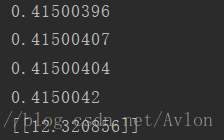
執行結果如下：

可以看到大概6步就已經收斂了，最後的預測結果是12.321

然後為了驗證也順便寫了個tensorflow版本的，給出程式碼：

import tensorflow as tf
import numpy as np

data_set = np.loadtxt("data.txt")

x = data_set[0:1, :]
x = np.array(x)
x = x.reshape(-1, 1)
y = data_set[1:, :]
y = np.array(y)
y = y.reshape(-1, 1)
mean = np.mean(x)
variance = np.std(x)

for i in range(14):         # 量化為標準高斯分佈
    x[i] = (x[i]-mean)/variance
input = tf.placeholder("float", [None, 1])
label = tf.placeholder("float", [None, 1])

v = tf.Variable(tf.zeros([1, 1]), dtype=tf.float32)
b = tf.Variable(0.0, dtype=tf.float32)

y_ = input*v+b

loss = tf.reduce_mean(tf.squared_difference(label, y_))

opt = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

init = tf.global_variables_initializer()

sess = tf.Session()

answer = v*((2014-mean)/variance)+b
sess.run(init)

for i in range(50):
    train, loss_value = sess.run([opt, loss], feed_dict={input: x, label: y})
    print(loss_value)
print(sess.run(answer))

結果：

結果差不多，說明原來手寫的正確。

tensorflow和手寫版的不同在於loss函式最後用的是求和再求平均的reduce_mean函式，用reduce_sum的話標準梯度下降不收斂（學習率0.1），這裡不太理解原因，手寫版中對梯度和loss做除13的操作後和tensorflow的結果一致，只是常數項的放大，為何到了tensorflow就不收斂這個問題不太清楚，望有大神解答。

其次做了幾個有趣的實驗，首先若不對x進行歸一化，用adam優化法是可以收斂的，最後的預測結果是6.35這正好和無偏置的預測模型的結果一致，這裡也搞不清楚原因

其次若使用reduce_sum來求最後的loss的話用adam在學習率為1的情況下也能收斂並且得到正確的預測結果，這部分將在後面補充