四柱漢諾塔問題

首先我們先回憶一下經典的漢諾塔問題：
問題描述
相傳在古印度聖廟中，有一種被稱為漢諾塔(Hanoi)的遊戲。該遊戲是在一塊銅板裝置上，有三根杆(編號A、B、C)，在A杆自下而上、由大到小按順序放置64個金盤(如下圖)。遊戲的目標：把A杆上的金盤全部移到C杆上，並仍保持原有順序疊好。操作規則：每次只能移動一個盤子，並且在移動過程中三根杆上都始終保持大盤在下，小盤在上，操作過程中盤子可以置於A、B、C任一杆上。

既然都介紹了，我們就來寫一下這個三柱漢諾塔問題的一個核心程式碼吧

void move(int i,int j)
{
	cout << i <<
 
 " -> " << j << endl;
	num ++ ;
}

void hanoi(int n,int a,int b,int c)
{
	if(n == 0)
		return;
	else{
		hanoi(n - 1,a,c,b);
		move(a,c);
		hanoi(n - 1,b,a,c);
	}
}

好了，我們介紹一下四柱漢諾塔問題。其實問題很簡單，就是再加一根柱子，把A上的盤子，經過B和C移動到D上去。

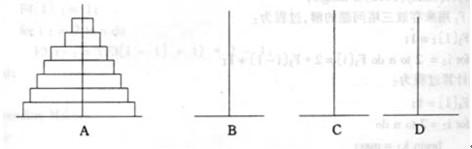
分析
將k個盤子先從A上經過C，D移動到B上去，然後再將下面n-k個盤子經過C移動到D上去，
再將之前的k個盤子經過A，C移動到D上去，完成。
我們採用動態規劃

dp[i] = pow(2, i - j) - 1 + 2 * dp[j];從j處斷開 j <= i

即先把j個盤子做一次四柱漢諾塔，再把i-j個盤子做一次三柱漢諾塔，再把j個盤子做一次四柱漢諾塔。
(其中pow(2, i - j) - 1的意思是i-j個盤子用三個柱子移動時的次數，是固定的)

/*
n個盤子的四柱漢諾塔問題
*/
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
 


#define MAX_N 63
#define INF 0x3f3f3f3f


using namespace std;

int dp[MAX_N];
int num;

void move(char a,char b)
{
	printf("%c --> %c\n", a, b);
	num++;
}


int find_hanoi(int n,int &k)
{
	num = 0;
	dp[1] = 1;
	dp[2] = 3;
	for (int i = 3; i <= n; i++)
	{
		for (int j = 1; j < i; j++)
		{
			long long t = pow(2, i - j) - 1 + 2 * dp[j];

			if (t < dp[i] || !dp[i])
			{
				dp[i] = t;
				k = j;

			}
		}
	}
	return dp[n];
}
int main()
{
	int n;
	int k = 0;
	cout << "請輸入盤子的數目n" << endl;
	memset(dp, 0, sizeof(dp));
	cin >> n;
	cout << "移動" << n << "個盤子最少需要的次數為：" << find_hanoi(n, k) << endl;
	cout << "斷開位置：" << k << endl;
	
	return 0;
}

下面的程式碼就加了一個內容，輸出移動次序，並且驗證結果是否正確。
其中我們利用了動態規劃的演算法，計算出了n個盤子的情況下最優的斷開位置

/*
n個盤子的四柱漢諾塔問題
*/
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>

#define MAX_N 63
#define INF 0x3f3f3f3f


using namespace std;

int dp[MAX_N];
int num = 0;
int myfind[MAX_N];

int find_hanoi(int n)
{
	num = 0;
	dp[1] = 1;
	dp[2] = 3;
	for (int i = 3; i <= n; i++)
	{
		for (int j = 1; j < i; j++)
		{
			long long t = pow(2, i - j) - 1 + 2 * dp[j];

			if (t < dp[i] || !dp[i])
			{
				dp[i] = t;
				myfind[i] = j;

			}
		}
	}
	return dp[n];
}

void move(char i,char j)
{
	cout << i << " -> " << j << endl;
	num ++ ;
}

void hanoi03(int n,int a,int b,int c)
{
	if(n == 0)
		return;
	else{
		hanoi03(n - 1,a,c,b);
		move(a,c);
		hanoi03(n - 1,b,a,c);
	}
}

void hanoi04(int n, int k,int a,int b,int c,int d)
{

	if(n == 1){
		move(a,d);
		return;
	}
	if(n == 2){
		move(a,c);
		move(a,d);
		move(c,d);
		return;
	}
	if(k == 0)
		return;
	hanoi04(k,myfind[k],a,c,d,b);
	hanoi03(n-k,a,c,d);
	hanoi04(k,myfind[k],b,a,c,d);
	
}

int main()
{
	int n;
	int k = 0;
	char a = 'A';
	char b = 'B';
	char c = 'C';
	char d = 'D';
	memset(dp, 0, sizeof(dp));
	memset(myfind,0,sizeof(myfind));
	cout << "請輸入盤子的數目n" << endl;
	cin >> n;
	int index = find_hanoi(n);
	cout << "移動" << n << "個盤子最少需要的次數為：" << index << endl;
	cout << "移動次序****" << endl;
	hanoi04(n,myfind[n],a,b,c,d); 
	if(num == index){
		cout << "驗證正確" << endl;
	}
	return 0;
}