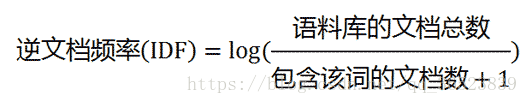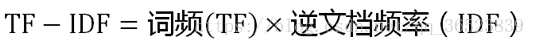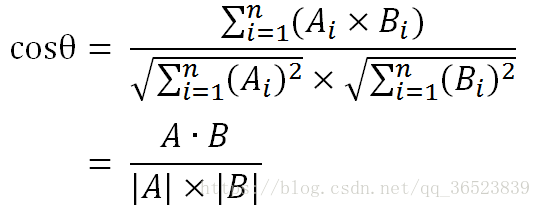TF-IDF及相關知識(餘弦相似性)
自然語言的處理是一個神奇的領域,它涉及到資料探勘、文字處理、資訊檢索等很多計算機前沿領域,由於複習相關知識,所以這裡對該方向的部分知識做一個簡單的介紹和記錄。
該文主要記錄的是一個很簡單卻很經典有效的演算法——TF-IDF。從它的概念到運算可能花不了10分鐘就能瞭解,並且用到的運算知識都不涉及高等數學,但往往能返回我們一個滿意的答案。
當我們輸入一段檢索資訊時,可以利用TF-IDF演算法,給我們返回一篇與我們搜尋比較符合的文章,下面對它做詳細介紹:
TF(詞頻):
TF-IDF的第一個知識點,TF(Term Frequency,縮寫為TF)表示詞頻,簡單點說就是某個單詞出現的頻率,這是很容易理解的,如果我們要知道某個詞是否是重要關鍵字,那麼很容易想到的就是計算該詞出現的數量。藉由阮老師使用的例子來說明:《中國蜜蜂養殖》一文中,出現最多的一些詞語可能是中國、蜜蜂、養殖,那麼統計這些單詞的個數(或者再做一些處理)就是該詞的頻率。
停用詞:
停用詞一個很簡單的常識概念。我們知道絕大多數文章中(的、了、是、在)等詞是最為常見的字詞,由此若我們直接統計關鍵詞的數量,那麼獲得的答案可能是無意義的,對於這些相當普通的詞語我們稱之為停用詞,在我們處理文章時極有可能需要先將這些詞語排除掉,預處理後再對文章做一個運算。停用詞表有很多,很多公司企業研究機構都製作有停用詞表,可以選擇使用。
IDF(逆文件頻率):
第二個知識點IDF,IDF(Inverse Document Frequency,縮寫為IDF)表示逆文件頻率。接著上面的例子來說,如果一文中中國、蜜蜂、養殖出現的次數一樣多,那是不是它們同等重要呢?很有可能不是,仔細想想,一篇文章出現(中國)的概率和出現(蜜蜂)的概率哪個大,可能很多文章中都會出現中國一詞,所以如果某個詞比較少見,但是它在這篇文章中多次出現,那麼它很可能就反映了這篇文章的特性,正是我們所需要的關鍵詞。於此我們需要一個數值(權重)來表示這些詞語的一個重要性,最常見的(的、了、是、在)等詞將給予最小的權重,較常見的(中國)等給予較小的權重,而(蜜蜂、養殖)這樣的詞語給予較大的權重,這個權重就叫做逆文件頻率,值大小與常見程度成反比。
有了上面的概念,下面說說具體的運算:
一、TF(詞頻)的幾種運算方式:
1:
2:
3:
以上的計算有多種(截圖來自阮老師的文章),可以考慮到實際的情況來採用,比如考慮到文章有長短之分,便於不同文章之間的比較,可以進行詞頻的”標準化“,即採用2來表示。
二、IDF(逆文件頻率):
由於前面對IDF的介紹,所以我們知道需要有一個包含很多文件的語料庫(如:corpus),來模擬語言的使用環境。
從該公式中可以很清楚的瞭解到如果一個詞越常見(包含該詞的文件數越多)則分母越大越接近0,對應的IDF越小。+1是為了避免分母為0。
三、TF-IDF:
最後結合兩者做一個運算,得到TF-IDF值。TF-IDF與一個詞在文件中的出現次數成正比,與該詞在整個語言中的出現次數成反比。最後對結果排序,選出最大的k個值,對應的關鍵詞就是運算的結果。
優缺點:
TF-IDF演算法的優點是運算簡單快速,比較符合實際情況。缺點是單純以一個“詞頻”衡量一個詞的重要性,不夠全面,比如:重要的詞可能出現的次數不多;可能位置資訊更重要,在第一段或每段第一句更為重要,不能視為同等重要(一種解決方法是對這些重要的位置賦予更高的權重)
餘弦相似性:
前面介紹了TF-IDF,下面介紹一種可以對文章之間相似性做運算的計算方式——餘弦相似性,通過該計算方式,我們可以對不同文章之間的相似性做一個定量的分析表示。
餘弦相似度的計算可以看成為兩個向量之間的運算,計算兩個向量之間的夾角,比較夾角時一般指兩者方向上的差別。當夾角為0,則兩者方向相同,向量重合;當夾角為90,則兩者垂直,方向完全無關;當夾角為180,則兩者方向相反。
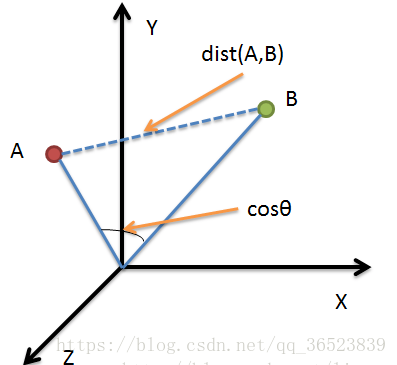
樣例示圖(來自):
圖中A、B兩點,若要計算兩點之間的距離則可以使用歐氏距離等方法計算,若計算A、B向量之間的相似度,則可以使用餘弦相似度來計算(歐氏距離表示點之間的距離,餘弦相似度表示變化趨勢相似度)。
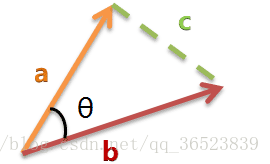
餘弦定理:
若a向量為[x1,y1],b向量為[x2,y2],所以上面的餘弦公式可以轉換為:
餘弦公式同樣適用於n維向量,如a為[x1,x2,x3,x4....x100],所以可以得出下面的公式:
餘弦值越接近1,就表明夾角越接近0度,也就是兩個向量越相似,這就叫"餘弦相似性"。
通過上面TF-IDF於餘弦相似度的學習後(TF-IDF計算一篇文章,餘弦相似度比較多篇),可以得出一種“尋找相似文章”的演算法:
- 使用TF-IDF演算法,找出兩篇文章各自的關鍵詞;
- 每篇文章各取出若干個關鍵詞(比如20個),合併成一個集合,計算每篇文章對於這個集合中的詞的詞頻(為了避免文章長度的差異,可以使用相對詞頻);
- 生成兩篇文章各自的詞頻向量;
- 計算兩個向量的餘弦相似度,值越大就表示越相似。