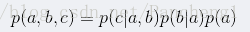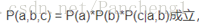貝葉斯網路(belief network)及相關知識整理
貝葉斯網路(belief network)及相關知識
頻率派:認為theta是個固定的未知常數。認為樣本是隨機的,重點研究樣本分佈
貝葉斯派:認為theta是不確定的未知數。認為樣本是固定的,重點研究引數theta的分佈
貝葉斯的思考方式不同於傳統“非黑即白,非0即1”的思考方式。
先驗分佈+樣本資訊=後驗分佈
有一個基本的先驗分佈,根據樣本資訊的變化和不斷迭代,得到被影響的後驗結果
條件概率:P(A|B)=P(A交B)/P(B)
聯合概率:P(A交B)=P(A,B)
邊緣概率:P(A),P(B)
貝葉斯公式:P(A|B)= P(B|A)P(A)/P(B)
——————————————————————————————————
貝葉斯網路(Bayesian network),又稱信念網路(Belief Network),或有向無環圖模型(directedacyclic graphical model),是一種概率圖模型是一種模擬人類推理過程中因果關係的不確定性處理模型,其網路拓樸結構是一個有向無環圖(DAG)。
“有環的話,謊言傳到最後自己都相信了”
貝葉斯網路的有向無環圖中的節點表示隨機變數,它們可以是可觀察到的變數,或隱變數、未知引數等。認為有因果關係(或非條件獨立)的變數或命題則用箭頭來連線。若兩個節點間以一個單箭頭連線在一起,表示其中一個節點是“因(parents)”,另一個是“果(children)”,兩節點就會產生一個條件概率值。
連線兩個節點的箭頭代表此兩個隨機變數是具有因果關係,或非條件獨立。
假設節點E直接影響到節點H,即E→H,則用從E指向H的箭頭建立結點E到結點H的有向弧(E,H),權值(即連線強度)用條件概率P(H|E)來表示:
把某個研究系統中涉及的隨機變數,根據是否條件獨立繪製在一個有向圖中,就形成了貝葉斯網路。
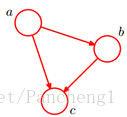
下圖是一個簡單的貝葉斯網路:
因為a導致b,a和b導致c,所以有聯合概率為:
貝葉斯網路的3種結構形式:
先引入D-分離(D-Separation)的概念:是一種用來判斷變數是否條件獨立的圖形化方法。即對於一個DAG(有向無環圖)E,D-Separation方法可以快速的判斷出兩個節點之間是否是條件獨立的。
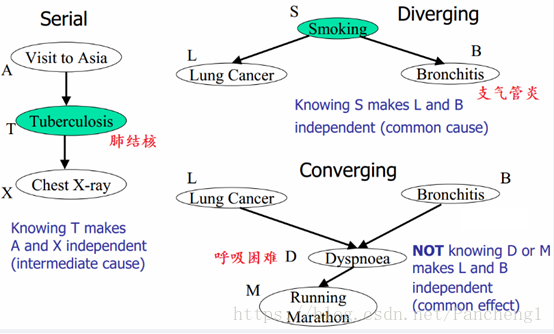
形式1:head-to-head
貝葉斯網路的第一種結構形式:
在c未知的條件下,a、b被阻斷(blocked),是獨立的,稱之為head-to-head條件獨立。
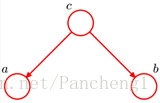
形式2:tail-to-tail
在c給定的條件下,a,b被阻斷(blocked),是獨立的,稱之為tail-to-tail條件獨立
形式3:head-to-tail
在c給定的條件下,a,b被阻斷(blocked),是獨立的,稱之為head-to-tail條件獨立。
當前狀態只跟上一狀態有關,跟上上或上上之前的狀態無關。這種順次演變的隨機過程,就叫做馬爾科夫鏈(Markov chain)。
——————————————————————————————————
因子圖是什麼?
為什麼要引入因子圖?
因子圖如何使用?
因子圖:
wikipedia上是這樣定義因子圖的:將一個具有多變數的全域性函式因子分解,得到幾個區域性函式的乘積,以此為基礎得到的一個雙向圖叫做因子圖(Factor Graph)。包含變數節點和函式節點。
頂點是這兩種中的一種邊表示其函式關係。
一個全域性函式通過因式分解能夠分解為多個區域性函式的乘積,這些區域性函式和對應的變數關係就體現在因子圖上。
因子圖是概率圖中的一種。其他概率圖如貝葉斯圖、貝葉斯網路、馬爾科夫隨機場都是概率圖。
有向圖vs無向圖vs條件隨機場:
1.有向圖模型(Directed Graphical Models, DGM),又稱作貝葉斯網路:
2. 無向圖模型(UndirectedGraphical Models, UGM), 又被稱為馬爾科夫隨機場或者馬爾科夫網路:
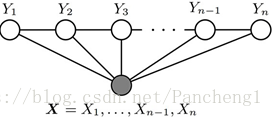
3. 設X=(X1,X2…Xn)和Y=(Y1,Y2…Ym)都是聯合隨機變數,若隨機變數Y構成一個無向圖 G=(V,E)表示的馬爾科夫隨機場(MRF),則條件概率分佈P(Y|X)稱為條件隨機場(Conditional Random Field, CRF)。如下圖所示為一個線性鏈條件隨機場的無向圖模型:
邊緣分佈:多維隨機變數中,只包含其中部分變數的概率分佈。
*****【實際問題—(抽象)—概率圖——因子圖——sum-product求解變數的邊緣分佈】
在概率圖中,求某個變數的邊緣分佈是常見的問題。這問題有很多求解方法,其中之一就是把貝葉斯網路或馬爾科夫隨機場轉換成因子圖,然後用sum-product演算法求解。換言之,基於因子圖可以用sum-product演算法高效的求各個變數的邊緣分佈。
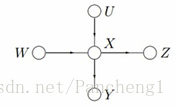
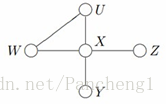
由貝葉斯網路構造因子圖的方法:
· 貝葉斯網路中的一個因子對應因子圖中的一個結點
· 貝葉斯網路中的每一個變數在因子圖上對應邊或者半邊
· 結點g和邊x相連當且僅當變數x出現在因子g中。
如何由聯合概率分佈求邊緣概率分佈:
· 聯合概率表示兩個事件共同發生的概率。A與B的聯合概率表示P(A,B)。
· 邊緣概率(又稱先驗概率)是某個事件發生的概率。求邊緣概率:在聯合概率中,把最終結果中不需要的那些事件合併成其事件的全概率而消失(對離散隨機變數用求和得全概率,對連續隨機變數用積分得全概率)。這稱為邊緣化(marginalization)。A的邊緣概率表示為P(A),B的邊緣概率表示為P(B)。
某個隨機變數fk的邊緣概率可由x1,x2,x3, ..., xn的聯合概率求到,具體公式為:
變數的邊緣概率等於所有與他相連的函式傳遞過來的訊息的積。
計算過程將一個概率分佈寫成兩個因子的乘積,而這兩個因子可以繼續分解或者通過已知得到。這種利用訊息傳遞的觀念計算概率的方法便是sum-product演算法。前面說過,基於因子圖可以用sum-product演算法可以高效的求各個變數的邊緣分佈。
sum-product演算法,也叫beliefpropagation,有兩種訊息:
一種是變數(Variable)到函式(Function)的訊息,


另外一種是函式(Function)到變數(Variable)的訊息,

如果因子圖是無環的,則一定可以準確的求出任意一個變數的邊緣分佈,如果是有環的,則無法用sum-product演算法準確求出來邊緣分佈。
例:貝葉斯網路
對應的因子圖:
··········受益良多·······
轉自:https://blog.csdn.net/bluebelfast/article/details/51509223