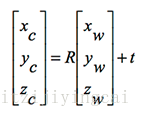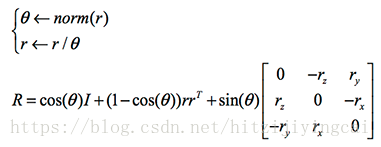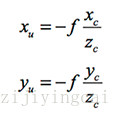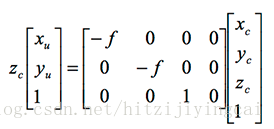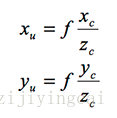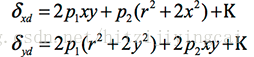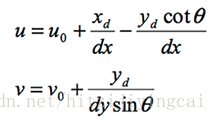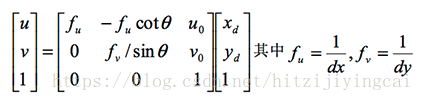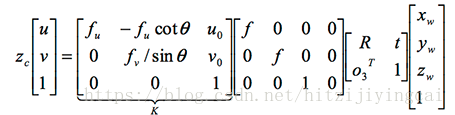在機器視覺領域，相機的標定是一個關鍵的環節，它決定了機器視覺系統能否有效的定位，能否有效的計算目標物。相機的標定基本上可以分為兩種，第一種是相機的自標定；第二種是依賴於標定參照物的標定方法。前者是相機拍攝周圍物體，通過數字影象處理的方法和相關的幾何計算得到相機引數，但是這種方法標定的結果誤差較大，不適合於高精度應用場合。後者是通過標定參照物，由相機成像，並通過數字影象處理的方法，以及後期的空間算術運算計算相機的內參和外參。這種方法標定的精度高，適用於對精度要求高的應用場合,本文主要針對後者進行描述。

標定的概念：在影象測量過程以及機器視覺應用中，為確定空間物體表面某點的三維幾何位置與其在影象中對應點之間的相互關係，必須建立相機成像的幾何模型，這些幾何模型引數就是相機引數。在大多數條件下這些引數必須通過實驗與計算才能得到，這個求解引數（內參、外參、畸變引數）的過程就稱之為相機標定（或攝像機標定）。無論是在影象測量或者機器視覺應用中，相機引數的標定都是非常關鍵的環節，其標定結果的精度及演算法的穩定性直接影響相機工作產生結果的準確性。因此，做好相機標定是做好後續工作的前提，提高標定精度是科研工作的重點所在。畸變（distortion）是對直線投影（rectilinear projection）的一種偏移。簡單來說直線投影是場景內的一條直線投影到圖片上也保持為一條直線。畸變簡單來說就是一條直線投影到圖片上不能保持為一條直線了，這是一種光學畸變（optical aberration）,可能由於攝像機鏡頭的原因。

相機在計算機視覺應用中起著重要作用，作為影象資料來源，影響著後續各個處理步驟。成像模型就是用數學公式刻畫整個成像過程，即被拍攝物體空間點到照片成像點之間的幾何變換關係。

總體上，相機成像可以分為四個步驟：剛體變換、透視投影、畸變校正和數字化影象。

一、剛體變換（從世界座標系到相機座標系）

世界座標系（world coordinate）(xw,yw,zw)，也稱為測量座標系，是一個三維直角座標系，以其為基準可以描述相機和待測物體的空間位置。世界座標系的位置可以根據實際情況自由確定。

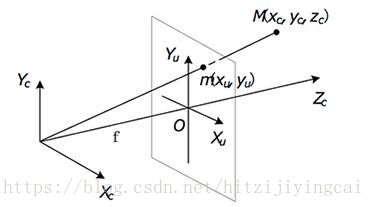
相機座標系（camera coordinate）(xc,yc,zc)，也是一個三維直角座標系，原點位於鏡頭光心處，x、y軸分別與相面的兩邊平行，z軸為鏡頭光軸，與像平面垂直。

剛體變換隻改變物體的空間位置(平移)和朝向(旋轉)，而不改變其形狀，可用兩個變數來描述：旋轉矩陣R和平移向量t：

齊次座標下可寫為：

旋轉矩陣R是正交矩陣，可通過羅德里格斯（Rodrigues）變換轉換為只有三個獨立變數的旋轉向量：

因此，剛體變換可用6個引數來描述，這6個引數就稱為相機的外參(Extrinsic)，相機外參決定了空間點從世界座標系轉換到相機座標系的變換，也可以說外參描述了相機在世界座標系中的位置和朝向。

二、透視投影（從相機座標系到影象座標系）

我們可以將透鏡的成像簡單地抽象成下圖所示：

設 f=OB 表示透鏡的焦距，m=OC 為像距，n=AO 為物距，有：

一般地，由於物距遠大於焦距，即 n>>f，所以 m≈f，此時可以用小孔模型代替透鏡成像：

可得：

齊次座標下有：

如果將成像平面移到相機光心與物體之間，則有中心透視模型：

可得：

齊次座標下有：

總體上看，透視投影將相機座標系中的點投影到理想影象座標系，其變換過程只與相機焦距 f 有關。

三、畸變矯正

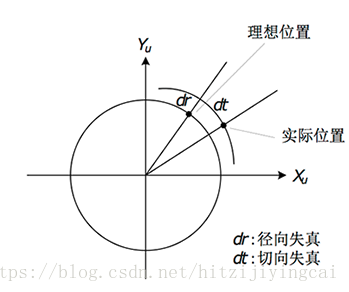
理想的針孔成像模型確定的座標變換關係均為線性的，而實際上，現實中使用的相機由於鏡頭中鏡片因為光線的通過產生的不規則的折射，鏡頭畸變（lens distortion）總是存在的，即根據理想針孔成像模型計算出來的像點座標與實際座標存在偏差。畸變的引入使得成像模型中的幾何變換關係變為非線性，增加了模型的複雜度，但更接近真實情形。畸變導致的成像失真可分為徑向失真和切向失真兩類：

畸變型別很多，總體上可分為徑向畸變和切向畸變兩類，徑向畸變的形成原因是鏡頭製造工藝不完美，使得鏡頭形狀存在缺陷，包括枕形畸變和桶形畸變等，可以用如下表達式來描述：

切向畸變又分為薄透鏡畸變和離心畸變等，薄透鏡畸變則是因為透鏡存在一定的細微傾斜造成的；離心畸變的形成原因是鏡頭是由多個透鏡組合而成的，而各個透鏡的光軸不在同一條中心線上。切向畸變可以用如下數學表示式來描述：

在引入鏡頭的畸變後，成像點從理想影象座標系到真實影象座標系的變換關係可以表示為：

實際計算過程中，如果考慮太多高階的畸變引數，會導致標定求解的不穩定。

四、數字化影象

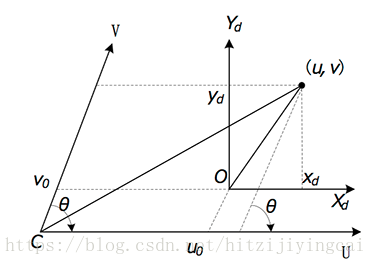
光線通過相機鏡頭後最終成像在感光陣列(CCD或CMOS)上，然後感光陣列將光訊號轉化為電訊號，最後形成完整的影象。我們用dx和dy分別表示感光陣列的每個點在x和y方向上物理尺寸，即一個畫素是多少毫米，這兩個值一般比較接近，但由於製造工藝的精度問題，會有一定誤差，同樣的，感光陣列的法向和相機光軸也不是完全重合，即可以看作成像平面與光軸不垂直。

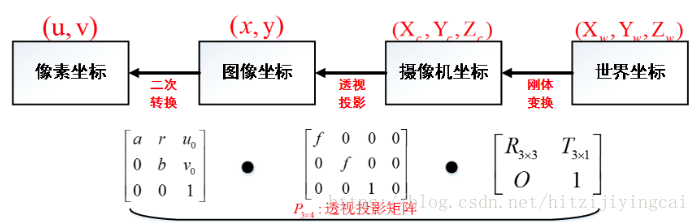
我們用仿射變換來描述這個過程，如上圖，O點是影象中心點，對應影象座標(u0，v0)，Xd - Yd是真實影象座標系，U-V是數字化影象座標系，有：

齊次座標下有：

上式中的變換矩陣即為相機的內參數矩陣 K，其描述了相機座標系中點到二維影象上點的變換過程。

綜上所述，在不考慮鏡頭畸變的情況下，相機的整個成像過程可表示為：

四個座標系之間存在著下述關係 ( 矩陣依次左乘 ):

五、引數標定

引數標定即通過一定方法求得上述成像模型中的各個未知量（5個內參、6個外參以及畸變引數）。相機標定主要有傳統標定方法和自標定方法兩類，傳統標定方法需要標定參照物，參照物的引數已知，然後分析拍攝到的參照物影象，求得相機引數，如直接線性變換(DLT)方法、Tsai兩步標定法和張正友平面標定法等。傳統方法操作相對複雜，但精度較高。

自標定方法不需要標定參照物，只需要多幅影象點的對應關係就能求解出相機引數，如基於無窮遠平面、絕對二次曲面的自標定方法、基於Kruppa方程的自標定方法等。自標定方法靈活方便，但由於是非線性標定，精度和魯棒性都不高。

這裡主要介紹張正友平面標定法，其操作相對簡單，且精度較高，實際應用中很常用。

整個標定過程包括如下步驟：

• 列印一張棋盤格，把它貼在一個平面上，作為標定物。
• 通過調整標定物或攝像機的方向，為標定物拍攝一些不同方向的照片。
• 從照片中提取棋盤格角點。
• 估算理想無畸變的情況下，五個內參和六個外參。
• 應用最小二乘法估算實際存在徑向畸變下的畸變係數。
• 極大似然法，優化估計，提升估計精度。

首先是準備資料，本人的資料示例如圖：

1、MATLAB相機標定

實際應用中，常使用MATLAB標定工具箱進行相機標定 Camera Calibration Toolbox for Matlab，只需匯入拍攝的棋盤格照片，輸入一些引數，然後對每張照片選擇棋盤區域，就可以自動完成整個標定過程，並得到視覺化的標定結果。

• 開啟matlab，找到“Camera Calibrator”並開啟

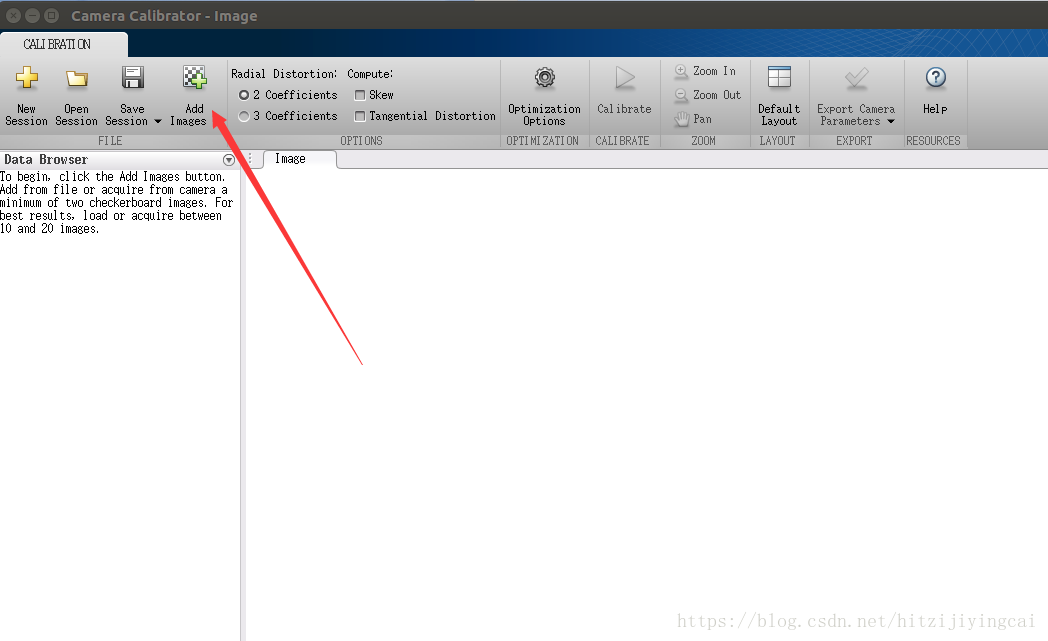
• 在新視窗中選擇新增圖片“Add Images”

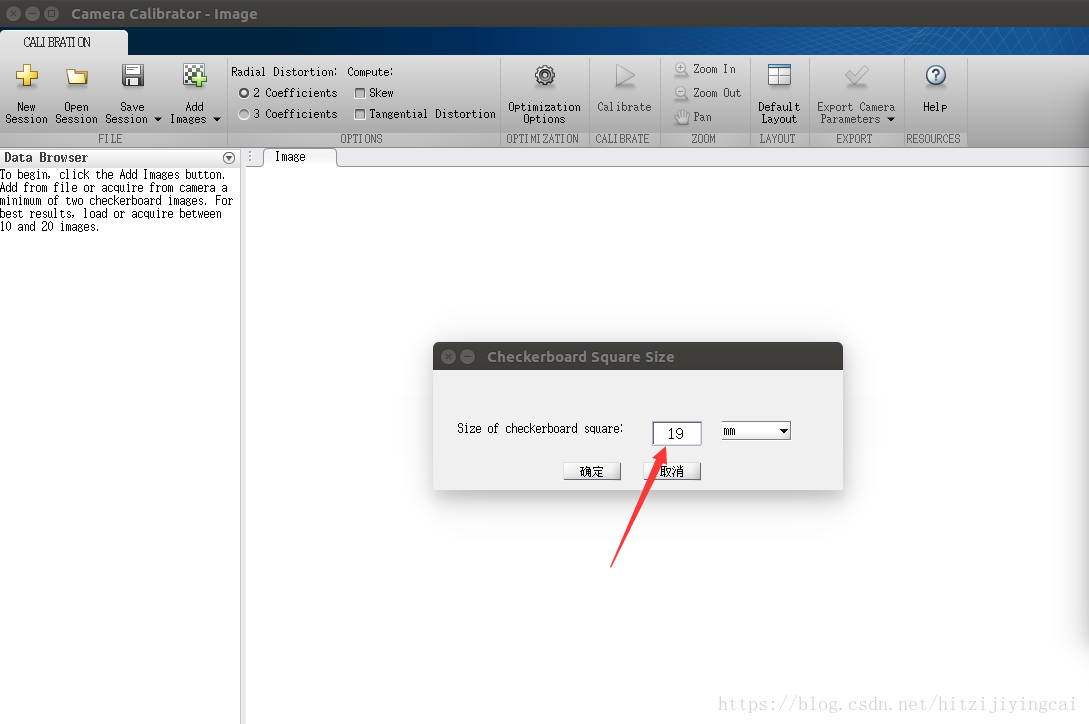
• 新增圖片之後，會有如下提示，設定棋盤格的實際大小之後，點選ok

注意，假如在採集圖片時角度均較好，則可以順利進行下一步，但是本人咋實驗時，由於採集的圖片有幾張角度不太好，因此在這一步之後出現了一個提示，是說有幾張圖片棄用了，若出現了可以不用管它，但是可以看一下都有哪幾張圖片棄用了。

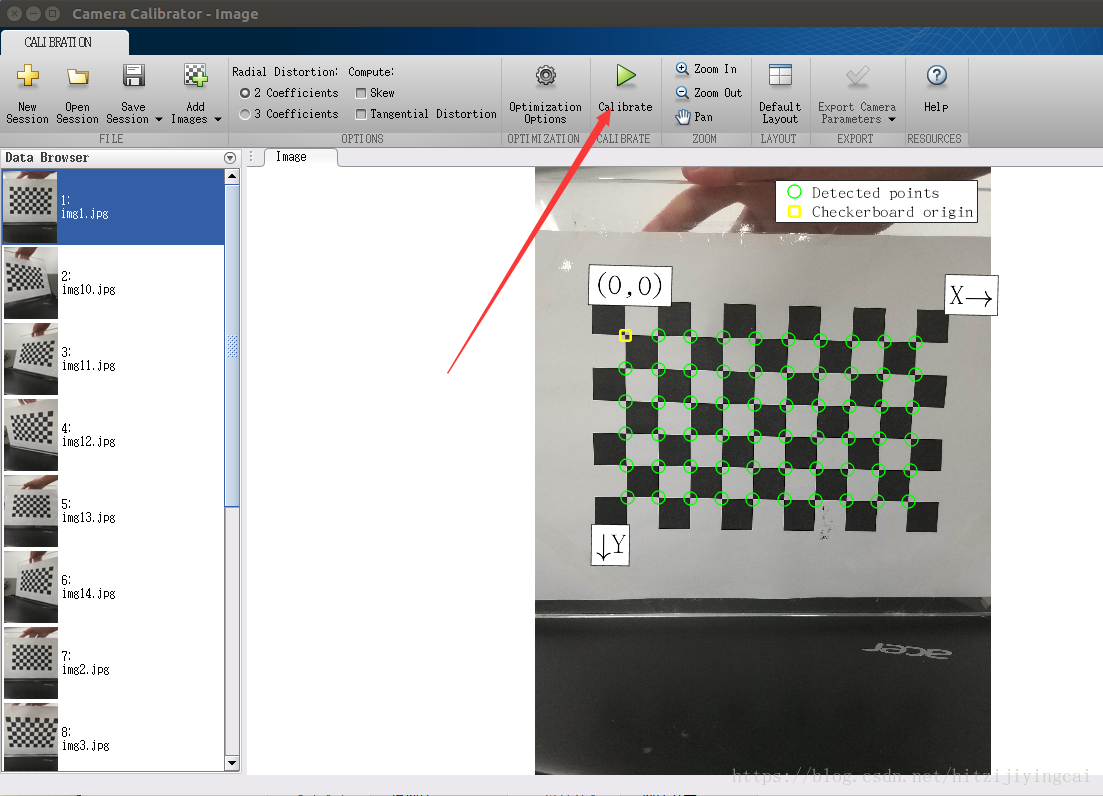
• 點選“Calibrate”開始計算

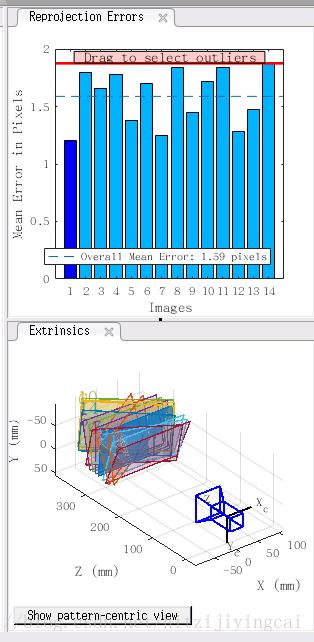
點選完成計算之後，可以在右側看到如圖：

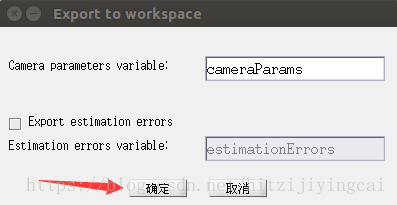
• 點選“Export Camera Parameters”，輸出到matlab命令視窗

• 匯出的資料如下：

• 在命令視窗輸入以下命令即可獲得內參矩陣和徑向畸變：

2、opencv-python 張正友相機標定法實現

import cv2
import glob
import numpy as np
'''
cbraw和cbcol是我自己加的。tutorial用的棋盤足夠大包含了7×6以上
個角點，我自己用的只有6×4。這裡如果角點維數超出的話，標定的時候會報錯。
'''
cbraw = 6
cbcol = 4
# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((cbraw*cbcol,3), np.float32)
'''
設定世界座標下點的座標值，因為用的是棋盤可以直接按網格取；
假定棋盤正好在x-y平面上，這樣z值直接取0，簡化初始化步驟。
mgrid把列向量[0:cbraw]複製了cbcol列，把行向量[0:cbcol]複製了cbraw行。
轉置reshape後，每行都是4×6網格中的某個點的座標。
'''
objp[:,:2] = np.mgrid[0:cbraw,0:cbcol].T.reshape(-1,2)

objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
#glob是個檔名管理工具
images = glob.glob("/home/hqd/桌面/c1/*.jpg")
for fname in images:
#對每張圖片，識別出角點，記錄世界物體座標和影象座標
    img = cv2.imread(fname) #source image
    #我用的圖片太大，縮小了一半
    img = cv2.resize(img,None,fx=0.5, fy=0.5, interpolation = cv2.INTER_CUBIC)
    gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) #轉灰度
    #cv2.imshow('img',gray)
    #cv2.waitKey(1000)
    #尋找角點，存入corners，ret是找到角點的flag
    ret, corners = cv2.findChessboardCorners(gray,(6,4),None)
    #criteria:角點精準化迭代過程的終止條件
    criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
    #執行亞畫素級角點檢測
    corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)

    objpoints.append(objp)
    imgpoints.append(corners2)
    #在棋盤上繪製角點,只是視覺化工具
    img = cv2.drawChessboardCorners(gray,(6,4),corners2,ret)
    cv2.imshow('img',img)
    #cv2.waitKey(1000)
'''
傳入所有圖片各自角點的三維、二維座標，相機標定。
每張圖片都有自己的旋轉和平移矩陣，但是相機內參和畸變係數只有一組。
mtx，相機內參；dist，畸變係數；revcs，旋轉矩陣；tvecs，平移矩陣。
'''
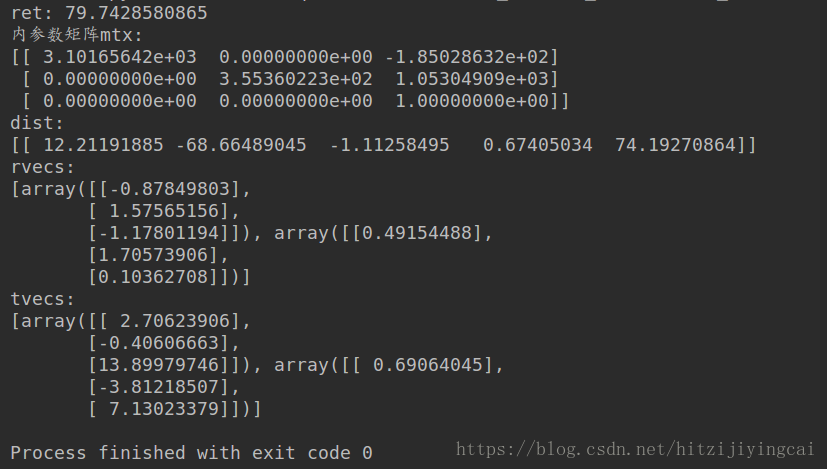
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)

print "ret:",ret
print "內參數矩陣mtx:\n",mtx        # 內參數矩陣
print "dist:\n",dist      # 畸變係數   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print "rvecs:\n",rvecs    # 旋轉向量  # 外引數
print "tvecs:\n",tvecs    # 平移向量  # 外引數

在用前面的資料圖片進行實驗得到的結果為：

NB：關於相機標定，還有使用vs+opencv的方法，在本人實踐後再更新

參考資料：