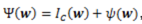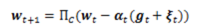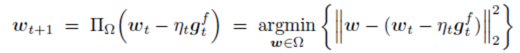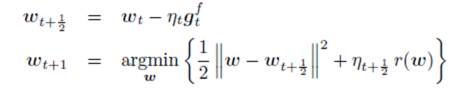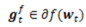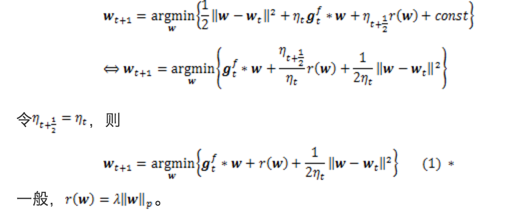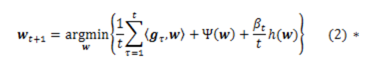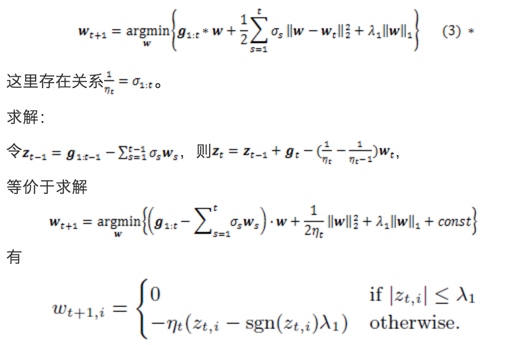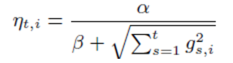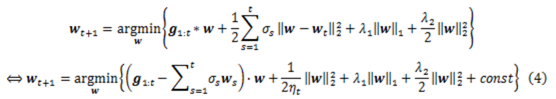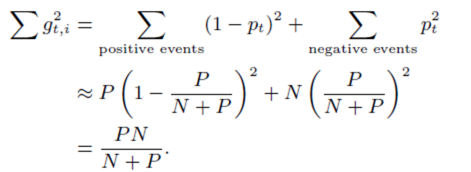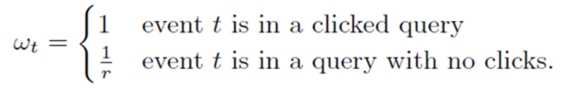現在特別是像做線上學習和CTR這塊，應用LR是最廣泛的。但是批量處理超大規模的資料集和線上資料流時就遇到了問題，FTRL就是google在這樣的背景下研發出來的。在處理非光滑正則化項的凸優化問題上效能非常出色，目前現在阿里也是已經在應用到實際的產品中去了。

      當時Google在2013年KDD上發表了FTRL演算法後，在業界引起了巨大的反響，國內外各大IT公司紛紛上線該演算法。Amazon在他們的搜尋廣告中上線該演算法取得了不錯的效果；Yahoo在新聞推薦中也有嘗試該演算法；國內網易、搜狐、新浪、百度都有上線該演算法，也都取得了不錯效果；我們目前多個團隊也都上線線上學習系統，並取得不錯的業務效果。

      批處理bacth的離線機器學習方法在每次迭代計算的過程中，需要把全部的訓練資料載入到記憶體中計算（例如計算全域性梯度）， 雖然有分散式大規模的機器學習平臺，在某種程度上批處理方法對訓練樣本的數量還是有限制的，onlinelearning不需要cache所有資料，以流式的處理方式可以處理任意數量的樣本。研究onlinelearning有兩個角度，線上凸優化和線上Bayesian。

      線上凸優化方法有很多，像FOBOS演算法、RDA、FTRL等；線上Bayesian 方面有比如AdPredictor 演算法、基於內容的線上矩陣分解演算法等，有興趣的可以多瞭解下。包括我們在實際專案中會將FTRL做相應的改進優化，KDD競賽也是用的FTRL不少。

今天主要介紹三塊內容：

1.傳統的批量演算法、線上學習演算法；

2.簡單介紹下SGD、FOBOS、RDA等演算法；

3.FTRL、FTRL-Proximal的工程實現。

Part 1：

Online learning定義： Online learning主要指每次來一個樣本，利用一個迭代方法更新模型變數，使得當前期望loss最小。

傳統演算法特點： 【傳統Batch演算法】

批量演算法中每次迭代對全體訓練資料集進行計算（例如計算全域性梯度），優點是精度和收斂還可以，缺點是無法有效處理大資料集（此時全域性梯度計算代價太大），且沒法應用於資料流做線上學習。

【傳統線上演算法，例如SGD】

線上學習演算法的特點是：每來一個訓練樣本，就用該樣本產生的loss和梯度對模型迭代一次，一個一個數據地進行訓練，因此可以處理大資料量訓練和線上訓練。常用的有線上梯度下降（OGD）和隨機梯度下降（SGD）等，本質思想是對上面【問題描述】中的未加和的單個數據的loss函式 L（w，zi)做梯度下降，因為每一步的方向並不是全域性最優的，所以整體呈現出來的會是一個看似隨機的下降路線。

梯度下降類的方法的優點是精度確實不錯，但是不足相關paper主要提到兩點：

1、簡單的線上梯度下降很難產生真正稀疏的解，稀疏性在機器學習中是很看重的事情，尤其我們做工程應用，稀疏的特徵會大大減少predict時的記憶體和複雜度。這一點其實很容易理解，說白了，即便加入L1範數，因為是浮點運算，訓練出的w向量也很難出現絕對的零。到這裡，大家可能會想說，那還不容易，當計算出的w對應維度的值很小時，我們就強制置為零不就稀疏了麼。對的，其實不少人就是這麼做的，FOBOS都是類似思想的應用；

2、對於不可微點的迭代會存在一些問題，具體有什麼問題，有一篇paper是這麼說的：the iterates of the subgradient method are very rarely at the points of non-differentiability。

Part 2：

SGD：

對正則項Ψ(w)的一般表示：

，其中，Ic(w)是一個hard集合約束，ψ(w)是一個soft正則化。

SGD的迭代形式：

其中，α_t是步長，g_t是loss function的次梯度，ξ_(t )是ψ(w)的次梯度（subgradient）， Π_C是對約束集C的投影。 對次梯度不熟的可以檢視下wiki，主要用於處理函式的不可微點：http://zh.wikipedia.org/wiki/%E6%AC%A1%E5%AF%BC%E6%95%B0 SGD存在的問題上面主要列了1）精度低；2）收斂慢；3）幾乎得不到稀疏解。其中對online learning最重要的問題是SGD很難得到需要的正則化設計的解，特別是幾乎得不到稀疏解。

FOBOS：

FOBOS，2009年由Duchi（Berkeley）與Singer（google）[1]提出，對投影次梯度方法的一個改造。可以有效得到稀疏解。 投影次梯度方法的一般形式（與SGD幾乎一致）：

FOBOS的迭代將投影次梯度法拆成兩步：

 其中，

。第二步中，第一項保持新的解不要離第一步的臨時解太遠，第二項限制模型複雜度，即正則項，**用於產生稀疏解。** **為了得到後續統一的另一種表達，這裡做個簡單的推導：** 將迭代第一步帶入第二步中，FOBOS的迭代等價於：

註明：式（1）即為FOBOS的迭代形式，但是為何與總括表中第一行形式不同？而實際上兩種方式是等價的！

RDA：

RDA，2010微軟提出，特點：相對FOBOS，在精度與稀疏性之間做平衡，其中實驗表明，在L1正則下，RDA比FOBOS可以更加有效地得到稀疏解。 RDA的迭代：

收斂率與公式裡的引數有關。式（2）經過簡單的變化，可以得到總括表中的第三行。

Part 3：

首先感謝下H. Brendan McMahan搞了3年paper出來了，發展歷程和基本說明如下：

10年理論性paper，但未顯式地支援正則化項迭代；11年證明regret bound以及引入通用的正則化項；11年另一篇的paper揭示OGD、FOBOS、RDA等演算法與FTRL關係；13年的paper給出了工程性實現，並且附帶了詳細的虛擬碼，開始被大規模應用。

可以看作RDA和FOBOS的混合，但在L1範數或者其他非光滑的正則項下，FTRL比前兩者更加有效。

FTRL-Proximal，KDD 2013 google的論文，帶工程實現虛擬碼，相信當前online learning的實現大都是參照這邊paper來的。FTRL-Proximal，融合了RDA和FOBOS的特點，論文的實驗對比，在L1正則下，稀疏性與精度都好於RDA和FOBOS。 FTRL，即Follow The Regularized Leader。FTRL-Proximal的形式上與RDA只有第三項不同，如下，

這一個closed form解推導並不難，w分3種情況求解就行了。論文（John Duchi and Yoram Singer. E_cient learning using forward-backward splitting. In NIPS, 2009.）中對於各種norm下的下一個點closed form的解有詳細說明。

FTRL-Proximal對每次迭代的學習率做了一個優化，使得解的每一維的學習率不同，與統一的學習率相比，這種做法考慮了訓練樣本在不同特徵維度分佈的不均勻性。具體形式如下

FTRL-Proximal演算法：

偽碼採用的是L1和L2混合正則，即實際的迭代是如下形式：

FTRL-Proximal演算法的實現，基於式（4）。其中

， 是logistic regression的交叉熵loss function的梯度。

FTRL-Proximal工程實現上的tricks：

1.saving memory 方案1）Poisson Inclusion：對某一維度特徵所來的訓練樣本，以p的概率接受並更新模型。 方案2）Bloom Filter Inclusion：用bloom filter從概率上做某一特徵出現k次才更新。 2.浮點數重新編碼 1）特徵權重不需要用32bit或64bit的浮點數儲存，儲存浪費空間 2）16bit encoding，但是要注意處理rounding技術對regret帶來的影響 3.訓練若干相似model 1）對同一份訓練資料序列，同時訓練多個相似的model 2）這些model有各自獨享的一些feature，也有一些共享的feature 3）出發點：有的特徵維度可以是各個模型獨享的，而有的各個模型共享的特徵，可以用同樣的資料訓練。 4.Single Value Structure 1）多個model公用一個feature儲存（例如放到cbase或redis中），各個model都更新這個共有的feature結構 2）對於某一個model，對於他所訓練的特徵向量的某一維，直接計算一個迭代結果並與舊值做一個平均 5.使用正負樣本的數目來計算梯度的和（所有的model具有同樣的N和P）

6.subsampling Training Data

1）在實際中，CTR遠小於50%，所以正樣本更加有價值。通過對訓練資料集進行subsampling，可以大大減小訓練資料集的大小 2）正樣本全部採（至少有一個廣告被點選的query資料），負樣本使用一個比例r取樣（完全沒有廣告被點選的query資料）。但是直接在這種取樣上進行訓練，會導致比較大的biased prediction 3）解決辦法：訓練的時候，對樣本再乘一個權重。權重直接乘到loss上面，從而梯度也會乘以這個權重。

參考文獻 [1] John Duchi and Yoram Singer. E_cient learning using forward-backward splitting. In NIPS, 2009. [2] Lin Xiao. Dual averaging method for regularized stochastic learning and online optimization. In NIPS, 2010. [3] H. B. McMahan. Follow-the-regularized-leader and mirror descent: Equivalence theorems and L1 regularization. In AISTATS, 2011. [4] H. Brendan McMahan, Gary Holt, D. Sculley, Michael Young,Dietmar Ebner, Julian Grady,LanNie, Todd Phillips, Eugene Davydov,Daniel Golovin, Sharat Chikkerur, Dan Liu, Martin Wattenberg,Arnar Mar Hrafnkelsson, Tom Boulos, Jeremy Kubica. Ad Click Prediction: a View from the Trenches. KDD’13, August 11–14, 2013, Chicago, Illinois, USA.

原文連結：https://zhuanlan.zhihu.com/p/20447450